| > | restart:#"m13_p77" |
En un proyecto espacial, se pretende mantener un depósito de hidrógeno líquido (LH2), de modo pasivo sin pérdida de masa (i.e. sin vaporización), para lo cual se piensa situarlo detrás de un escudo radiativo que lo proteja del Sol y del resto de la nave (no se contemplan otros cuerpos). Considérese un depósito cilíndrico de 1,5 m de diámetro exterior y 5 m de longitud, a 0,25 m del escudo, que es un disco plano coaxial de 4,5 m de diámetro. El escudo estaría compuesto de varias capas aislantes y metalizadas, tal que la emisividad hacia el depósito puede suponerse =0,005. El depósito sería de 3 mm de espesor de aluminio A7075 (a 30 K su conductividad es k=40 W/(m·K)), conteniendo LH2 a 1 MPa (TELV=31 K), y llevaría una capa de 50 mm de espesor de espuma de poliuretano (k=0.007 W/(m·K) en vacío) con un recubrimiento reflectante solar de propiedades =0,1 y =0,9. Se estima que la unión estructural (tres tubos) del depósito con el resto de la nave introducirá una carga de 0,5 W por conducción térmica (se desprecian sus efectos radiativos). Se pide:
a) Razonar cuánto valdría el factor de vista del depósito (completo) al parasol, F12, en el caso límite de un parasol de diámetro mucho mayor que las dimensiones del depósito. Ya con las dimensiones dadas, razonar cuál será mayor, F12, o F21.
b) Para determinar F12, se va a calcular previamente los factores de vista de cada cara (base delantera, cara lateral, y base trasera) respecto al parasol. Determinar todos estos valores numéricos. Puede aproximarse el F1l,2 (i.e. desde la superficie lateral de 1, al 2) por el factor de vista bidimensional de la sección recta.
c) Con el modelo de cuerpos negros, plantear el balance energético general del depósito considerando toda su superficie exterior isoterma (T1), así como la del escudo (T2). Determinar T1 para mantener el régimen estacionario.
d) Determinar T2 con el modelo anterior.
e) Determinar T2 con las propiedades termo-ópticas reales dadas.
f) Calcular la carga térmica máxima terrestre que recibiría el depósito si estuviese en órbita geoestacionaria.
Datos:
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(h_>0,r>0):interface(displayprecision=2): |
| > | su:="H2":dat:=[D1=1.5*m_,L1=5*m_,Ls=0.25*m_,D2=4.5*m_,epsilon2=0.005,delta0=3e-3*m_,k0=30*W_/(m_*K_),pH=1e6*Pa_,TH=31*K_,delta1=0.05*m_,k1=0.007*W_/(m_*K_),alpha1=0.1,epsilon1=0.9,Qcond_sop=0.5*W_,Tinf=2.7*K_];dat:=op(dat),Const,SI2,SI1:Hdat:=get_liq_data(su),get_gas_data(su):get_pv_data(su): |
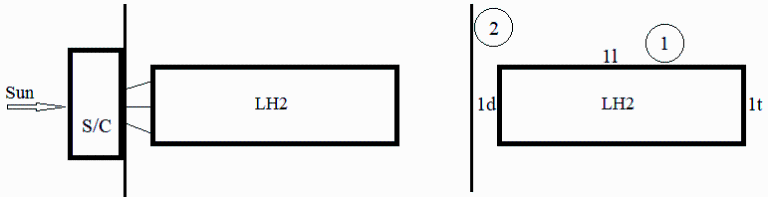
a) Razonar cuánto valdría el factor de vista del depósito (completo) al parasol, F12, en el caso límite de un parasol de diámetro mucho mayor que las dimensiones del depósito. Ya con las dimensiones dadas, razonar cuál será mayor, F12, o F21.
Sea A2 la superficie de la cara vista del parasol, A1 la superficie total del depósito, con 1d la cara delantera, 1l la lateral, y 1t la trasera. Supondremos que el depósito es un cilindro con bases planas (lo normal es que sean convexas). Si el escudo es infinito, F12=0,5 porque la mitad de lo que emita 1 irá a la izquierda y la otra mitad a la derecha. Por trozos, F1d2=1, F1l2=1/2, y F1t2=0, y la composición sería:
| > | eqF1d2:=F1d2=1;eqF1l2:=F1l2=1/2;eqF1t2:=F1t2=0;eqA1:=A1=A1d+A1l+A1t;eqF12:=F12=(A1d*F1d2+A1l*F1l2+A1t*F1t2)/A1;A1d=A1t;eqF12_:=subs(eqF1d2,eqF1l2,eqF1t2,eqA1,A1t=A1d,eqF12);simplify(%) |
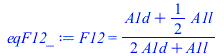 |
Si es finito, como se ha de verificar que A1·F12=A2·F21, basta comparar las áreas.
| > | eqA1d:=A1d=Pi*D1^2/4;eqA1d_:=evalf(subs(dat,%));eqA1l:=A1l=Pi*D1*L1;eqA1l_:=eval(subs(dat,%));eqA1:=A1=2*Pi*D1^2/4+Pi*D1*L1;eqA1_:=evalf(subs(dat,%));eqA2:=A2=Pi*D2^2/4;eqA2_:=evalf(subs(dat,%)); |
i.e. como A1>A2, será F12<F21 (y en esa relación de áreas).
b) Para calcular F12 (factor de vista del depósito completo al parasol), se va a calcular previamente los factores de vista de cada cara (base delantera, cara lateral, y base trasera) respecto al parasol. Determinar todos estos valores numéricos.Puede aproximarse el F1l,2 (i.e. desde la superficie lateral de 1, al 2) por el factor de vista bidimensional de la sección recta.
De la base delantera (1d) al parasol (2), encontramos F1d2 en la Tabla (Unequal discs). Es de esperar que sea casi F1d2=1.
| > | eqF1d2:=F1d2=(x-y)/2;y:=sqrt(x^2-4*(r2/r1)^2);x:=1+(1+r2^2)/r1^2;r1:=D1/(2*Ls);r2:=D2/(2*Ls);r1_r2_x_y_:=subs(dat,[r1,r2,x,y]);F1d2_:=subs(dat,rhs(eqF1d2)); |
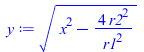 |
i.e. F1d2=0,99, que significa que el 99 % de lo que emite la base delantera incide en el parasol.
El F1l2 (desde la superficie lateral de 1, al 2) puede calcularse de varias maneras:
b1). Aproximándolo por el factor de vista bidimensional de la sección recta.
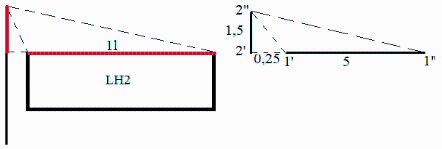
| > | eqL2:=L2=(D2-D1)/2;eqL2_:=subs(dat,%);eqF1l2:=F1l2=(L1p2s+L2s1p-L1p2p-L2s2s)/(2*L1p1s);eqF1l2:=F1l2=(sqrt(L2^2+Ls^2)+(Ls+L1)-Ls-sqrt((Ls+L1)^2+L2^2))/(2*L1);eqF1l2_:=subs(eqL2,dat,SI0,%);F1l2did_:=%: |
i.e. con el modelo 2D, F1l2=0,11.
b2). Con la expresión para Outer surface of cylinder to annular disc joining the base. Si despreciamos la separación Ls=0,25 m frente a las otras dimensiones (la más pequeña es D1=1,5 m), i.e. si consideramos que el parasol es coplanario con la base:
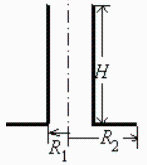
| > | x:='x':y:='y':r:='r':h:='h':eqF1l2:=F1l2=y/(8*r*h)+1/(2*Pi)*(arccos(x/y)-z*arccos(x*r/y)/(2*h)-(x*arcsin(r)/(2*r*h)));x:=h^2+r^2-1;y:=h^2-r^2+1;z:=sqrt(((x+2)/r)^2-4);eqr:=r=D1/D2;eqr_:=subs(dat,%);eqh:=h=2*L1/D2;eqh_:=subs(dat,%);r_h_x_y_z:=subs(eqr_,eqh_,[r,h,x,y,z]);F1l2_:=evalf(subs(eqr_,eqh_,rhs(eqF1l2))); |
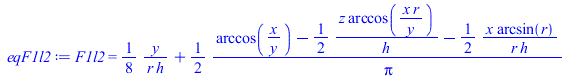 |
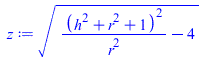 |
i.e. con el modelo 3D, F1l2=0,10 (solo un 6 % menor que el 2D).
Si no despreciamos la separación Ls, tomaríamos dos cilindros de diámetro D1=1,5 m y bases coplanarias con el parasol, uno de altura Ls (nodo 1s), y otro de altura Ls+L1 (nodo 1c, combinado), como se muestra en la figura, aplicaríamos la ecuación anterior, y luego haríamos la composición (con A1c=A1l+A1s):
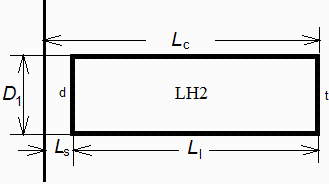
| > | eqFs_cil:=A1c*F1c2=A1s*F1s2+A1l*F1l2;A1c_:=evalf(subs(dat,Pi*D1*(Ls+L1)));F1c2_:=evalf(subs(r=D1/D2,h=2*(Ls+L1)/D2,dat,rhs(eqF1l2)));A1s_:=evalf(subs(dat,Pi*D1*Ls));F1s2_:=evalf(subs(r=D1/D2,h=2*Ls/D2,dat,rhs(eqF1l2)));A1l_:=evalf(subs(dat,Pi*D1*L1));F1l2_:=subs(dat,(Pi*D1*(Ls+L1)*F1c2_-Pi*D1*Ls*F1s2_)/(Pi*D1*L1)); |
i.e. el verdadero valor de F1l2 (lateral del tanque al parasol) es F1l2=0,077 (un 7,7 % de lo que emitiera iría a 2) en vez del valor aproximado antes calculado F1l2=0,100, o el 2D F1l2=0,106. Nótese la importancia de la separación L0=0,25 m, despreciable frente a los L1=5 m del depósito y sin embargo importante para los factores de vista y por tanto para los efectos térmicos.
Para el tanque en su conjunto (bases más lateral), el F12 se determina por composición de los factores anteriores:
| > | eqFtank:=F12=(A1d*F1d2+A1l*F1l2+A1t*0)/(A1d+A1l+A1t);eqFtank_:=subs(F1l2=F1l2_,F1d2=F1d2_,A1t=A1d,eqA1d_,eqA1l_,dat,%);eqFpara:=F21=A1*F12/A2;eqFpara_:=subs(eqFtank_,eqA1_,eqA2_,eqFpara);eqFtank2_:=subs(F1l2did_,F1d2=F1d2_,A1t=A1d,eqA1d_,eqA1l_,eqFtank);eqFpara2_:=subs(eqFtank2_,eqA1_,eqA2_,eqFpara); |
i.e. para el tanque en su conjunto F12=0,13 con el modelo 3D (F12=0,16 con el 2D). Nótese que las contribuciones relativas en el numerador de eqFtank son parecidas: la cara delantera aporta A1d·F1d2=1,7 m2 y la lateral A1l·F1l2=1,8 m2 (que dividivo por el área del tanque, 27 m2, da el F12=(1,7+1,8)/27=0,13).
[NOTA. A partir de aquí usaremos la aproximación bidimensional antedicha. Si se quiere seguir con los valores exactos, basta hacer que eqFtank2 y eqFpara2 reflejen los valores 3D.]
c) Con el modelo de cuerpos negros, plantear el balance energético general del depósito considerando toda su superficie exterior isoterma (T1), así como la del escudo (T2). Determinar T1 para mantener el régimen estacionario.
Como se quiere mantener el LH2 sin pérdida de masa y en régimen estacionario, no puede haber flujo de calor a través de la pared del depósito, luego su temperatura exterior, Te, ha de ser igual a la interior, Ti, que es la temperatura de equilibrio líquido-vapor (ELV) del H2 a 1 MPa, 31 K según se puede calcular con la ecuación de Antoine:
| > | eq6_41;eq6_42;Ti_:=evalf(subs(dat,solve(pH=pv(T),T)));T1=subs(dat,TH);M1bb=sigma*T1^4;M1bb_:=subs(dat,sigma*TH^4); |
![p = `*`(p[u], `*`(exp(`+`(A, `-`(`/`(`*`(B), `*`(`+`(C, `/`(`*`(T), `*`(T[u]))))))))))](images/p77_58.gif) |
![T = `*`(T[u], `*`(`+`(`/`(`*`(B), `*`(`+`(A, `-`(ln(`/`(`*`(p), `*`(p[u]))))))), `-`(C))))](images/p77_59.gif) |
El balance energético del tanque es:
| > | eqBE:=m*c*dT/dt=Wdis+Qin-Qout;eqBE:=m*c*dT/dt=Wdis+Qcond+Qrad2-Qradinf;eqBEstdy:=Qcond+Qrad2=Qradinf;eqQcond:=Qcond=subs(dat,Qcond_sop);eqQrad2:=Qrad2=A1*F12*(M2bb-M1bb);eqQrad2_:=subs(eqA1_,eqFtank2_,M1bb=M1bb_,dat,%);eqQradinf:=Qradinf=A1*F1inf*(M1bb-Minf);eqQradinf_:=subs(eqA1_,F1inf=1-F12,eqFtank2_,M1bb=M1bb_,Minf=sigma*Tinf^4,dat,%); |
i.e. el tanque recibe 0,5 W por conducción en los soportes, más el intercambio radiativo con el escudo, y evacúa al vacío 1,2 W. Nótese la poca capacidad de evacuación de calor de un radiador a 31 K: lo máximo es M1bb=0,05 W/m2 (1,4 W para el tanque sin ningún escudo). Y el cambia de poner Tinf=2,7 K o Tinf=0 es irrelevante. Por eso es necesario disponer escudos fríos que tapen el sol, pues aun con alpha=0,1, el sol lateral podría suponer hasta alpha*E*D*L=1020 W.
d) Determinar T2 con el modelo anterior.
| > | eqBEstdy_:=subs(eqQcond,eqQrad2_,eqQradinf_,eqBEstdy);M2bb_:=solve(%,M2bb);T2=sqrt(sqrt(M2bb/sigma));T2_:=subs(dat,SI0,sqrt(sqrt(M2bb_/sigma)))*K_; |
i.e. con el modelo de cuerpos negros, la cara vista del escudo debe estar a T2=44 K, para que solo le añado Qrad2=0,7 W a los Qcond=0,5 W que entran en el tanque e igualen los Q1inf=1,2 W que salen al vacío de fondo. Si el escudo estubiera más caliente se iría vaporizando LH2 que habría que evacuar para mantener la presión, y si estuviera el parasol más frío se condensaría algo de H2 y disminuiría la presión y la temperatura, y con esto la emisión al vacío, hasta establecerse un nuevo estado estacionario.
e) Determinar T2 con las propiedades termo-ópticas reales dadas.
Hay que recurrir al método de las exitancias. Las incógnitas son M1, M2 y M2bb pues M1bb=sigma*T1^4. Y las ecuaciones:
| > | eqQ1rad1:=epsilon1*A1*(M1-M1bb)/(1-epsilon1)=A1*F12*(M2-M1)+A1*F1inf*(Minf-M1);eqQ1rad2:=epsilon1*A1*(M1-M1bb)/(1-epsilon1)=m1*c1*dT1/dt-Qcond;eqQ2rad1:=epsilon2*A2*(M2-M2bb)/(1-epsilon2)=A2*F21*(M1-M2)+A2*F2inf*(Minf-M2); |
que sustituyendo valores queda:
| > | eqQ1rad1_:=subs(eqA1_,M1bb=M1bb_,F1inf=1-F12,eqFtank2_,Minf=0,dat,eqQ1rad1);eqQ1rad2_:=subs(eqA1_,M1bb=M1bb_,eqQcond,dT1=0,dat,eqQ1rad2);eqQ2rad1_:=subs(eqA2_,M1bb=M1bb_,F2inf=1-F21,eqFpara2_,Minf=0,dat,eqQ2rad1);sol_:=solve({eqQ1rad1_,eqQ1rad2_,eqQ2rad1_},{M1,M2,M2bb});T2_:=subs(sol_,dat,SI0,sqrt(sqrt(M2bb/sigma)))*K_; |
i.e. con la baja emisividad del escudo, basta conseguir que esté a 161 K (en vez de a los 44 K de cuerpo negro) para mantener el tanque a 31 K.
El esquema de del circuito térmico (analogía eléctrica) es:
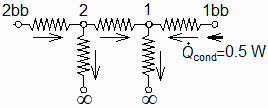
| > |
NOTA. Con el modelo de tanque isotermo estacionario, no interviene la conducción de calor a través de las paredes del depósito. Sí habría que tenerla en cuenta para los transitorios, y para el estudio de depósito no isotermo, que será imprtante ya que la entrada de calor es solo por la izquierda (por el lado del parasol), por lo que el gradiente de temperatura axial en la superficie será grande.
En este caso, T1(x), habría que resolver el problema discretizando la superficie cilíndrica en varios tramos, o resolviendo el problema diferencial. También pudiera ser que el parasol no fuese isotermo y hubiera que considerar una variación radial T2(r). Para estos casos, los factores de vista entre elementos diferenciales podrían obtenerse por derivación de la expresión analítica del F12 entre superficies finitas.
Si se tratara de tener almacenados LH2 y LOX, habría que aislar el tanque de LH2 del de LOX, que estará a >100 K (la temperatura de ebullición del O2 es Tb=90 K).
Este ejercicio está inspirado en Plachta-2006. de donde se ha tomado la figura siguiente. Nótese que si se trata de tener almacenados LH2 y LOX, habría que aislar el tanque de LH2 del de LOX, que estará a >100 K (la temperatura de ebullición del O2 es Tb=90 K, y la del H2 Tb=20 K).
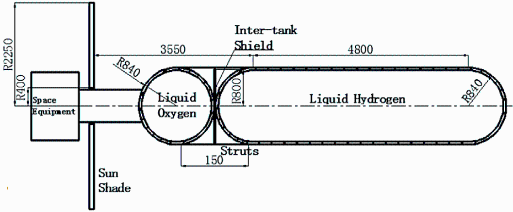
| > |
ADICIONAL
f) Calcular la carga térmica máxima terrestre que recibiría el depósito si estuviese en órbita geoestacionaria.
Lo más importante será la emisión infrarroja a 90º respecto al Sol (i.e. cuando desde la Tierra se ve transversalmente el cilindro. El albedo aquí es pequeño porque se ve solo media Tierra iluminada (y cuando el albedo sería más intenso, justo en la posición subsolar, solo le daría a la cara trasera del depósito, y el recubrimiento es reflectante solar.
Si aproximamos el cilindro por una placa plana con su misma sección transversal, Ap=D1*L, el factor de vista sería F12=1/h^2=(RE/RGEO)^2=0,023 y el calor absorbido en el IR:
| > | datGEO:=RE=6371e3*m_,RGEO=42164e3*m_,epsilonE=0.6,TE=288*K_;QdotIR:=epsilon1*A[p]*F[pE]*epsilon[E]*sigma*T[E]^4;eqAp:=A[p]=D1*L1;evalf(subs(dat,%));F12plano:=1/h^2;F12plano:=(R[E]/R[GEO])^2;F12plano_:=evalf(subs(datGEO,dat,(RE/RGEO)^2));QdotIR_:=subs(eqAp,datGEO,dat,epsilon1*A[p]*F12plano_*epsilonE*sigma*TE^4); |
![`/`(`*`(`^`(R[E], 2)), `*`(`^`(R[GEO], 2)))](images/p77_91.gif) |
i.e. 36 W, una enormidad comparado con los valores anteriores (del orden de 1 W). Si se hiciese más exactamente con la forma cilíndrica en lugar de la proyección frontal, el resultado sería casi igual, pues aunque el factor de vista para todo el cilindro sería solo F12=0,007, ahora el área involucrada es mayor:
| > | x:='x':eqAp:=A[p]=Pi*D1*L1;evalf(subs(dat,%));F12cil_lat:=(4/Pi^2)*Int(x*EllipticE(x)/sqrt(1-x^2),x=0..1/h);F12cil_lat_:=evalf(subs(h=RGEO/RE,datGEO,value(%)));QdotIR_:=subs(eqAp,datGEO,dat,epsilon1*A[p]*F12cil_lat_*epsilonE*sigma*TE^4);; |
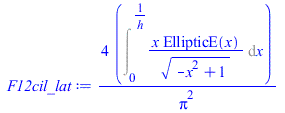 |
Con este aporte de calor, para mantener la presión habría que estar evacuando mdot_vap:=Qdot/hlv=36/255=0,14 g/s (12 t/d), siendo hlv=255 kJ/kg a 31 K (a 20 K es hlv=448 kJ/kg).
Nótese lo poco eficiente que es la radiación a temperaturas criogénicas; para evacuar 1 W en un entorno a Tinf=2.7 K, un radiador ideal necesitaría un área:
| > | A1:=Q1/(sigma*(T^4-Tinf^4));A1_:=subs(Q1=1,T=T_K,dat,SI0,%);plot(A1_,T_K=0..50,A_m2=0..500); |
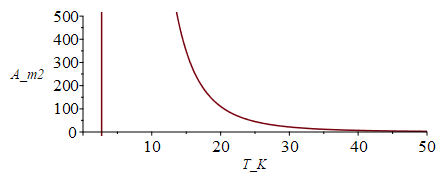 |
i.e. se necesitarían 1 m2 a 65 K, pero 110 m2 a 20 K.
Conclusión, es dificilísimo mantener depósitos de LH2 sin pérdidas de forma pasiva; lo más sensato sería incorporar refrigeradores criogénicos movidos por energía solar.
| > |