Considérese una caja cúbica hueca de 0,2 m de arista y 5 mm de espesor, en órbita geoestacionaria con el sol perpendicular a una de sus aristas simétricamente, pudiéndose despreciar el efecto de otros cuerpos. Para un primer análisis térmico, se va a suponer que todas las paredes son cuerpos negros, y que la conductividad térmica es 20 W/(m·K) en todas las direcciones. Se pide:
a) Determinar la temperatura estacionaria suponiendo que la conductividad fuese dominante. Indicar el resultado que se obtendría si la conductividad fuese despreciable.
b) Considérese un modelo de tres nodos, siendo el nodo N1 la parte iluminada (las dos caras delanteras), el nodo N2 las dos caras traseras, y el nodo N3 las dos caras laterales. Plantear las ecuaciones nodales en el régimen transitorio.
c) Determinar el factor de vista entre dos caras opuestas, F12, y a partir del valor anterior, determinar el factor de vista entre dos caras adyacentes, F13.
d) Con los valores anteriores, determinar el factor de vista entre los nodos N1 y N2, y entre los nodos N1 y N3.
e) Determinar las temperaturas de los tres nodos antedichos, en régimen estacionario, despreciando la conductividad térmica en los bordes.
f) Determinar las temperaturas de los tres nodos antedichos, en régimen estacionario, considerando la conductividad térmica en los bordes.
Datos:
| > |
read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > |
dat:=[L=0.2*m_,delta=0.005*m_,E=1361*W_/m_^2,k=20*W_/(m_*K_),Tinf=2.7*K_];dat:=op(dat),Const,SI2,SI1: |
a) Determinar la temperatura estacionaria suponiendo que la conductividad fuese dominante. Indicar el resultado que se obtendría si la conductividad fuese despreciable.
Recibe por un área frontal Afrontal=sqrt(2)*L^2, y emite por las 6 caras Atotal=6*L^2, por igual al exterior. Si es isotermo, no hay flujos de calor por el interior ni por los bordes.
Con una irradiancia solar media E=1361 W/m2,y despreciando los efectos terrestres (la GEO está muy lejos, a 6,6 radios terrestres; lo máximo sería un albedo menoe de 10 W/m2), el balance energético será:
| > |
eqBE:=m*c*dT/dt=Wdis-Qinf;eqBEstd:=0=E*Af-At*sigma*(T^4-Tinf^4);eqAf:=Af=sqrt(2)*L^2;eqAt:=At=6*L^2;T4:=E*Af/(At*sigma);T4_:=subs(eqAf,eqAt,T4);T4__:=evalf(subs(dat,%));T_:=evalf(sqrt(sqrt(subs(SI0,%))))*K_;'T_'=TKC(%);; |
i.e. todas las caras del cubo quedarían a 274 K (1 ºC).
Si la conductividad fuese despreciable. no habría flujo de calor por conducción en las esquinas, y no valdría el modelo de un solo nodo. (aunque sí habría un flujo de calor por radiación entre ellas por el interior, como se resuelve en el último apartado).
Si, además de k=0, las caras estuvieran aisladas por detrás (e.g. con MLI), las caras iluminadas recibirían radiación solar que habría de compensarse con la radiación propia hacia el espacio vacío, alcanzando una temperatura T=(E/(sqrt(2)*sigma))^(1/4)=88 ºC, mientras que las otras cuatro caras no estarían expuestas mas que a la radiación de fondo, por lo que alcanzarían Tinf=2.7 K, aunque este resultado es poco realista porque es muy difícil aislar tanto, y porque daría un poco el sol en las caras laterales (el Sol no es un foco puntual; el disco solar subtiende un semiángulo de 0,7/159=0,07 rad=4º); y también se notaría la inflencia de la Tierra (IR y albedo).
| > |
T4ais:=E*sqrt(2)/(2*sigma);Tais_:=evalf(subs(dat,SI0,%)^(1/4))*K_;'Tais_'=TKC(%); |
b) Considérese un modelo de tres nodos, siendo el nodo N1 la parte iluminada (las dos caras delanteras), el nodo N2 las dos caras traseras, y el nodo N3 las dos caras laterales. Plantear las ecuaciones nodales en el régimen transitorio.
| > |
eqN1:=m1*c1*dT1/dt=Wdis-QN1inf-QN1N2-QN1N3-k*A12*(T1-T2)/L12-k*A13*(T1-T3)/L13;eqN2:=m2*c2*dT2/dt=-QN2inf+QN1N2-QN2N3+k*A12*(T1-T2)/L12+k*A32*(T3-T2)/L32;eqN3:=m3*c3*dT3/dt=-QN3inf+QN2N3+QN1N3+k*A13*(T1-T3)/L13-k*A32*(T3-T2)/L32;Wdis:=E*Af;QN1inf:=AN1*(M1-Minf);QN2inf:=AN2*(M2-Minf);QN3inf:=AN3*(M3-Minf);QN1N2:=AN1*F[N1,N2]*(M1-M2);QN1N3:=AN1*F[N1,N3]*(M1-M3);QN2N3:=AN2*F[N2,N3]*(M2-M3);M=sigma*T^4; |
c) Determinar el factor de vista entre dos caras opuestas, F12, y a partir del valor anterior, determinar el factor de vista entre dos caras adyacentes, F13.
En la Tabla de VF, para el caso 'Equal square plates' con w=1 ya viene resuelto y es F12=0,1988, que aproxiamremos por F12=0,20.
| > |
eqF12:=F12=(ln(4/3)+4*(sqrt(2)*arctan(1/sqrt(2))-Pi/4))/Pi;eqF12_:=evalf(%);eqF1tot:=F12+4*F13=1;eqF13_:=F13=(1-rhs(eqF12_))/4; |
i.e. son prácticamente iguales (F12=0,1988 y F13=0,2003).
d) Con los valores anteriores, determinar el factor de vista entre los nodos N1 y N2, y entre los nodos N1 y N3.
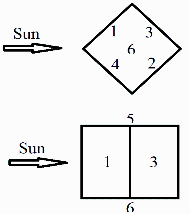
Con la nomenclatura del gráfico:
| > |
eq1:=F[N1,N2]=F["1+4","2+3"];eq1:=F[N1,N2]=(A1*F[1,"2+3"]+A4*F[4,"2+3"])/(A1+A4);eq1aux:=F[1,"2+3"]=F12+F13;eq1_:=F[N1,N2]=(L^2*(F12+F13)+L^2*(F12+F13))/(L^2+L^2);eq1__:=subs(eqF12_,eqF13_,%);eq3:=F[N1,N3]=1-F[N1,N1]-F[N1,N2];F[N1,N1]=F12;eq3_:=subs(F[N1,N1]=F12,eqF12_,eq1__,eq3);eq2:=F[N2,N3]=F[N1,N3];eq2_:=subs(eq3_,%); |
i.e. del N1 al N2 va el 40 %, de N1 a N3 va otro 40 %, y el restante 20 % va de N1 a N1.
e) Determinar las temperaturas de los tres nodos antedichos, en régimen estacionario, despreciando la conductividad térmica en los bordes.
| > |
'eqN1'=eqN1;'eqN2'=eqN2;'eqN3'=eqN3;AN=2*L^2;Minf:=0;eqN1_:=evalf(subs(eqAf,AN1=AN,AN2=AN,AN3=AN,AN=2*L^2,eq1__,eq2_,eq3_,k=0,dat,SI0,0=rhs(eqN1)));eqN2_:=evalf(subs(eqAf,AN1=AN,AN2=AN,AN3=AN,AN=2*L^2,eq1__,eq2_,eq3_,k=0,dat,SI0,0=rhs(eqN2)));eqN3_:=evalf(subs(eqAf,AN1=AN,AN2=AN,AN3=AN,AN=2*L^2,eq1__,eq2_,eq3_,k=0,dat,SI0,0=rhs(eqN3))); |
| > |
sol:=solve([eqN1_,eqN2_,eqN3_],[M1,M2,M3]);T1_:=evalf(subs(op(sol),dat,SI0,(M1/sigma)^(1/4)))*K_;'T1'=TKC(%);T2_:=evalf(subs(op(sol),dat,SI0,(M2/sigma)^(1/4)))*K_;'T2'=TKC(%);T3_:=evalf(subs(op(sol),dat,SI0,(M3/sigma)^(1/4)))*K_;'T3'=TKC(%); |
i.e. las caras frontales quedan a 49 ºC, y todas las demás (las otras cuatro) a -37 ºC. Parece curioso que queden a igual T las caras laterales y las traseras, pero es por haber despreciado la conductividad (y ser casi iguales los factores de vista).
f) Determinar las temperaturas de los tres nodos antedichos, en régimen estacionario, considerando la conductividad térmica en los bordes.
Con k=20 W/(m·K).
| > |
eqN1_:=0=rhs(eqN1);eqN2_:=0=rhs(eqN2);eqN3_:=0=rhs(eqN3);A12:=2*L*delta;A13:=4*L*delta;A32:=A13;L12:=2*L;L13:=L/2+sqrt(2)*L/2;L32:=L13;eqN1__:=evalf(subs(M1=sigma*T1^4,M2=sigma*T2^4,M3=sigma*T3^4,eqAf,AN1=AN,AN2=AN,AN3=AN,AN=2*L^2,eq1__,eq2_,eq3_,dat,SI0,0=rhs(eqN1_)));eqN2__:=evalf(subs(M1=sigma*T1^4,M2=sigma*T2^4,M3=sigma*T3^4,eqAf,AN1=AN,AN2=AN,AN3=AN,AN=2*L^2,eq1__,eq2_,eq3_,dat,SI0,0=rhs(eqN2_)));eqN3__:=evalf(subs(M1=sigma*T1^4,M2=sigma*T2^4,M3=sigma*T3^4,eqAf,AN1=AN,AN2=AN,AN3=AN,AN=2*L^2,eq1__,eq2_,eq3_,dat,SI0,0=rhs(eqN3_)));sol:=fsolve({eqN1__,eqN2__,eqN3__},{T1,T2,T3},T1=100..500);T1_:=subs(sol,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol,T2)*K_;'T2_'=TKC(%);T3_:=subs(sol,T3)*K_;'T3_'=TKC(%); |
i.e. las caras frontales quedan a 32 ºC (en vez de a 49 ºC), las laterales a -16 ºC y las traseras a -23 ºC (antes ambos conjuntos quedaban a -37 ºC. Si la conductividad fuese 200 W/(m·K) el resultado sería más próximo al caso isotermo inicial de 274 K: T1=282 K, T2=269 K, y T3=272 K.

![Typesetting:-mprintslash([eqF12 := F12 = `/`(`*`(`+`(ln(`/`(4, 3)), `*`(4, `*`(`^`(2, `/`(1, 2)), `*`(arctan(`+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(1, 2))))))))), `-`(Pi))), `*`(Pi))], [F12 = `/`(`*`(`+`(l...](images/p75_26.gif)