p731.html

> restart:#"m13_p73"

Considérese un objeto esférico negro de 0,1 m de diámetro a 250 km de altitud formando ángulo recto con el Sol y el centro de la Tierra, en enero. Se pide:
a. Balance energético no estacionario.
b. Carga térmica solar.
c. Cargas térmicas planetarias.
d. Temperatura que alcanzaría si estuviese en estado estacionario en ese punto.
e. Indicar qué datos adicionales hacen falta para calcular la evolución de la temperatura a lo largo de una órbita perpendicular, y de otra órbita que contenga la dirección Sol-Tierra
Datos:

> read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):unprotect(phi):

> dat:=[D=0.1*m_,H=250e3*m_,E=1361*W_/m_^2,Tinf=2.7*K_,rho[p]=0.3,epsilon[p]=0.61,Tp=288*K_,alpha[s]=1,epsilon[s]=1];dat:=op(dat),Const,SI2,SI1:

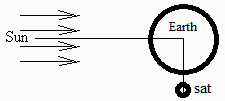
a) Balance energético no estacionario.

Para simplificar se considera solo un nodo (esfera isoterma) y cuerpo negro ideal. Además, por estar sobre el terminador, el albedo es despreciable.

> eqBE:=m*c*dT/dt=Wdis+Qin-Qout;eqBE:=m*c*dT/dt=Wdis+Qs+Qa+Qp-Qinf;eqBE:=m*c*dT/dt=Qs+Qp-Qinf;

b) Carga térmica solar.

Es lo que absorbe directamente del Sol. Si es cuerpo negro alpha=1.

> Qs:=alpha[s]*Af*E*Fs;eqAs:=As=Pi*D^2;eqAf:=Af=Pi*D^2/4;Qs_:=subs(Fs=1,eqAf,dat,Qs);

i.e. la carga solar es de 10,7 W.

Cargas térmicas planetarias.

Ya se ha dicho que el albedo es despreciable (suele modelizarse con el coseno del ángulo). La planetaria de IR es:

> Qp:=epsilon[s]*As*Fsp*epsilon[p]*sigma*Tp^4;

Tomaremos la absortancia del satélite (igual a la emisividad del satélite) e[s]=1 por ser cuerpo negro, y la del planeta e[p]=0,61, pero falta calcular el factor de vista desde la esfera pequeña a la grande. Mirando en la Tabla:

> eqFsp:=Fsp=(1/2)*(1-sqrt(1-1/(1+h)^2));eqh:=h=H/R[T];eqh_:=subs(dat,%);eqFsp_:=subs(eqh_,eqFsp);Qp_:=subs(eqAs,eqFsp_,dat,Qp);

i.e. el 35 % de lo que emite el satélite (esfera pequeña) va al planeta (y el otro 65 % al fondo del universo), y la carga IR proveniente del planeta (no la neta) es de 2,7 W.

d) Temperatura que alcanzaría si estuviese en estado estacionario en ese punto.

> eqBEst:=0='Qs+Qp-Qinf';Qinf:=epsilon[s]*sigma*As*(T^4-Tinf^4);eqBEst_:=subs(eqAs,eqAf,Fs=1,eqFsp_,dat,SI0,eqBEst);T0_:=max(fsolve(%,T))*K_;'T0_'=TKC(%);

i.e. para evacuar la absorción total (Qs+Qp=13,4 W) el satélite debe estar a 295 K (21 ºC).

e) Indicar qué datos adicionales hacen falta para calcular la evolución de la temperatura a lo largo de una órbita perpendicular, y de otra órbita que contenga la dirección Sol-Tierra.

Si el ángulo solar de la órbita es beta=90º (órbita de amanecer-anochecer), sería T=cte en toda la órbita. Si fuera beta=0, haría falta saber la inercia térmica (mc) para integrar la eqBE.