| > | restart:#"m13_p72" |
Considérese un satélite esférico de 2,3 m de diámetro en una órbita terrestre de 300 km de altitud coplanaria con la dirección Sol-Tierra. Suponiendo que hay una generación térmica interna de 1 kW, que la temperatura del satélite pueda considerarse uniforme, y que sus propiedades termo-ópticas son =0,9 y =0,9, se pide:
a) Plantear el balance energético transitorio en un punto genérico de la órbita.
b) Carga térmica solar y temperatura estacionaria con sol pero sin efectos terrestres.
c) Factor de vista con la Tierra.
d) Carga por emisión planetaria.
e) Carga por albedo, y representación gráfica de su evolución (y de las demás cargas).
f) Temperatura estacionaria en el punto subsolar y en el opuesto.
g) Temperatura media correspondiente al valor medio orbital de las cargas térmicas.
h) Temperatura estacionaria (i.e. sin inercia térmica) en cada punto de la órbita.
i) Evolución de la temperatura a lo largo de la órbita (con inercia térmica).
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):unprotect(phi): |
| > | dat:=[D=2.3*m_,m=2400*kg_,c=500*J_/(kg_*K_),alpha[s]=0.9,epsilon[s]=0.9,E=1361*W_/m_^2,Tinf=2.7*K_,Wdis=1e3*W_,H=300e3*m_,rho[p]=0.3,epsilon[p]=0.61,Tp=288*K_];dat:=op(dat),Const,SI2,SI1: |
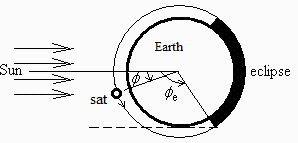
a) Plantear el balance energético transitorio en un punto genérico de la órbita.
| > | eqBE:=m*c*dT/dt=Wdis+Qin-Qout;eqBE:=m*c*dT/dt=Wdis+Qs+Qa+Qp-Qinf; |
i.e. su temperatura aumentará con la disipación interna (Wdis, e.g. proveniente de acumuladores eléctricos, metabolismo...), con la absorción solar directa (Qs), con el albedo (solar reflejada, Qs), y con la emisión planetaria, y se enfria con la emisión en todas direcciones (ya que del planeta solo contabilizamos su emisión y no el intercambio radiativo).
b) Carga térmica solar y temperatura estacionaria con sol pero sin efectos terrestres.
| > | Qs:=alpha[s]*Af*E*Fs;Qinf:=epsilon[s]*sigma*As*(T^4-Tinf^4);eqAs:=As=Pi*D^2;eqAf:=Af=Pi*D^2/4;Qs_:=subs(Fs=1,eqAf,dat,Qs);eqBEs:=0=subs(Fs=1,Tinf=0,Wdis+Qs-Qinf);eqBEs_:=subs(eqAs,eqAf,dat,SI0,%);T0_:=max(fsolve(%,T))*K_;'T0_'=TKC(%); |
i.e. el satélite quedaría a 18 ºC teniendo en cuenta la disipación interna; una esfera expuesta solo al sol y a la radiación de fondo, a 1 ua, quedaría a 5 ºC, independientemente del tamaño; en nuestro caso la esfera absorbe 5,1 kW del sol, y emite al espacio 6,1 kW. El factor Fs introducido en la carga solar es Fs=1 si hay sol y Fs=0 si no le da el sol (eclipse).
c) Factor de vista con la Tierra.
Mirando en la Tabla, para una esfera pequeña con una esfera grande:
| > | eqFsp:=Fsp=(1/2)*(1-sqrt(1-1/(1+h)^2));eqh:=h=H/R[T];eqh_:=subs(dat,%);eqFsp_:=subs(eqh_,eqFsp); |
i.e. el 35 % de lo que emite el satélite (esfera pequeña) va al planeta, y el otro 65 % al fondo del universo. Si ampliáramos el radia terrestre para incluir la atmósfera efeciva (poniendo RT=6400 km en vez de RT=6370 km) el resultado sería casi igual.
d) Carga por emisión planetaria.
| > | Qp:=epsilon[s]*As*Fsp*M[OLR];Qp:=epsilon[s]*As*Fsp*epsilon[p]*sigma*Tp^4;Qp_:=subs(eqAs,eqFsp_,dat,%);M[OLR]=subs(dat,epsilon[p]*sigma*Tp^4); |
i.e. la Tierra emite 238 W/m2 (OLR=outgoing longwave radiation) y el satélite absorbe 1,3 kW (en el infrarrojo). Esta carga es constante en toda la órbita (Tierra isoterma).
e) Carga por albedo, y representación gráfica de su evolución (y de las demás cargas).
| > | Qa:=Qam*Fa;Qa:=alpha[s]*As*Fsp*rho[p]*E*Fa;Qam_:=subs(eqAs,eqFsp_,dat,Qa/Fa); |
i.e. la carga máxima por albedo es de 2,1 kW (en el punto subsolar). Para el factor temporal de albedo tomaremos el modelo simple del coseno, mientras que para el factor solar hay que calcular los ángulos de eclipse. Para graficar la evolución de las cargas conviene construir funciones continuas a trozos:
| > | Fa:=piecewise(arccos(cos(phi))<Pi/2,1,arccos(cos(phi))>2*Pi-Pi/2,1,0)*cos(phi);plot(Fa,phi=0..2*Pi,'Fa'=0..1);Fs:=piecewise(arccos(cos(phi))<ee,1,arccos(cos(phi))>2*Pi-ee,1,0);ee:=Pi/2+arccos(R[T]/(R[T]+H));ee:=evalf(subs(dat,%));'ee'=evalf(%*180/Pi)*'º';plot(Fs,phi=0..2*Pi);plot(subs(dat,SI0,[Wdis,Qs_*Fs,Qam_*Fa,Qp_]),phi=0..2*Pi,Q_W=0..6000); |
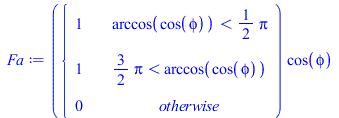 |
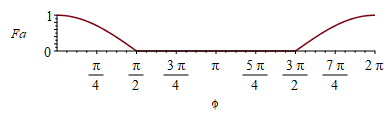 |
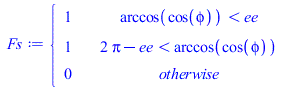 |
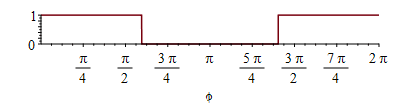 |
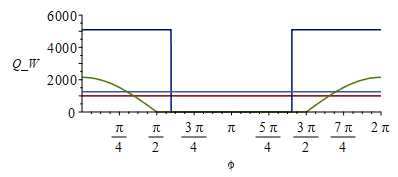 |
i.e. aunque el albedo decae con el coseno hasta 90º, el satélite no entra en eclipse hasta los 107º.
f) Temperatura estacionaria en el punto subsolar y en el opuesto.
Para phi=0 (punto subsolar):
| > | eqBE0:=evalf(subs(m=0,phi=0,eqAf,eqAs,eqFsp_,dat,SI0,eqBE));T_0_:=max(fsolve(%,T))*K_;'T_0_'=TKC(%); |
y para phi=180º:
| > | eqBE180:=evalf(subs(m=0,phi=Pi,eqAf,eqAs,eqFsp_,dat,SI0,eqBE));T_180_:=max(fsolve(%,T))*K_;'T_10_'=TKC(%); |
i.e. si estuviera permanentemente en el punto subsolar el satélite alcanzaría 52 ºC, y en eclipse -46 ºC.
g) Temperatura media correspondiente al valor medio orbital de las cargas térmicas.
Si la aproximamos por la que se alcanzaría promediando las cargas térmicas:
| > | eqBE:=m*c*dT/dt=Wdis+Qin_mean-'Qinf';Qin_mean:=Qs_mean+Qa_mean;Qs_mean:=alpha[s]*Af*E*Fs_mean;Fs_mean:=Int('Fs',phi=0..2*Pi)/(2*Pi);Fs_mean:=value(%);Facos_mean:=Int('Fa',phi=0..2*Pi)/(2*Pi);Facos_mean:=evalf(value(%));eqBE:=m*c*dT/dt=Wdis+alpha[s]*Af*E*'Fs_mean'+eval(subs(phi=0,Qa))*'Facos_mean'+Qp-Qinf;eqBE_:=subs(dT=0,eqAs,eqAf,eqFsp_,dat,SI0,%);T0_:=fsolve(%,T=200..500)*K_;T0:=((Wdis+alpha[s]*Af*E*'Fs_mean'+alpha[s]*As*Fsp*rho[p]*E*'Facos_mean'+Qp)/(epsilon[s]*As*sigma))^(1/4);T0_:=evalf(subs(eqAs,eqAf,eqFsp_,dat,SI0,%))*K_;'T0_'=TKC(%);; |
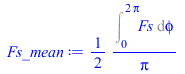 |
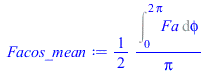 |
![`*`(`^`(`/`(`*`(`+`(`*`(As, `*`(Fsp, `*`(`^`(Tp, 4), `*`(sigma, `*`(epsilon[p], `*`(epsilon[s])))))), `*`(As, `*`(E, `*`(Fsp, `*`(Facos_mean, `*`(alpha[s], `*`(rho[p])))))), `*`(Af, `*`(E, `*`(Fs_mean...](images/p72_50.gif) |
i.e. la temperatura media orbital sería de 290 K (16 ºC).
h) Temperatura estacionaria (i.e. sin inercia térmica) en cada punto de la órbita.
| > | eqBE:=m*c*dT/dt=Wdis+'Qs+Qa+Qp-Qinf';eqBE:=subs(dT=0,eqBE);T_:=(solve(subs(T^4=T4,%),T4))^(1/4);plot(subs(eqAs,eqAf,eqFsp_,dat,SI0,T_-273),phi=0..2*Pi,T_C=-50..100); |
![0 = `+`(Wdis, `*`(alpha[s], `*`(Af, `*`(E, `*`(piecewise(`<`(arccos(cos(phi)), 1.871857043), 1, `<`(4.411328265, arccos(cos(phi))), 1, 0))))), `*`(alpha[s], `*`(As, `*`(Fsp, `*`(rho[p], `*`(E, `*`(pie...](images/p72_54.gif) |
![`*`(`^`(`/`(`*`(`+`(`*`(epsilon[s], `*`(As, `*`(Fsp, `*`(epsilon[p], `*`(sigma, `*`(`^`(Tp, 4))))))), `*`(alpha[s], `*`(As, `*`(Fsp, `*`(rho[p], `*`(E, `*`(piecewise(`<`(arccos(cos(phi)), 1.570796327)...](images/p72_57.gif) ![`*`(`^`(`/`(`*`(`+`(`*`(epsilon[s], `*`(As, `*`(Fsp, `*`(epsilon[p], `*`(sigma, `*`(`^`(Tp, 4))))))), `*`(alpha[s], `*`(As, `*`(Fsp, `*`(rho[p], `*`(E, `*`(piecewise(`<`(arccos(cos(phi)), 1.570796327)...](images/p72_58.gif) |
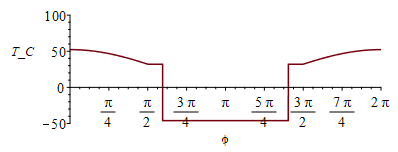 |
i.e. se ve cómo iría bajando del máximo (51 ºC) al mínimo (-49 ºC).
i) Evolución de la temperatura a lo largo de la órbita (con inercia térmica).
Usaremos posición angular en vez de tiempos, con phi=2·Pi·t/To, siendo To el periodo orbital
| > | eqBE:=m*c*dT/dt=Wdis+'Qs+Qa+Qp-Qinf';eqBE_:=m*c*Diff(T,phi)*2*Pi/To=rhs(eqBE);eqTo:=To=2*Pi*sqrt(a^3/(G*M));To_:=subs(a=R[T]+H,G=6.67e-11,M=6e24,dat,SI0,rhs(%))*s_;eqBE__:=evalf(subs(To=To_,eqAs,eqAf,eqFsp_,dat,SI0,eqBE_));eqBE___:=subs(phi=x,T=T(x),eqBE__);sol_:=dsolve([eqBE___,T(0)=300],T(x),numeric);N:=599:Norb:=9;plot([seq([rhs(op(1,sol_(Norb*2*Pi*i/N))),rhs(op(2,sol_(Norb*2*Pi*i/N)))],i=0..N)],phi=0..2*Pi*Norb,T_K=280..310);plot([seq([(rhs(op(1,sol_(Norb*2*Pi*i/N)))-2*Pi*(Norb-1)),rhs(op(2,sol_(Norb*2*Pi*i/N)))-273.15],i=N-N/Norb..N)],phi_rad=0..2*Pi,T_C=10..20);Tmin=min([seq([rhs(op(2,sol_(Norb*2*Pi*i/N)))-273.15],i=N-N/Norb..N)])*`ºC`;Tmax=max([seq([rhs(op(2,sol_(Norb*2*Pi*i/N)))-273.15],i=N-N/Norb..N)])*`ºC`; |
![`+`(`/`(`*`(2, `*`(m, `*`(c, `*`(Diff(T, phi), `*`(Pi))))), `*`(To))) = `+`(Wdis, `*`(alpha[s], `*`(Af, `*`(E, `*`(piecewise(`<`(arccos(cos(phi)), 1.871857043), 1, `<`(4.411328265, arccos(cos(phi))), ...](images/p72_61.gif) |
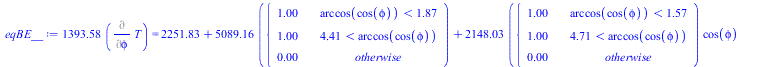 |
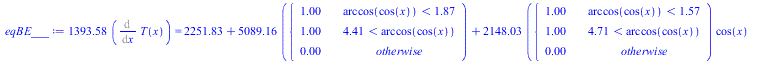 |
 |
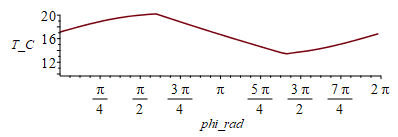 |
i.e. las condiciones iniciales (arbitrarias) tardan en amortiguarse por la gran inercia térmica del satélite, alcanzándose el régimen periódico con una Tmax=20 ºC y una Tmin=13 ºC.
NOTA. Este cápsula esférica tiene las mismas dimensiones que la cápsula de reentrada (Vostok-1, en 1961) del primer astronauta (Yuri Gagarin). Sin embargo, durante la órbita (que no fue circular) esta cápsula iba unida al módulo de servicio cuyo cohete la hizo reentrar.
| > |