| > | restart:#"m13_p71.mw" |
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots): |
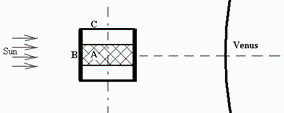
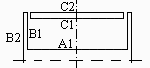
Para el estudio térmico preliminar de un pequeño satélite en órbita alrededor de Venus a 500 km de altitud y en el plano ecuatorial, se propone el siguiente modelo. Se trata de un satélite cilíndrico estabilizado por rotación, de 70 cm de diámetro y 70 cm de altura. En su interior hay una plataformas porta-instrumentos (zona A en la Fig. 1) que se aproximan a un cilindro plano de 30 cm de altura, 50 kg de masa y 1000 J/(kg·K) de capacidad térmica, con 100 W de disipación eléctrica continua. La envoltura cilíndrica exterior (zona B en la Fig. 1), tiene un grosor de 1 cm, 5 kg de masa, la misma capacidad térmica específica, una conductividad efectiva de 5 W/m·K), y está completamente cubierta con células solares. Dos placas base idénticas (C en la Fig. 1) cierran el cilindro en ambos extremos; Las propiedades de estos paneles deben seleccionarse para resolver los requisitos térmicos de la zona del instrumento dentro del rango operativo de 0 ºC a 50 ºC. Para comenzar con el análisis, los paneles C se pueden modelizar como estructuras de nido de abeja de 5 mm de espesor, hechas de hoja de aluminio de 0.1 mm de espesor, en celdas hexagonales con 5 mm de lado a lado, cubiertas por láminas delgadas pintadas de negro. Todas las caras internas pueden suponerse cuerpos negros, y el conjunto A+B puede considerarse isotérmico. Se pide:
a) Determinar las cargas térmicas (solar, de albedo e infrarroja) en función de la posición orbital.
b) Determinar la conductancia térmica entre cada nodo.
c) Determinar los factores de vista y los acoplamientos radiativos entre cada nodo.
d) Establecer las ecuaciones nodales.
e) Determinar las temperaturas que se alcanzarían con la nave en el punto subsolar, supuesto régimen estacionario.
f) Lo mismo, pero en el punto opuesto de la órbita.
g) Determinar la duración del periodo de eclipse y compararlo con el tiempo de relajación térmica de la nave.
h) Determinar la evolución de las temperaturas a lo largo de la órbita en el estado periódico.
i) Rediseñar los paneles C si fuera necesario.

Data:
| > | dat:=[H=500e3*m_,D=0.7*m_,L=0.7*m_,delta[A]=0.3*m_,mA=50*kg_,cA=1000*J_/(kg_*K_),Wdis=100*W_,delta[B]=0.01*m_,mB=5*kg_,cB=1000*J_/(kg_*K_),kB=5*W_/(m_*K_),alpha[B]=0.75,epsilon[B]=0.75,delta[C]=5e-3*m_,delta[alu]=0.1e-3*m_,s[alu]=5e-3*m_];datV:=[R=6.05e6*m_,M=4.87e24*kg_,Rsv=0.72*AU,E=1361*(W_/m_^2)/0.72^2,epsilon[p]=0.013,rho[p]=0.76,T[p]=737*K_];datAlu:=[rho[alu]=2700*kg_/m_^3,c[alu]=900*J_/(kg_*K_),k[alu]=140*W_/(m_*K_)];dat:=op(dat),op(datV),op(datAlu),Const,SI2,SI1: |
a) Determinar las cargas térmicas (solar, de albedo e infrarroja) en función de la posición orbital.
Solo hay dos nodos: el AB (suma de A y B) y el C (cada una de las bases). Las propiedades teroópticas las tomamos de la Tabla. Con Sol puntual no se iluminan las bases C.
Solar. Sean phie y phis los ángulos orbitales de entrada y salida del eclipse.
| > | QsC:=0;QsB:=alpha[B]*E*AfB;AfB:=D*L;AfB_:=subs(dat,%);QsB_:=subs(dat,QsB);phie=Pi/2+arccos(1/(1+h));h=H/R;h_:=subs(dat,H/R);phie_:=evalf(subs(h=h_,Pi/2+arccos(1/(1+h))));%*180*`º`/Pi;phis_:=evalf(2*Pi-phie_);%*180*`º`/Pi;QsB__:=piecewise(phi<phie_,QsB_,phi>phis_,QsB_,0);plot(subs(SI0,%),phi=0..2*Pi,Q_W=0..1000);pl_sB:=%:QBmean:=int(QsB__,phi=0..2*Pi)/(2*Pi); |
 |
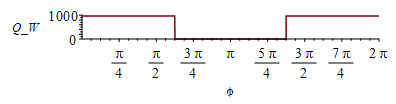 |
i.e. la nave absorbe del Sol directo 965 W y nada en eclipse, con una media de 603 W. Nótese que si la disipación eléctrica es de 100 W, quiere decirse que se han generado al menos 100 W eléctricos de media en las células solares (una pequeña parte no se habrá disipado térmicamente, sino que se habrá emitido como microondas para las telecomunicaciones). Como en eclipse no funcionan las células solares, con sol producen 100·(965/603)=160 W, o 160/0.49=327 W/m2 de superficie frontal, por lo que su rendimiento eléctrico será al menos de eta=327/2625=0,12, bastante bajo para aplicaciones espaciales, donde eta>0.20; y aún sería menor eta si se contabiliza el albedo.
Albedo. El factor de vista de C al planeta se obtiene de la Tabla (Patch to sphere), y el de B al planeta se obtiene de la Tabla (Cylinder to large sphere).
| > | Qa:=alpha*As*Fsp*rho[p]*E;QaC:=Ac*Fcp*rho[p]*E;Ac=Pi*D^2/4;Ac_:=evalf(subs(dat,Pi*D^2/4));Fcp:=(1/Pi)*(arctan(1/x)-x/(1+h)^2);x:=sqrt(h^2+2*h);Fcp_:=evalf(subs(h=h_,Fcp));QaC_:=subs(dat,Ac_*Fcp_*rho[p]*E);QaC__:=piecewise(phi<Pi/2,%*cos(phi),phi>3*Pi/2,%*cos(phi),0):x:='x':QaB:=alpha[B]*Ab*Fbp*rho[p]*E;Ab=Pi*D*L;Ab_:=evalf(subs(dat,Pi*D*L));Fbp:=(4/Pi^2)*Int(x*E(x)/sqrt(1-x^2),x=0..1/(1+h));Fbp_:=(4/Pi^2)*int(x*EllipticE(x)/sqrt(1-x^2),x=0..1/(1+h_));QaB_:=subs(dat,alpha[B]*Ab_*Fbp_*rho[p]*E);QaB__:=piecewise(phi<Pi/2,%*cos(phi),phi>3*Pi/2,%*cos(phi),0):QaCBC_:=QaB_+2*QaC_;QaCBC:=piecewise(phi<Pi/2,%*cos(phi),phi>3*Pi/2,%*cos(phi),0):plot(subs(SI0,%),phi=0..2*Pi);QaCBCmean:=int(QaCBC,phi=0..2*Pi)/(2*Pi); |
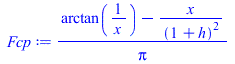 |
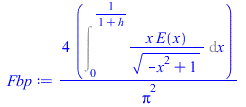 |
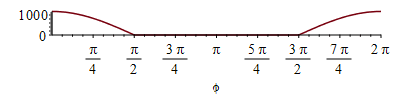 |
i.e. en el punto subsolar la nave absorbe del sol reflejado en el planeta 201 W en cada base C y1033 W en B, pero este máximo total de 1435 W apenas da 457 W de media en toda la órbita.
IR planetario.
| > | Qp:=epsilon*As*Fsp*epsilon[p]*sigma*T[p]^4;QpC:=Ac*'Fcp'*epsilon[p]*sigma*T[p]^4;QpC_:=subs(dat,Ac_*Fcp_*epsilon[p]*sigma*T[p]^4);QpB:=epsilon[B]*Ab*'Fbp'*epsilon[p]*sigma*T[p]^4;QpB_:=subs(dat,epsilon[B]*Ab_*Fbp_*epsilon[p]*sigma*T[p]^4); |
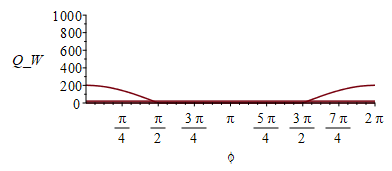
En resumen, la variación orbital de las diferentes cargas térmicas sobre una de las bases (C) y sobre la cara cilíndrica (B), son:
| > | pl_sC:=plot(0,phi=0..2*Pi,Q_W=0..1000):pl_aC:=plot(subs(SI0,QaC__),phi=0..2*Pi):pl_pC:=plot(subs(SI0,QpC_),phi=0..2*Pi):pl_aB:=plot(subs(SI0,QaB__),phi=0..2*Pi):pl_pB:=plot(subs(SI0,QpB_),phi=0..2*Pi):display([pl_sC,pl_aC,pl_pC]);display([pl_sB,pl_aB,pl_pB]); |
 |
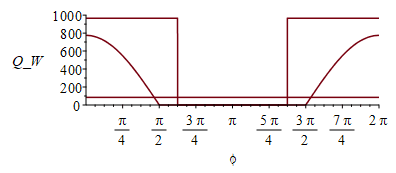 |
b) Determinar la conductancia térmica entre cada nodo.
Se trata de modelizar la transmisión de calor por conducción entre una base (disco C) y el cilindro (B). Obviamente, C y B no pueden tener temperatura uniforme y estar en contacto, porque habría un enorme flujo de calor tratando de equilibrar la unión. Lo que se quiere es estimar el flujo de calor en la forma Q=G(TB-TC) para unas temperaturas medias de TB y TC. Como se trata de en camino en serie a lo largo de dos materiales diferentes, Q=G(TB-TC)=k1A1*(TB-Ti)/L1=k2A2*(Ti-TC)/L2, siebdo Ti la temperatura en la interfac (contacto), i.e.
| > | QcondBC:=G*(TB-TC);eqQcondBC:=kB*Atb*(TB-Ti)/Lb=kC*Atc*(Ti-TC)/Lc;eqG:=G=1/(Lb/(kb*Atb)+Lc/(kc*Atc));Lb:=L/2;Lb_:=subs(dat,%);Lc:=D/4;Lc_:=subs(dat,%);Atb:=Pi*D*delta[B];Atb_:=subs(dat,%);Atc:=Pi*D*delta[C];Atc_:=subs(dat,%); |
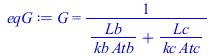 |
i.e. se ha estimado el camino a lo largo de B como, Lb=L/2=0,35 m, sin tener en cuenta el efecto de A, que lo reduciría, y para el camino a lo largo de C se ha tenido en cuenta la geometría radial y por tanto Lc=área/perímetro=Pi·R^2/(2·Pi·R)=R/2=D/4=0,175 m. Falta calcular la conductividad efectiva del panel C, con lo que se obtiene:
| > | eqkc:=kc=k[alu]*delta[alu]/s[alu];eqkc_:=subs(dat,%);eqG_:=subs(kb=kB,eqkc_,dat,eqG); |
![kc = `/`(`*`(k[alu], `*`(delta[alu])), `*`(s[alu]))](images/p71_56.gif) |
i.e. por cada 1 K de diferencia de temperatura de B a C, fluirán 0,113 W hacia la base superior y otros 0,113 W hacia la inferior.
c) Determinar los factores de vista y los acoplamientos radiativos entre cada nodo.
El factor de vista desde un disco A de diámetro DA=D-2d=0,70-2·1=0,68 m hacia otro diso C paralelo, de igual tamaño, y separados LAC=(L-deltaA-2·deltaC)/2=(0,7-0,3-2·0,01)/2=0,19 m, se obtiene de la Tabla (Equal discs).
| > | F12:=1+(1-sqrt(4*r^2+1))/(2*r^2);r:=(D-2*delta[B])/(L-delta[A]-2*delta[C]);F12_:=subs(dat,F12);Aa:=Pi*(D-2*delta[B])^2/4;Aa_:=evalf(subs(dat,%));Acylhalf:=Pi*(D-2*delta[B])*(L-delta[A]-2*delta[C])/2;Acylhalf_:=evalf(subs(dat,%)); |
![`/`(`*`(`+`(D, `-`(`*`(2, `*`(delta[B]))))), `*`(`+`(L, `-`(delta[A]), `-`(`*`(2, `*`(delta[C]))))))](images/p71_60.gif) |
i.e. el 57 % de lo que emite el disco A (de área Aa=0,36 m2) va hacia el disco C (de igual área), y el resto (43 %) va hacia la superficie cilíndrica interior vista (la mitad, de área Acylhalf=0,42 m2).
Así, el nodo C, tanto si se considera una sola base como si se consideran las dos, tiene un factor de vista del 50 % hacia el espacio profundo (lado externo), y un factor de vista del 50 % hacia el nodo A+B (57 % de este hacia A y 43 % hacia B).
En cambio, el nodo A+B tiene factores de vista más complicados por su concavidad, resultando que solo el 23 % de lo que emite va hacia el C (tanto si se considera la mitad superior/inferior del satélite como si se considera el conjunto), otro 49,7 % va hacia el espacio profundo, y el otro 27 % que sale de A+B incide sobre otras partes de A+B.
| > | F[AB,C]:='(Aa*F12+Aa*(1-F12))/(Aa+Acylhalf+Ab/2)';F[AB,C]:=(Aa_*F12_+Aa_*(1-F12_))/(Aa_+Acylhalf_+Ab_/2);F[AB,inf]:='(Ab/2)/(Aa+Acylhalf+Ab/2)';F[AB,inf]:=(Ab_/2)/(Aa_+Acylhalf_+Ab_/2);F[AB,AB]:=1-F[AB,C]-F[AB,inf] |
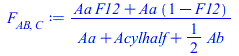 |
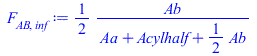 |
d) Establecer las ecuaciones nodales.
El balance energético térmico (ecuación nodal) de una de las placas de cierre, C, es:
| > | eqBE:=m*c*dT/dt=Wdis+Qcond+Qrad;eqC:=mC*cC*dTC/dt=QcondAB+QradAB+Qs+Qa+Qp-Qinf;QcondAB:=G*(TAB-TC);QradAB:=Ac*Fcab*sigma*(TAB^4-TC^4);Qs:=0;Qa:=Ac*'Fcp'*rho[p]*E*cos(phi);Qp:=Ac*'Fcp'*epsilon[p]*sigma*T[p]^4;Qinf:=Ac*sigma*TC^4; |
donde se ha hecho uso de la reciprocidad AabFab,c=AcFc,ab y del hecho de que Fc,ab=1 (todo lo que sale de la cara C1 va a B1+A1 (ver figura), así como de que C es un cuerpo negro y el albedo que recibe es proporcional al coseno del ángulo orbital respecto al punto subsolar luego se impondrá que es nulo para 90º<phi<270º).
Sustituyendo valores:
| > | mC:=rho[alu]*(8/3)*(delta[alu]/s[alu])*Aa*delta[C];mC_:=subs(Aa=Aa_,dat,%);QcondAB_:=subs(eqG_,SI0,QcondAB);QradAB_:=subs(Ac=Aa_,Fcab=1,dat,SI0,QradAB);Qa_:=subs(dat,SI0,Ac_*Fcp_*rho[p]*E*cos(phi));Qa__:=QaC__;Qp_:=subs(dat,SI0,Ac_*Fcp_*epsilon[p]*sigma*T[p]^4);Qinf_:=subs(dat,SI0,Ac_*sigma*TC^4);eqC_:=subs(dat,SI0,mC_*c[alu]*dTC/dt=QcondAB_+QradAB_+0+Qa__+Qp_-Qinf_);Qs:='Qs':Qa:='Qa':Qp:='Qp':Qinf:='Qinf': |
![`+`(`/`(`*`(`/`(2, 3), `*`(rho[alu], `*`(delta[alu], `*`(Pi, `*`(`^`(`+`(D, `-`(`*`(2, `*`(delta[B])))), 2), `*`(delta[C])))))), `*`(s[alu])))](images/p71_80.gif) |
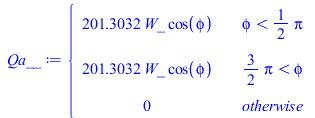 |
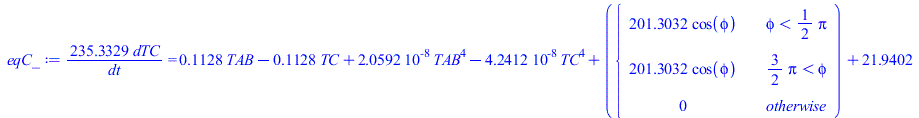 |
Para la ecuación nodal del conjunto A+B, en lugar del balance energético térmico es mejor plantear el balance energético total, con lo que no hará falta contabilizar los 100 W de electricidad disipada ni la electricidad generada en las células solares (suponiendo que sean casi iguales al despreciar la energía radiada en el enlace de telecomunicaciones). Nótese que el conjunto A+B inercambia con dos placas C.
| > | eqAB:=mAB*cAB*dTAB/dt=Qs+Qa+Qp-'2*QcondAB-2*QradAB'-Qinf;mAB:=mA+mB;mAB_:=subs(dat,%);Qs:=alpha[B]*AfB*E;Qs_:=subs(dat,%);Qs__:=QsB__;Qa:=alpha[B]*Ab*'Fbp'*rho[p]*E;Qa_:=subs(dat,SI0,alpha[B]*Ab_*Fbp_*rho[p]*E);Qa__:=QaB__;Qp:=epsilon[B]*Ab*'Fbp'*epsilon[p]*sigma*T[p]^4;Qp_:=subs(dat,SI0,epsilon[B]*Ab_*Fbp_*epsilon[p]*sigma*T[p]^4);Qinf:=epsilon[B]*Ab*sigma*TAB^4;Qinf_:=subs(Ab=Ab_,dat,SI0,%);eqAB_:=subs(eqG_,Ac=Aa_,Fcab=1,dat,SI0,mAB_*cB*dTAB/dt=Qs__+Qa__+Qp_-2*QcondAB-2*QradAB-Qinf_); |
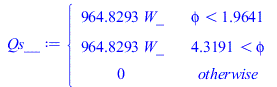 |
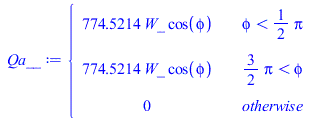 |
 |
e) Determinar las temperaturas que se alcanzarían con la nave en el punto subsolar, supuesto régimen estacionario.
Se trata de resolver las dos ecuaciones nodales en estacionario en phi=0.
| > | eqC_0:=evalf(subs(dTC=0,phi=0,eqC_));eqAB_0:=evalf(subs(dTAB=0,phi=0,eqAB_));sol_0:=fsolve({eqC_0,eqAB_0},{TC,TAB},TC=100..400);TAB=TKC(subs(sol_0,TAB*K_));TC=TKC(subs(sol_0,TC*K_)); |
i.e. si el satélite estuviese quieto sobre el punto subsolar, el cuerpo A+B alcanzaría 392 K (118 ºC) y las placas C 360 (87 ºC). Nótese que se sobrepasa el valor máximo de 50 ºC.
f) Lo mismo, pero en el punto opuesto de la órbita.
Se trata de resolver las dos ecuaciones nodales en estacionario en phi=180º.
| > | eqC_180:=evalf(subs(dTC=0,phi=Pi,eqC_));eqAB_180:=evalf(subs(dTAB=0,phi=Pi,eqAB_));sol_180:=fsolve({eqC_180,eqAB_180},{TC,TAB},TC=100..400);TAB=TKC(subs(sol_180,TAB*K_));TC=TKC(subs(sol_180,TC*K_)); |
i.e. en el eclipse estacionario se alcanzarían TAB=187 K (-86 ºC) y TC=183 K (-90 ºC). En este caso también se sobrepasa por debajo el límite frío de 0 ºC.
g) Determinar la duración del periodo de eclipse y compararlo con el tiempo de relajación térmica de la nave.
Para el tiempo de relajación supondremos enfriamiento sin aporte planetario.
| > | eqTorbit:=To=2*Pi*sqrt((R+H)^3/(G*M));To_:=subs(G=6.7e-11,dat,SI0,rhs(%))*s_;eqTeclipse:=Te=To*arcsin(1/(1+h))/Pi;eqTeclipse_:=evalf(subs(To=To_,h=h_,%));phi[e]=Pi-rcsin(1/(1+h));phie_:=evalf(subs(h=h_,Pi-arcsin(1/(1+h))));phis_:=2.*Pi-phie_;eqCooling:=m*c*dT/dt=-epsilon*A*sigma*T^4;deq:=diff(T(t),t)=-q*T(t)^4:dsolve([deq,T(0)=T0],T(t)):sol:=subs(q=epsilon*A*sigma/(m*c),%);tc:=solve((T0/2)^3=rhs(sol)^3,t);tc_:=subs(m=mAB_,c=cB,T0=390*K_,A=Ab_+2*Ac_,epsilon=epsilon[B],dat,tc);Tend_eclipse_:=subs(t=2190*s_,m=mAB_,c=cB,T0=390*K_,A=Ab_+2*Ac_,epsilon=epsilon[B],dat,rhs(sol));plot(subs(m=mAB_,c=cB,T0=390*K_,A=Ab_+2*Ac_,epsilon=epsilon[B],dat,SI0,rhs(sol)),t=0..6000,T_K=0..400); |
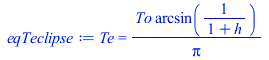 |
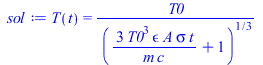 |
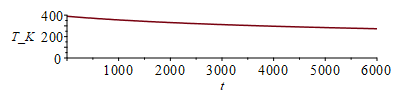 |
i.e. el periodo orbital es de unos 5830 s (1,6 h), durando el eclipse unos 2190 s (0,6 h), y siendo el tiempo de relajación térmica mucho mayor, tc=22 000 s (6 h) para que el satélite se enfríe desde 390 K hasta la mitad. En los 2190 s que dura el eclipse solo se enfriaría desde 390 K hasta 327 K.
h) Determinar la evolución de las temperaturas a lo largo de la órbita en el estado periódico.
Ponemos unas condiciones iniciales cualesquiera (e.g. TAB=TC=300 K) y vamos integrando las dos ecuaciones hasta el régimen periódico.
| > | 'eqC_'=eqC_;'eqAB_'=eqAB_;TCprime:=rhs(eqC_)/subs(dat,SI0,mC_*c[alu]);TABprime:=rhs(eqAB_)/subs(dat,SI0,mAB_*cB);; |
 |
  |
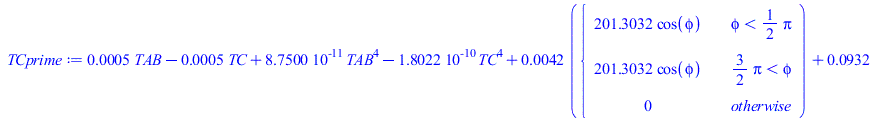 |
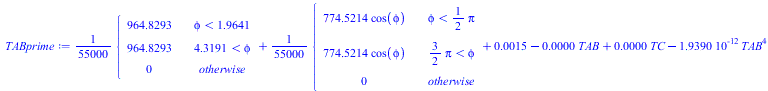 |
Vamos a ir integrando estas N=2 ecuaciones diferenciales acopladas por el método de Euler con un valor inicial arbitrario TC=TAB=300 K. Elegimos un paso temporal de Dt=10 s y un tiempo total de simulatión de Nc=4 órbitas (unos M=2300 pasos temporales) a ver si llegamos ya al régimen periódico.
| > | Tc:=273:Nc:=4;Dt:=10;M:=floor(Nc*(To_/s_)/Dt);N:=2;T0:=300;Ts:=Matrix(1..N,1..M,T0):pl1:=[0,T0-Tc]:pl2:=[0,T0-Tc]:for j from 1 to M-1 do t:=j*Dt;phi_:=t*2*Pi*s_/To_;Ts[1,j+1]:=Ts[1,j]+Dt*evalf(subs(phi=phi_,TC=Ts[1,j],TAB=Ts[2,j],TCprime));Ts[2,j+1]:=Ts[2,j]+Dt*evalf(subs(phi=phi_,TC=Ts[1,j],TAB=Ts[2,j],TABprime));;pl1:=pl1,[(j*Dt-Dt)*s_/To_,Ts[1,j]-Tc];pl2:=pl2,[(j*Dt-Dt)*s_/To_,Ts[2,j]-Tc];od:plot([[pl1],[pl2]]); |
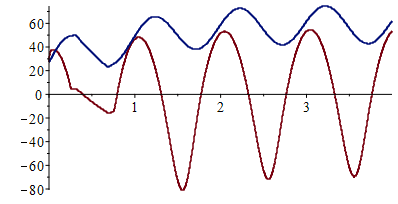 |
El cuarto ciclo ya parece periódico. Como el periodo orbital es 5830 s, cada órbita son Mo=To/Dt=583 saltos temporales, luego, el 4º periodo será desde j=3·583=1749 hasta j=4·583=2332.
| > | plot([[op(1749..2332,[pl1])],[op(1749..2332,[pl2])]]);q:=seq(op(2,op(i,[pl2])),i=1749..2332):TABmax=max([q])*`ºC`;TABmean=convert([q],`+`)/nops([q])*`ºC`;TABmin=min([q])*`ºC`;q:=seq(op(2,op(i,[pl1])),i=1749..2332):TCmax=max([q])*`ºC`;TCmean=convert([q],`+`)/nops([q])*`ºC`;TCmin=min([q])*`ºC`; |
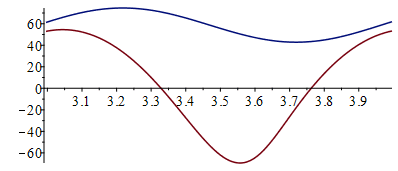 |
i.e. el conjunto A+B está casi todo el tiempo a más de los 50 ºC prescritos de máxima, y hay que rediseñarlo térmicamente.
i) Rediseñar los paneles C si fuera necesario.
Vemos que hay que bajar la temperatura media del conjunto A+B, que ahora es de casi 59 ºC y convendría que no superase los 35 ºC (para que el máximo no pasara de 50 ºC). La solución que parece más sencilla es aumentar la conductancia térmica entre A+B y las placas base C, con lo que se acercarían entre sí las temperaturas TAB y TC, por ejemplo añadiendo algunas cintas de cobre (o trenzas) en los rincones entre B y C. Si no fuera suficiente, podría disponerse un tubo de calor (heat pipe) que extrajera más eficazmente calor de A+B.
| > |
| > |