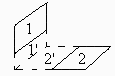
| > | restart:#"m13_p61.mw" |
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):with(plots): |
Consider the radiative coupling between two equal-size plates (1 and 2 in Fig. 1) of 0.25·0.50 m2. The plates are separated 0.25 m from the common line of their corresponding planes. Plate 1 has =0,6 y =0,8 at both faces, and gets 800 W/m2 normal to its external face (from a collimated source), whereas plate 2 has =0,5 at its upper face, and =0,8 at the lower one. Find:
a) All the view factors involved.
b) The required power to be applied to plate 2 in order to keep it at 20 ºC in an environment that may either be at 2.7 K or at 15 ºC.
c) Temperature of plate 1 in each case.
Considérese la radiación térmica entre las placas 1 y 2 de la Fig. 1. Ambas placas son de 0,25·0,50 m2, y están desplazadas 0,25 m respecto a la línea de intersección de los planos que las contienen. La placa 1 tiene =0,6 y =0,8 por ambas caras, y por su cara exterior absorbe 800 W/m2 de radiación perpendicular (proveniente de una fuente colimada), mientras que la placa 2 tiene =0,5 por la cara superior y =0,8 por la inferior. Se pide:
a) Factores geométricos.
b) Potencia necesaria para mantener la placa 2 a 20 ºC en un entorno a 2,7 K, y en un entorno a 15 ºC.
c) Temperaturas de la placa 1 en cada caso.
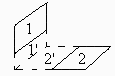
| > | dat:=[A1=0.25*0.50*m_^2,A2=0.25*0.50*m_^2,alpha1=0.6,epsilon1e=0.8,epsilon1i=0.8,E1=800*W_/m_^2,epsilon2i=0.5,epsilon2e=0.8,T2=(20+273.15)*K_,Tinf1=2.7*K_,Tinf2=(15+273.15)*K_];dat:=op(dat),Const,SI2,SI1: |
Uncheck this line to check for blackbody limit.
| > | #dat:=[A1=0.25*0.50*m_^2,A2=0.25*0.50*m_^2,alpha1=1,epsilon1e=0.999,epsilon1i=0.999,E1=800*W_/m_^2,epsilon2i=0.999,epsilon2e=0.999,T2=(20+273.15)*K_,Tinf1=2.7*K_,Tinf2=(15+273.15)*K_];dat:=op(dat),Const,SI2,SI1: |
a) All the view factors involved.
It may help finding the two-dimensional limit by the crossing-string method:
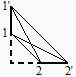
We may take as unit length the 0.25 m (homothecy)
| > | eqF12:=F12=(L12p+L1p2-L12-L1p2p)/(2*L11p);eqF12:=F12=(2*sqrt(5)-sqrt(2)-sqrt(8))/2;eqF12_:=evalf(%); |
i.e. if the rectangles were very large in z-dimension, F12=0.11. As they have only double z-span than profile span, F12 will be smaller.
The 3D-case can be found in VF-Tables: From horizontal rectangle of W·L to adjacent vertical rectangle of H·L, with h=H/L and w=W/L.
| > | F12:=(1/(Pi*w))*(w*arctan(1/w)+h*arctan(1/h)-sqrt(w^2+h^2)*arctan(1/sqrt(w^2+h^2))+ln(a*b^(w^2)*c^(h^2))/4);a:=(1+w^2)*(1+h^2)/(1+w^2+h^2);b:=w^2*(1+w^2+h^2)/((1+w^2)*(w^2+h^2));c:=h^2*(1+h^2+w^2)/((1+h^2)*(h^2+w^2));h=1,w=1;F22p_11p:=evalf(subs(w=1,h=1,F12));h=1/2,w=1/2;F2p_1p:=evalf(subs(w=1/2,h=1/2,F12));h=1,w=1/2;F2p_11p:=evalf(subs(w=1/2,h=1,F12));h=1/2,w=1;F22p_1p:=evalf(subs(w=1,h=1/2,F12));eqF:=F1_2=F1_22p-F1_2p;eqF:=F1_2=(A22p/A1)*F22p_1-(A2p/A1)*F2p_1;F12:='F12':eqF12:=F12='(A22p/A1)*(F22p_11p-F22p_1p)-(A2p/A1)*(F2p_11p-F2p_1p)';eqF12_:=subs(A22p=2*A1,A2p=A1,eqF12); |
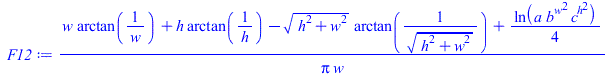 |
i.e. the real VF is F12=0.06 instead of the F12=0.11 2D-limit.
b) The required power to be applied to plate 2 in order to keep it at 20 ºC in an environment that may either be at
Blackbody model:
It may help to first solve the simpler blackbody case, to have a check point for the grey-surface exitance procedure to be developed.
| > | eqEB:=Qin=Qout;eqEB1:=A1*E1=A1*(M1bb-Minf)+A1*F12*(M1bb-M2bb)+A1*(1-F12)*(M1bb-Minf);eqEB2:=A1*F12*(M1bb-M2bb)+Wdis2=A2*(M2bb-Minf)+A2*(1-F21)*(M2bb-Minf);eqT2:=M2bb=sigma*T2^4;eqT2_:=subs(dat,%);eqEB1_:=subs(eqF12_,eqT2_,dat,eqEB1);eqEB2_:=subs(F21=F12,eqF12_,eqT2,dat,eqEB2); |
If Tinf=2.7 K:
| > | eqEB1__:=subs(Minf=sigma*Tinf1^4,dat,SI0,eqEB1_);eqEB2__:=subs(Minf=sigma*Tinf1^4,dat,SI0,eqEB2_);sol1:=solve({eqEB1__,eqEB2__},{M1bb,Wdis2});T1_:=evalf(subs(sol1,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%); |
i.e. in the BB-case with Tinf=2.7 K, plate 1 attains 19 ºC and plate 2 needs 102 W to be kept at 20 ºC, as can be checked by a single plate at 20 ºC (2·A·s·T^4=0.25·5.67e-8·293^4=105 W).
If Tinf=15 ºC:
| > | eqEB1__:=subs(Minf=sigma*Tinf2^4,dat,SI0,eqEB1_);eqEB2__:=subs(Minf=sigma*Tinf2^4,dat,SI0,eqEB2_);sol1:=solve({eqEB1__,eqEB2__},{M1bb,Wdis2});T1_:=evalf(subs(sol1,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%); |
i.e. in the BB-case with Tinf=15 ºC, plate 1 attains 71 ºC and plate 2 needs 1 W to be kept at 20 ºC.
For the real gey-surface-case we start by drawing the thermal-resistance circuit, guided by the general nodal equations.
| > | c:='c':eq13_10;eq13_11;eq13_12; |
![Q[1, rad] = `/`(`*`(epsilon[1], `*`(A[1], `*`(`+`(M[1, bb], `-`(M[1]))))), `*`(`+`(1, `-`(epsilon[1]))))](images/p61_41.gif) |
![Q[1, rad] = Sum(`*`(A[1], `*`(F[1, j], `*`(`+`(M[j], `-`(M[1]))))), j = 1 .. N)](images/p61_42.gif) |
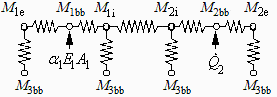
At node 1bb there are three flows: the input a1E1A1, and the two outputs towards 1e (exterior) and 1i (interior). Combining the two resistances in series from M1bb to M2bb we get:
| > | eq1bb:=alpha[1,e]*E[1]*A[1]=epsilon[1,e]*A[1]*(M[1,bb]-M[3,bb])+epsilon[1,i]*A[1]*(M[1,bb]-M[1,i])/(1-epsilon[1,i]);eq1bb_:=subs(alpha[1,e]=alpha1,epsilon[1,e]=epsilon1e,epsilon[1,i]=epsilon1i,E[1]=E1,A[1]=A1,dat,SI0,eq1bb);eqT2:=M[2,bb]=sigma*T2^4;eqT2_:=subs(dat,%); |
![Typesetting:-mprintslash([eq1bb := `*`(alpha[1, e], `*`(E[1], `*`(A[1]))) = `+`(`*`(epsilon[1, e], `*`(A[1], `*`(`+`(M[1, bb], `-`(M[3, bb]))))), `/`(`*`(epsilon[1, i], `*`(A[1], `*`(`+`(M[1, bb], `-`...](images/p61_45.gif) |
At node 1i
| > | eq1i:=epsilon[1,i]*A[1]*(M[1,bb]-M[1,i])/(1-epsilon[1,i])=A[1]*F[12]*(M[1,i]-M[2,i])+A[1]*(1-F[12])*(M[1,i]-M[3,bb]);eq1i_:=subs(alpha[1,e]=alpha1,epsilon[1,e]=epsilon1e,epsilon[1,i]=epsilon1i,E[1]=E1,A[1]=A1,F[12]=F12,eqF12_,dat,SI0,eq1i); |
![Typesetting:-mprintslash([eq1i := `/`(`*`(epsilon[1, i], `*`(A[1], `*`(`+`(M[1, bb], `-`(M[1, i]))))), `*`(`+`(1, `-`(epsilon[1, i])))) = `+`(`*`(A[1], `*`(F[12], `*`(`+`(M[1, i], `-`(M[2, i]))))), `*...](images/p61_49.gif) |
At node 2i
| > | eq2i:=A[1]*F[12]*(M[1,i]-M[2,i])=A[2]*(1-F[12])*(M[2,i]-M[3,bb])+epsilon[2,i]*A[2]*(M[2,i]-M[2,bb])/(1-epsilon[2,i]);eq2i_:=subs(alpha[1,e]=alpha1,epsilon[1,e]=epsilon1e,epsilon[2,i]=epsilon2i,E[1]=E1,A[1]=A1,F[12]=F12,eqF12_,A[2]=A2,eqT2_,dat,SI0,eq2i); |
![Typesetting:-mprintslash([eq2i := `*`(A[1], `*`(F[12], `*`(`+`(M[1, i], `-`(M[2, i]))))) = `+`(`*`(A[2], `*`(`+`(1, `-`(F[12])), `*`(`+`(M[2, i], `-`(M[3, bb]))))), `/`(`*`(epsilon[2, i], `*`(A[2], `*...](images/p61_51.gif) |
At node 2bb we combine the two resistances in series, as in node 1bb.
| > | eq2bb:=epsilon[2,i]*A[2]*(M[2,i]-M[2,bb])/(1-epsilon[2,i])+W[dis,2]=epsilon[2,i]*A[2]*(M[2,bb]-M[3,bb]);eq2bb_:=subs(alpha[1,e]=alpha1,epsilon[1,e]=epsilon1e,epsilon[2,i]=epsilon2i,E[1]=E1,A[1]=A1,F[12]=F12,eqF12_,A[2]=A2,eqT2_,dat,SI0,eq2bb); |
![Typesetting:-mprintslash([eq2bb := `+`(`/`(`*`(epsilon[2, i], `*`(A[2], `*`(`+`(M[2, i], `-`(M[2, bb]))))), `*`(`+`(1, `-`(epsilon[2, i])))), W[dis, 2]) = `*`(epsilon[2, i], `*`(A[2], `*`(`+`(M[2, bb]...](images/p61_53.gif) |
Once the set of 4 equations with 4 unknowns (M1bb,M1,M2) and the parameter M3bb=s·Tinf^4 been established, the solution is:
For Tinf=2.7 K:
| > | eqT3_:=M[3,bb]=subs(dat,sigma*Tinf1^4);sol1_:=solve(subs(eqT3_,SI0,{eq1bb_,eq1i_,eq2i_,eq2bb_}),{M[1,bb],M[1,i],M[2,i],W[dis,2]});T1_:=evalf(subs(sol1_,dat,SI0,(M[1,bb]/sigma)^(1/4)))*K_;'T1_'=TKC(%); |
i.e. for the grey case in space, plate 1 attains -2 ºC and plate 2 needs 51 W of heating.
For Tinf=20 ºC:
| > | eqT3_:=M[3,bb]=subs(dat,sigma*Tinf2^4);sol1_:=solve(subs(eqT3_,SI0,{eq1bb_,eq1i_,eq2i_,eq2bb_}),{M[1,bb],M[1,i],M[2,i],W[dis,2]});T1_:=evalf(subs(sol1_,dat,SI0,(M[1,bb]/sigma)^(1/4)))*K_;'T1_'=TKC(%); |
and for the grey case in a 20 ºC room (under vacuum), plate 1 attains 59 ºC and plate 2 needs 3 W of heating.
| > |