>	restart:#"m13_p54"

Considérese un cuerpo esférico de radio R0 que debe disipar una potencia fija P a un recinto evacuado muy grande (e.g. una esfera de radio mucho mayor, donde se ha hecho el vacío) a temperatura T∞. Se pide:

a) Temperatura superficial del cuerpo, T0, al interponer una delgada cáscara esférica concéntrica entre el cuerpo y el recinto (manteniendo todo evacuado), en función del radio de la cáscara, R1, y de las propiedades termoópticas.

b) Simplificación para el caso de cuerpos negros.

c)Aplicación numérica para R0=5 m, 0=0,7, P=100 kW, R1=6 m,1,int=0,8,1,ext=0,9, y T∞=2.7 K.

Datos:

>	with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(R0>0,epsilon0>0,R1>0,epsilon1int>0,epsilon1ext>0,P>0,Tinf>0,sigma>0,p>0,r>0):

>	su:="":dat:=[R0=5*m_,epsilon0=0.7,P=1e5*W_,R1=6*m_,epsilon1int=0.8,epsilon1ext=0.9,Tinf=2.7*K_];

Las ecuaciones de la transmisión de calor por radiación entre dos superficies, donde la segunda rodea completamente a la primera), pueden ser

>	eq13_4;eq13_5;eq13_6;dat:=op(dat),Const,SI2,SI1:

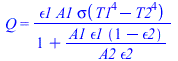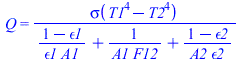	(1)

a) Temperatura superficial del cuerpo, T0, al interponer una delgada cáscara esférica concéntrica entre el cuerpo y el recinto (manteniendo todo evacuado), en función del radio de la cáscara, R1, y de las propiedades termoópticas.

Primero resolveremos el problema sin cáscara. El balance energético de la esfera es:

>	eqBEsin:=Q0=-P;eqEBsin:=Q0=A0*epsilon0*sigma*(Tinf^4-T0sin^4);T0sin_:=(Tinf^4+P/(4*Pi*R0^2*epsilon0*sigma))^(1/4);

	(2)

donde basta poner eps0=1 para el modelo de cuerpo negro. Se ve que la T0sin crece con Tinf y con P, y es más pequeña para R0 grandes y e0 grandes.

La aplicación numérica con los datos mencionados al final, daría:

>	T0sin__:=evalf(subs(dat,SI0,T0sin_))*K_;T0sin_bb:=evalf(subs(epsilon0=1,dat,SI0,T0sin_))*K_;

	(3)

i.e. sin cáscara, la esfera debería alcanzar 299 K (274 K si fuese negra) para evacuar los 100 kW en régimen estacionario.

Ahora resolvemos el problema de la cáscara por fuera, que, independiente de cómo sea por dentro, ha de evacuar una potencia P.

>	eqBE1ext:=P=A1*epsilon1ext*sigma*(T1^4-Tinf^4);T1_:=(Tinf^4+P/(4*Pi*R1^2*epsilon1ext*sigma))^(1/4);

	(4)

La aplicación numérica con los datos mencionados al final, daría:

>	T1__:=evalf(subs(dat,SI0,T1_))*K_;

(5)

i.e. la cáscara ha de estar solo a 257 K para disipar los 100 kW (ahora el área es mayor).

Y ahora ya podemos determinar la T0 con cáscara. Como la F12=1 (factor de vista desde la esfera interior hacia el interior de la cáscara):

>	eqBE0:=Q0=-P;eqBE0:=P=sigma*(T0^4-T1^4)/((1-epsilon0)/(epsilon0*A0)+1/A0+(1-epsilon1int)/(epsilon1int*A1));eqBE0_:=subs(T1=T1_,A0=4*Pi*R0^2,A1=4*Pi*R1^2,%);

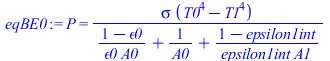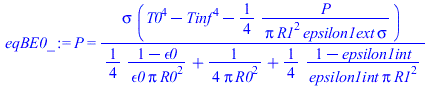	(6)

que nos da T0 en función de los datos.

b) Simplificación para el caso de cuerpos negros.

Basta hacer todos los eps=1.

LLamando r=R1/R0 y p=P/(A0*sigma), queda:

>	eqBE0_bb:=p=(T0^4-Tinf^4-p/r^2);T0bb_:=(Tinf^4+p+p/r^2)^(1/4);

	(7)

Puede verse en el límite r>>1 (cáscara muy lejana), se recupera el resultado sin cáscara (pero para cuerpo negro, claro):

>	T0bb_r_inf:=(Tinf^4+P/(4*Pi*R0^2*sigma))^(1/4);T0bb_r_inf_:=subs(dat,SI0,%)*K_;

	(8)

mientras que en el límite r<<1 (R1 muy próximo a R0) se tiene:

>	T0bb_r_1:=(Tinf^4+2*P/(4*Pi*R0^2*sigma))^(1/4);T0bb_r_1_:=subs(dat,SI0,%)*K_;

	(9)

i.e., si la cáscara está próxima a la esfera alcanzaría 323 K, y si está lejos 274 K, concluyéndose que los escudos radiativos conviene situarlos cerca para que aislen más.

c)Aplicación numérica para R0=5 m, 0=0,7, P=100 kW, R1=6 m,1,int=0,8,1,ext=0,9, y T∞=2.7 K.

Volviendo al caso general de cuerpos grises con la cáscara, tenemos:

>	eqBE0_:=subs(T0=T0con,eqBE0_);T0con_:=fsolve(subs(dat,SI0,%),T0con=100..1000)*K_;

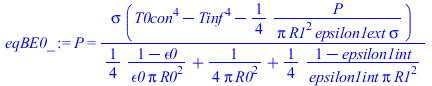	(10)

i.e. la esfera debe ponerse a 340 K si tiene la cáscara (sin cáscara estaba a 299 K).

>