| > | restart:#"m13_p51" |
Considérese un panel solar de 12 m2 desplegado en un satélite geoestacionario y orientado al Sol. El panel consta de una lámina de células solares de 30 % de rendimiento eléctrico y 0,5 mm de espesor (incluyendo la capa protectora antirreflectante y el adhesivo), pegada sobre un panel en nido de abeja formado por celdas hexagonales de 8 mm de separación, 25 m de espesor de lámina de aluminio (Al-5056), y 15 mm de altura entre capas de fibra de carbono (CFRP) de 0,25 mm de espesor. Con los datos de la Tabla adjunta, y despreciando la influencia del resto del satélite, calcular:
a) La temperatura estacionaria considerando dos nodos, despreciando la radiación dentro del panel.
b) Transmisión de calor por radiación interior en el panel suponiendo que la lámina de aluminio fuese especular, y comparación con la conducción del aluminio.
c) Para una celdilla del panel, factor geométrico entre las bases aproximando el prisma hexagonal por un cilindro.
d) Considerando que el prisma hexagonal fuese suficientemente esbelto para despreciar el efecto de las bases, determinar todos los factores geométricos entre sus caras.
e) Suponiendo conocidos todos los factores geométricos del prisma real (no infinitamente largo), y las temperaturas de las bases (T1 y T2), plantear las ecuaciones que permiten resolver el problema de tres nodos (i.e. base 1, caras laterales 3, y base 2), en el caso general de superficies grises, especificando las incógnitas.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(RealDomain): |
| > | dat:=[L1=1*m_,L2=2*m_,E=1370*W_/(m_^2*K_),eta=0.3,s=8e-3*m_,delta=25e-6*m_,Lh=15e-3*m_,Ls=0.5e-3*m_,Lc=0.25e-3*m_,Tinf=2.7*K_];datS:=k=100*W_/(m_*K_),rho=3500*kg_/m_^3,c=750*J_/(kg_*K_),alpha1=0.8,epsilon1=0.8;datC:=k=1*W_/(m_*K_),rho=1700*kg_/m_^3,c=850*J_/(kg_*K_),alpha2=0.3,epsilon2=0.8;datA:=k=120*W_/(m_*K_),rho=2700*kg_/m_^3,c=900*J_/(kg_*K_),alphaA=0.2,epsilonA=0.2;dat:=op(dat),Const,SI2,SI1: |

a) La temperatura estacionaria considerando dos nodos, despreciando la radiación dentro del panel.
Sea 1 el nodo delantero, que incluiría las células solares más la capa de CFRP más la mitad del honeycomb, aunque ésto solo importaría para los transitorios), y sea 2 el nodo trasero. La separación entre nodos sería la de los centros de masas respectivos, que podemos aproximar por la separación entre caras externas, Lp=Ls+Lc+Lh+Lc (p=panel, s=solarcells, c=carbonfibre, h=honeycomb).
| > | eqBE:=m*c*dT/dt=W+Q;eqBE1:=m1*c1*dT1/dt=(alpha1-eta*Fpq)*E*A-epsilon1*A*sigma*(T1^4-Tinf^4)-kp*A*(T1-T2)/Lp;eqBE2:=m2*c2*dT2/dt=kp*A*(T1-T2)/Lp-epsilon2*A*sigma*(T2^4-Tinf^4);A_:=subs(dat,L1*L2);eqBE1std:=0=(alpha1-eta*1)*E*A-epsilon1*A*sigma*(T1^4-Tinf^4)-kp*A*(T1-T2)/Lp;eqBE2std:=0=kp*A*(T1-T2)/Lp-epsilon2*A*sigma*(T2^4-Tinf^4);eqkp:=kp=Lp/(Ls/ks+Lc/kc+Lh/kh+Lc/kc);eqLp:=Lp=Ls+Lc+Lh+Lc;eqLp_:=subs(dat,%);eqkh:=kh=k*(8/3)*delta/s;eqkh_:=subs(datA,dat,%);eqkp_:=subs(ks=k,datS,kc=k,datC,eqkh_,eqLp_,dat,eqkp);T1_:=solve(eqBE2std,T1);T2_:=fsolve(subs(T1=T1_,A=A_,datS,datC,eqkp_,eqLp_,dat,SI0,eqBE1std),T2=100.500)[2]*K_;T1__:=subs(T2=T2_,A=A_,datS,datC,eqkp_,eqLp_,dat,T1_); |
 |
|
| (1) |
i.e. la cara iluminada quedaría a 297 K y la trasera a 292 K. Los valores de temperatura de trabajo aceptables para laos paneles solares suelen estar en el rango 200..350 K.
Podríamos haber aproximado la resistencia térmica global (s+c+h+c) por la del honeycomb (i.e. Lp=Lh y kp=kh) y los resultados serían prácticamente iguales
Si solo se hubiese tomado un nodo, este quedaría a una temperatura intermedia (295 K):
| > | eqBE12:=m12*c12*dT12/dt=(alpha1-eta*Fpq)*E*A-epsilon1*A*sigma*(T12^4-Tinf^4)-epsilon2*A*sigma*(T12^4-Tinf^4);(subs(dT12=0,A=A_,Fpq=1,datS,datC,eqkh_,dat,SI0,eqBE12));T12_:=solve(%,T12)[1]*K_; |
| (2) |
Para 2 nodos podríamos asumir que esa T12 sería la media, y calcular la diferencia T1-T2=DeltaT linealizando. Todavía más sencillo; tomando T2=T12 en la eqBE2, calculamos DeltaT directamente:
| > | eqBE2std;eqBE2std_:=subs(T1=T2+DeltaT,T2=T12,%);%;eqBE2std__:=subs(T12=T12_,eqkp_,eqLp_,A=A_,datC,dat,SI0,%);DeltaT_:=solve(%)*K_; |
| (3) |
que coincide sensiblemente con la diferencia de las temperaturas T1-T2=297,3-292,2=5,1 K.
b) Transmisión de calor por radiación interior en el panel suponiendo que la lámina de aluminio fuese especular, y comparación con la conducción a lo largo del aluminio.
Si las láminas de aluminio son especulares (a=e=0), sería cono si no existieran (despreciando el área transversal ocupada, Aalu/Atotal=(8/3)·(delta/s)=0,008).
Se trata del intercambio radiativo entre las dos caras interiores del CFRP:
| > | Qradh0e:=fe*L1*L2*sigma*(T1^4-T2^4);fe:=1/((1-epsilon1)/epsilon1+1+(1-epsilon2)/epsilon2);Qradh0e_:=subs(T1=T1__,T2=T2_,epsilon1=epsilon2,datC,dat,Qradh0e);Qcondh:=kh*L1*L2*(T1-T2)/Lh;Qconh_:=subs(eqkh_,T1=T1__,T2=T2_,dat,%);Qradh01:=L1*L2*sigma*(T1^4-T2^4);Qradh01_:=subs(T1=T1__,T2=T2_,dat,%); |
 |
|
| (4) |
i.e. por radiación de calor se transmiten 40 W y por conducción de calor 680 W. Si se hubieran considerado las propiedades termoópticas reales de la lámina de aluminio (no especular), la contribución radiativa hubiese sido todavía más pequeña (haría un pequeño efecto de escudo radiativo). Incluso si el CFRP fuese cuerpo negro solo se íntercambiarían 60 W por radiación, por lo que a partir de aquí despreciaremos la radiación interior frente a la conducción.
c) Para una celdilla del panel, factor geométrico entre las bases aproximando el prisma hexagonal por un cilindro.
Conviene usar un círcula de igual área, aunque el círculo inscrito o el circunscrito darían resultados parecidos.
De la Tabla (caso 'Base to finite cylinder'):
| > | F13:=1-rho/(2*r);rho:=(sqrt(4*r^2+1)-1)/r;r:=R/H;eqR:=Pi*R^2=sqrt(3)*s^2/2;R_:=solve(subs(dat,%),R)[2];r_:=subs(dat,R_/Lh);rho_:=subs(R=R_,H=Lh,dat,rho);F13_:=subs(R=R_,H=Lh,dat,F13); |
| (5) |
i.e. en nuestro caso F12=0,07 (entre las bases a T1 y T2). La aproximación de los hexágonos por cuadrados hubiera sido peor, pero tampoco muy distinta:
Caso cuadrado. De la Tabla (caso 'Equal square plates'):
| > | F12:=(1/(Pi*w^2))*(ln(x^4/(1+2*w^2))+4*w*y);x:=sqrt(1+w^2);y:=x*arctan(w/x)-arctan(w);w:=W/H;eqW:=W^2=sqrt(3)*s^2/2;W_:=evalf(subs(dat,SI0,sqrt(sqrt(3)*s^2/2)))*m_;w_:=subs(dat,W_/Lh);y_:=subs(W=W_,H=Lh,dat,y);x_:=subs(W=W_,H=Lh,dat,x);F12__:=evalf(subs(W=W_,H=Lh,dat,F12)); |
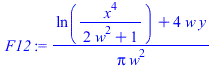 |
|
| (6) |
d) Considerando que el prisma hexagonal fuese suficientemente esbelto para despreciar el efecto de las bases, determinar todos los factores geométricos entre sus caras.
Fij hexágono bidimensional. De la Tabla (casos 'Equal adjacent strips' y 'Strip to strop'): 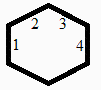
| > | F12adyacente:=1-sin(alpha/2);F12adyacente:=1-sqrt(3)/2;evalf(%);F12frontal:=sqrt(1+h^2)-h;F12frontal:=2-sqrt(3);evalf(%);eqFsum:='F12frontal+2*F12adyacente+2*F12otro=1';F12otro:='(1-F12frontal)/2-F12adyacente';evalf(%); |
| (7) |
i.e. de una cara a la adyacente a 120º, F12=0,13. De una cara a la de enfrente, F12=0,27. Y de una cara a la que no está enfrente ni contigua, F12=0,23 (obtenida por la relación de completitud SumF1j=1).
e) Suponiendo conocidos todos los factores geométricos del prisma real (no infinitamente largo), y las temperaturas de las bases (T1 y T2), plantear las ecuaciones que permiten resolver el problema de tres nodos (i.e. base 1, caras laterales 3, y base 2), en el caso general de superficies grises, especificando las incógnitas.
Por el método de las exitancias, las incógnitas serán las exitancias M1 y M2, cuyas emitancias de cuerpo negro soon conocidas (M1bb=sigma*T1^4, M2bb=sigma*T2^4), y las dos incógnitas de las caras laterales, M3 y M3bb(que será sigma*T3^4 pero desconocemos T3). Y las 4 ecuaciones son:
| > | A1:='A1':T1:='T1':T2:='T2':F12:='F12':F13:='F13':eq1:=epsilon1*A1*(M1-M1bb)/(1-epsilon1)=A1*F12*(M2-M1)+A1*F13*(M3-M1);eq2:=epsilon2*A2*(M2-M2bb)/(1-epsilon2)=A2*F21*(M1-M2)+A2*F23*(M3-M2);eq3:=epsilon3*A3*(M3-M3bb)/(1-epsilon3)=A3*F31*(M1-M3)+A3*F32*(M2-M3);eq4:=0=rhs(eq3); |
| (8) |
donde la eq4 establece la adiabaticidad lateral.
Para los Fij podríamos usar los aquí calculados: F12=0,07, F13=1-0,07=0,93. En la Red pueden encontarse valores más precisos de Fij para prismas hexagonales.
Si resolvemos el sistema:
| > | datF:=F12=0.07,F13=0.93,F21=0.07,F23=0.93;F31:=A1*F13/A3;A1:=rhs(eqR);A1_:=evalf(subs(dat,rhs(eqR)));A3:=6*Lh*s/sqrt(3);A3_:=evalf(subs(dat,%));A2:=A1;F31_:=subs(datF,A1_*F13/A3_);datM:=M1bb=sigma*T1^4,M2bb=sigma*T2^4;datE:=epsilon1=epsilon2,epsilon2=epsilon2,epsilon3=epsilon2;eq1_A1:=evalf(subs(datM,T1=T1__,T2=T2_,datE,datF,F31=F31_,F32=F31_,A1=A1_,A3=A3_,datC,dat,SI0,eq1/A1_));eq2_A2:=evalf(subs(datM,T1=T1__,T2=T2_,datE,datF,F31=F31_,F32=F31_,A1=A1_,A3=A3_,datC,dat,SI0,eq2/A1_));eq3_A3:=evalf(subs(datM,T1=T1__,T2=T2_,datE,datF,F31=F31_,F32=F31_,A1=A1_,A3=A3_,datC,dat,SI0,eq3/A3_));eq4_A3:=evalf(subs(datM,T1=T1__,T2=T2_,datE,datF,F31=F31_,F32=F31_,A1=A1_,A3=A3_,datC,dat,SI0,eq4/A3_));sol_:=solve({eq1_A1,eq2_A2,eq3_A3,eq4_A3},{M1,M2,M3,M3bb});eqM3bb:=M3bb=sigma*T3^4;T3_:=subs(sol_,dat,SI0,sqrt(sqrt((M3bb/sigma))))*K_; |
| (9) |
i.e. la lámina de aluminio quedaría a 295 K (a una temperatura intermedia entre T1 y T2, como era de esperar).
| > |