| > | restart:#"m13_p46" |
Se quiere estudiar la radiación térmica intercambiada entre dos placas iguales, de 400501 cm3, ambas pintadas de blanco, dispuestas verticalmente como indica la figura, siendo L=50 cm y L0=0,25 m. Ambas placas están soportadas convenientemente en un gran recinto y rodeadas de aire ambiente a 20 ºC, con el que el coeficiente de convección térmica se supondrá igual a 10 W/(m2•K). Sabiendo que la placa vertical se mantiene permanentemente a 120 ºC mediante una resistencia eléctrica interna, se pide
a) Potencia disipada en la resistencia, despreciando el efecto de la otra placa.
b) Se va a estimar el factor geométrico entre ambas placas en el límite bidimensional (400 cm >> 50 cm), habiéndose encontrado en una recopilación que el factor geométrico desde una banda horizontal L1 a una banda vertical L2 con vértice común en el origen es , siendo r≡ L2/L1 la relación de anchuras. ¿A qué valor tiende F12 cuando L1<<L2? Razonar físicamente la respuesta.
c) Con el modelo anterior, determinar el factor geométrico entre ambas placas (en el límite bidimensional).
d) Temperatura que alcanzaría la placa horizontal en régimen estacionario con el modelo de cuerpos negros.
e) Temperatura que alcanzaría la placa horizontal en régimen estacionario con la pintura descrita.
Datos:
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | dat:=[Lz=4*m_,L=0.5*m_,Lw=0.01*m_,L0=0.25*m_,alpha=0.20,epsilon=0.85,X=0.25*m_,T0=(20+273.15)*K_,h=10*W_/(m_^2*K_),T2=(120+273.15)*K_];eqF:=F12=(1+r-sqrt(1+r^2))/2;eqr:=r=L2/L1; |
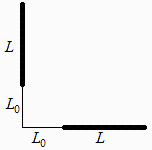
We assume usual thermo-optical properties for paints.
Eqs. const.:
| > | dat:=op(dat),Const,SI2,SI1: |
a) Potencia disipada en la resistencia, despreciando el efecto de la otra placa.
Pla 2 (vertical). Balance energético (despreciamos las áreas de los bordes):
| > | eqEB:=m2*c2*dT2/dt=Wdis-h*2*A*(T2-T0)-epsilon*2*A*sigma*(T2^4-T0^4);eqA:=A=L*Lz;eqA_:=subs(dat,%);Wdis_:=subs(eqA,dat,epsilon*2*A*sigma*(T2^4-T0^4)+h*2*A*(T2-T0));eqA_:=A=L*Lz+L*Lw+Lz*Lw;Wdis_:=subs(eqA_,dat,epsilon*2*A*sigma*(T2^4-T0^4)+h*2*A*(T2-T0)); |
| (1) |
i.e. la resistencia disipa 7,3 kW (nótese que la diferencia si se añadien los bordes es del 2%).
b) Se va a estimar el factor geométrico entre ambas placas en el límite bidimensional (400 cm >> 50 cm), habiéndose encontrado en una recopilación que el factor geométrico desde una banda horizontal L1 a una banda vertical L2 con vértice común en el origen es , siendo r≡ L2/L1 la relación de anchuras. ¿A qué valor tiende F12 cuando L1<<L2? Razonar físicamente la respuesta.
| > | eqF;eqF_rinf:=F12=asympt(rhs(eqF),r,2); |
| (2) |
i.e. cuando L2/L1 tiende a infinito, F12 tiende a 1/2. Físicamente, se trata de calcular la fracción, de toda la emisión de una pequeña placa horizontal, que incide sobre el plano vertical adyacente, que, si se consideran la placa encajonada entre sus dos planos perpendiculares adyacentes, se ve que por simetría la mitad va a cada lado (el escape por el cénit es despreciable).
c) Con el modelo anterior, determinar el factor geométrico entre ambas placas (en el límite bidimensional).
Se obtiene aplicando el álgebra de los factores geométricos. Sea F1p2p el factor geométrico desde la superficie 1' hasta la superficie 2', y F11p22p el
| > | F12=F122p-F12p;F12=(A22p/A1)*F22p1-(A2p/A1)*F2p1;F12=(A22p/A1)*(F22p11p-F22p1p)-(A2p/A1)*(F2p11p-F2p1p);eqr_1p2p:=r=L0/L0;eqr_11p22p:=r=(L0+L)/(L0+L);F1p2p_:=subs(%,rhs(eqF));F1p2p__:=evalf(%);F2p1p__:=%;F11p22p_:=F1p2p__;F22p11p_:=%;eqr_1p22p:=r=(L0+L)/L0;eqr_1p22p_:=evalf(subs(dat,%));F1p22p_:=subs(%,rhs(eqF));F2p11p_:=%;eqr_11p2p:=r=L0/(L0+L);eqr_11p2p_:=evalf(subs(dat,%));F11p2p_:=subs(%,rhs(eqF));F22p1p_:=%;A1:=L*Lz;A2p:=L0*Lz;A22p:=(L0+L)*Lz;F12_:=subs(dat,(A22p/A1)*(F22p11p_-F22p1p_)-(A2p/A1)*(F2p11p_-F2p1p__)); |
| (3) |
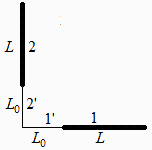
i.e. F12=0,17 (i.e. el 17% de lo que emite la cara derecha de la placa vertical alcanza la cara superior de la placa horizontal.
d) Temperatura que alcanzaría la placa horizontal en régimen estacionario con el modelo de cuerpos negros.
| > | eqBE1:=A*F12*sigma*(T2^4-T1^4)-A*(1-F12)*sigma*(T1^4-T0^4)-A*sigma*(T1^4-T0^4)-2*A*h*(T1-T0);eqBE2:=Wdis-A*F12*sigma*(T2^4-T1^4)-A*(1-F12)*sigma*(T2^4-T0^4)-A*sigma*(T2^4-T0^4)-2*A*h*(T2-T0);sol_:=fsolve(subs(F12=F12_,eqA,dat,SI0,{eqBE1,eqBE2}),{T1,Wdis},T1=100..1000); |
| (4) |
i.e. la placa horizontal se calienta desde los 20 ºC del entorno hasta 25 ºC (298 K). Con este modelo de cuerpo negro la resistencia debería aportar más energía que antes (7,7 kW en vez de 7,3 kW).
e) Temperatura que alcanzaría la placa horizontal en régimen estacionario con la pintura descrita.
Se apica el método de las exitancias (Fig. 3) estableciendo el balance de energía en cada nudo de la red. Tomando la resistencia combinada de las dos resistencias en serie en cada extremo, quedan solo 4 nudos (cuatro ecuaciones) con 4 incógnitas: M2bb,M2i,M1i,M1bb:
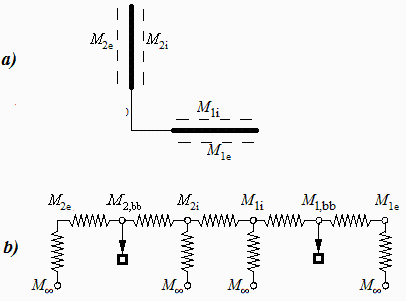
Fig. 3. Circuito equivalente para el cálculo de exitancias M.
| > | eqM2bb:=(M0-M2bb)/(1/(A*F2e0)+(1-epsilon)/(A*epsilon))+(M2i-M2bb)/((1-epsilon)/(A*epsilon))=m2*c2*dT2/dt-Wdis-2*A*h*(T0-T2);eqM2i:=(M2bb-M2i)/((1-epsilon)/(A*epsilon))+(M1i-M2i)*A*F12+(M0-M2i)*A*(1-F12)=0;eqM1i:=(M2i-M1i)*A*F12+(M0-M1i)*A*(1-F12)+(M1bb-M1i)/((1-epsilon)/(A*epsilon))=0;eqM1bb:=(M1i-M1bb)/((1-epsilon)/(A*epsilon))+(M0-M1bb)/(1/(A*F1e0)+(1-epsilon)/(A*epsilon))=m1*c1*dT1/dt-2*A*h*(T0-T1);M0:=sigma*T0^4;M2bb:=sigma*T2^4;M1bb:=sigma*T1^4;sol_:=fsolve(subs(F2e0=1,F12=F12_,F1e0=1,eqA,dat,dT1=0,dT2=0,SI0,{eqM2bb,eqM2i,eqM1i,eqM1bb}),{Wdis,M2i,M1i,T1},{T1=290..300});T1_:=subs(%,T1*K_);'T1_'=TKC(%); |
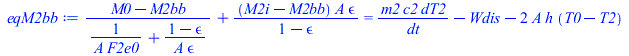 |
|
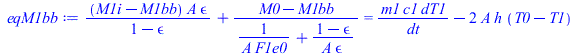 |
|
| (5) |
i.e. la placa horizontal alcanza 297 K (23,8 ºC, en vez de los 25 ºC que daba el modelo de cuerpo negro).
AÑADIDO.
Como se dispone del factor geométrico tridimensional, podemos ver cuánto se desvía el modelo bidimensional.(From horizontal rectangle of W·L to adjacent vertical rectangle of H·L, with h=H/L and w=W/L.).
| > | eqF:=F12=(1/(Pi*w))*(w*arctan(1/w)+h*arctan(1/h)-sqrt(w^2+h^2)*arctan(1/sqrt(w^2+h^2))+ln(a*b^(w^2)*c^(h^2))/4);a:=(1+w^2)*(1+h^2)/(1+w^2+h^2);b:=w^2*(1+w^2+h^2)/((1+w^2)*(w^2+h^2));c:=h^2*(1+h^2+w^2)/((1+h^2)*(h^2+w^2)); |
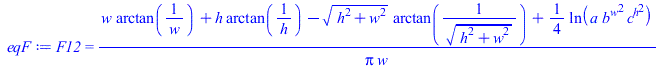 |
|
| (6) |
| > | eqr:=w=L/Lz,h=L/Lz;eqr:=w=subs(dat,L/Lz),h=subs(dat,L/Lz);eqr:=w=(L0+L)/Lz,h=(L0+L)/Lz;eqr:=w=subs(dat,(L0+L)/Lz),h=subs(dat,(L0+L)/Lz); |
| (7) |
| > | F12=F122p-F12p;F12=(A22p/A1)*F22p1-(A2p/A1)*F2p1;F12=(A22p/A1)*(F22p11p-F22p1p)-(A2p/A1)*(F2p11p-F2p1p);eqr_1p2p:=w=L0/Lz,h=L0/Lz;eqr_1p2p:=w=subs(dat,L0/Lz),h=subs(dat,L0/Lz);eqr_11p22p:=w=(L0+L)/Lz,h=(L0+L)/Lz;eqr_11p22p:=w=subs(dat,(L0+L)/Lz),h=subs(dat,(L0+L)/Lz);F1p2p_:=subs(%,rhs(eqF));F1p2p__:=evalf(%);F2p1p__:=%;F11p22p_:=F1p2p__;F22p11p_:=%;eqr_1p22p:=w=L0/Lz,h=(l0+L)/Lz;eqr_1p22p_:=w=subs(dat,L0/Lz),h=subs(dat,(L0+L)/Lz);F1p22p_:=evalf(subs(%,rhs(eqF)));F2p11p_:=%;eqr_11p2p:=w=(L0+L)/Lz,h=L0/Lz;eqr_11p2p_:=w=subs(dat,(L0+L)/Lz),h=subs(dat,L0/Lz);F11p2p_:=evalf(subs(%,rhs(eqF)));F22p1p_:=%;A1:=L*Lz;A2p:=L0*Lz;A22p:=(L0+L)*Lz;F12_:=subs(dat,(A22p/A1)*(F22p11p_-F22p1p_)-(A2p/A1)*(F2p11p_-F2p1p__)); |
| (8) |
i.e. en 3D es F12=0,14 (en 2D era F12=0,17; es casi un 20% menor).
| > | M0:=sigma*T0^4;M2bb:=sigma*T2^4;M1bb:=sigma*T1^4;sol_:=fsolve(subs(F2e0=1,F12=F12_,F1e0=1,eqA,dat,dT1=0,dT2=0,SI0,{eqM2bb,eqM2i,eqM1i,eqM1bb}),{Wdis,M2i,M1i,T1},{T1=290..300});T1_:=subs(%,T1*K_);'T1_'=TKC(%); |
| (9) |
i.e. en 3D la placa horizontal queda a T1=23,2 ºC (con el modelo 2D quedaba a 23,8 ºC).
| > |