p411.html

> restart:#"m13_p41"

Considérese un disco plano de 0,5 m de diámetro enfrentado al Sol en el vacío espacial, y entre ambos, separado un metro de distancia, otro disco igual y concéntrico, ambos de aluminio pintado de negro por ambas caras. Tómese una irradiancia solar de 1370 W/m2 y una temperatura de la radiación de fondo de 2,7 K. Se pide:

a) Determinar la temperatura que alcanzaría el primer disco en ausencia del segundo.

b) Calcular el factor geométrico entre los discos.

c) Plantear los balances energéticos para cada disco.

d) Determinar las temperaturas que alcanzarían los discos.

Data:

> read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

> dat:=[D=0.5*m_,L=1*m_,E=1370*W_/m_^2,T0=2.7*K_];A=Pi*D^2/4;

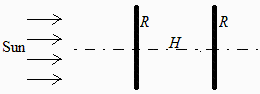
> dat:=op(dat),A=subs(dat,Pi*D^2/4),Const,SI2,SI1:

a) Determinar la temperatura que alcanzaría el primer disco en ausencia del segundo.

> eqEB:=C*dT/dt=alpha*E*A-epsilon*2*A*sigma*T^4;eqT:=T=(alpha*E/(2*epsilon*sigma))^(1/4);eqT_bb:=evalf(subs(alpha=1,epsilon=1,dat,eqT));

i.e. un disco solo quedaría a 332 K.

b) Calcular el factor geométrico entre los discos.

A partir de las Tablas de factores geométricos:

> F12:=1+1/(2*r^2)*(1-sqrt(4*r^2+1));eqr:=r=R/L;F12_:=subs(eqr,R=D/2,dat,F12);eqF:=F1e0=1,F1i2i=F12_,F1i0=1-F12_,F2i1i=F12_,F2i0=1-F12_,F2e0=1;

i.e. F12=0.056, que significa que sólo el 6% de la radiación que emite un disco por una cara llega al otro.

c) Plantear los balances energéticos para cada disco.

Tomando la radiación solar como unidireccional (aunque los efectos de la conicidad de los 0,01 rad que subtiende el disco solar ya serían apreciables para una esbeltez tan grande), los balances energéticos quedan:

> eqEB1:=C1*dT1/dt=E*A-A*sigma*T1^4-A*F1i2i*sigma*(T1^4-T2^4)-A*F1i0*sigma*T1^4;eqEB2:=C2*dT2/dt=A*F1i2i*sigma*(T1^4-T2^4)-A*F2i0*sigma*T2^4-A*sigma*T2^4;

d) Determinar las temperaturas que alcanzarían los discos.

> eqs:=evalf(subs(dT1=0,dT2=0,eqF,dat,SI0,[eqEB1,eqEB2]));sol_K_:=solve(eqs,[T1,T2])[1];

i.e. el disco de delante queda casi igual, a 332 K, y el disco de detrás queda a 135 K).