>	restart:#"m13_p29"

Consider a cubic enclosure 0.5 m in side, with its upper face a black-body at 400 K and its lower face a black-body at 300 K. Assume that there is only heat transfer by radiation (no convection and no conduction through the joins). Find the heat transfer to the bottom face under the following cases:

a) Assuming all lateral surfaces to be perfect mirrors.

b) Assuming all lateral surfaces to be perfect re-radiators (black-bodies externally insulated).

c) Assuming all lateral surfaces to be at 300 K as the bottom one.

d) Assuming all lateral surfaces to be kept cryogenic at 70 K.

Data:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(RealDomain):

>	dat:=[L=0.5*m_,T1=400*K_,T2=300*K_,T3=70*K_];

1=upper, 2=lower, 3=lateral.

>	dat:=op(dat),Const,SI2,SI1:

a) Assuming all lateral surfaces to be perfect mirrors.

Each surface has a face area A=0.25 m2. The view factor from the top surface to the bottom surface corresponds to two identical parallel square plates of side L=0.5 m and separation H=0.5 m, with a=L/H=1, resulting in a value F12=0.2. The four lateral surfaces can be jointly considered as surface 3.

If the lateral surfaces are perfect mirrors, the bottom surface sees the whole hemisphere uniformly radiating at 400 K, and the heat received by surface 2 is

>	Q2:=A2*F[2,13]*sigma*(T1^4-T2^4);eqA:=A=subs(dat,L^2);F[2,13]:=1;Q2_:=subs(A2=A,eqA,dat,Q2);

i.e. the bottom surface gets 248 W.

b) Assuming all lateral surfaces to be perfect re-radiators (black-bodies externally insulated).

If the lateral surface A3 is a perfect re-radiator, it must be at its steady state, balancing the input from the top with the output to the bottom, i.e. verifying Q3,in=Q3,out, which, based on the reciprocity relation A3F32=A2F23 and the symmetry of the problem (A2=A1, F23=F13), yields the relation for the adiabatic temperature, and finally the heat received by surface 2.

>

eqEB3:=0=A1*F13*(T1^4-T3^4)-A3*F32*(T3^4-T2^4);eqEB3:=0=(T1^4-T3^4)-(T3^4-T2^4);T3_:=((T1^4+T2^4)/2)^(1/4);T3__:=evalf(subs(dat,%));Q2:=A1*F12*sigma*(T1^4-T2^4)+A3*F32*sigma*(T3^4-T2^4);Q2:=A1*F12*sigma*(T1^4-T2^4)+A2*F23*sigma*(T3^4-T2^4);F12:=(ln(x^4/(1+2*w^2))+4*w*(x*arctan(w/x)-arctan(w)))/(Pi*w^2);x:=sqrt(1+w^2);w:=L/L;F12:=evalf(subs(w=1,F12));F13='1-F12';F13:=1-F12;F23:=F13;Q2_:=subs(A1=A,A2=A,eqA,T3=T3__,dat,Q2);

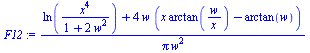i.e. now it gets 149 W instead of 248 W.

c) Assuming all lateral surfaces to be at 300 K as the bottom one.

If the lateral surfaces are at the same temperature than the bottom one, there is no heat transfer with them, and the heat received by surface 2 is just:

>	eqT3:=T3=subs(dat,T2);Q2_:=subs(A1=A,A2=A,eqA,eqT3,dat,Q2);

i.e. now it gets 50 W.

d) Assuming all lateral surfaces to be kept cryogenic at 70 K.

>	eqT3:=T3=subs(dat,T3);Q2_:=subs(A1=A,A2=A,eqA,eqT3,dat,Q2);

i.e. if the lateral walls are so cold, the bottom face loses 42 W, in spite of being frontal to a heated plate.

Notice the important effect of lateral-wall conditions on the top-down heat flow.

>