| > | restart:#"m13_p20" |
Determinar la hora solar a partir de la hora oficial (ecuación del tiempo).
Datos:
| > | read`../therm_const.m`:read`../therm_proc.m`:read`../therm_eq.m`:with(therm_proc): |
| > | dat:=[C1=7.5*60*s_,N1=184,C2=10*60*s_,N2=80]: |
Eqs. const.:
| > | dat:=op(dat),Const,SI2,SI1: |
a) Determinar la hora solar a partir de la hora oficial.
Aunque este problema parecer tener poca relación con la radiación térmica, no es así: En la Tierra, la fuente de radiación térmica más importante es el Sol, y la incidencia de esta radiación varía con la hora del día, así que es importante saber dónde está el Sol a una hora dada (de reloj). Bien es verdad que la diferencia entre la hora de reloj y la hora solar es muy pequeña, y sólo se logró medir con precisión a partir del siglo XVII con la invención del reloj de péndulo (los anteriores no eran muy precisos).
Hoy día, muchos mecanismos de apuntamiento solar ya disponen de software de control para corregir por este fenómeno (ecuación del tiempo).
La ecuación del tiempo calcula la diferencia entre la hora solar verdadera y la hora solar media (e.g. la hora de paso del Sol por el meridiano local, respecto al 'medidía de reloj').
La hora solar media es la que marca un buen reloj (e.g. reloj atómico) que acumulara 86400·365.242 segundos entre pasos consecutivos del sol por el equinoccio ascendente (año solar o año trópico; el año sidéreo dura unos 20.5 minutos más, debido al movimiento de traslación del Sol).
La hora solar media sería también la que correspondería a una órbita circular tierra-sol, que tendría 86400 s de periodo (e.g. entre mediodías).
Pero el movimiento real sol-tierra, con su excentricidad órbital y la inclinación del eje de rotación terrestre, hacen que la posición del sol visto desde la tierra se adelante o se retrase un poco a lo largo del año, respecto al reloj; i.e. el sol no pasa a las 12:00 por el meridiano local ni siquiera en Greenwich donde no hay correcciones por latitud ni longitud.
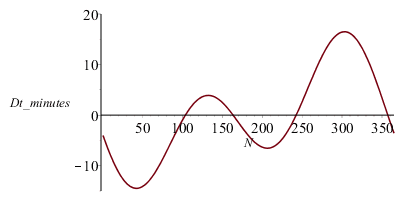
Una buena aproximación para la ecuación del tiempo es Dt=C1*sin(2*pi*(N-N1)/365)+C2*sin(4*pi*(N-N2)/365), con C1=7,5 minutos, C2=10 minutos, N es el tiempo en días (desde el 1 de enero, N=1, hasta el 31 de diciembre, N=365), y N1=184 (3 de julio, aphelio) y N2=80 (20 de marzo, equinoccio ascendente).
Dt=Hora solar verdadera - hora solar media:
| > | Dt:=C1*sin(2*Pi*(N-N1)/365)+C2*sin(4*Pi*(N-N2)/365);plot(subs(dat,SI0,Dt/60),N=1..365,Dt_minutes=-15..20);NDtmin:=min[index]([seq(subs(dat,SI0,Dt),N=1..365)]);Dtmin:=evalf(subs(N=%,dat,SI0,Dt/60))*min_;NDtmax:=max[index]([seq(subs(dat,SI0,Dt),N=1..365)]);Dtmax:=evalf(subs(N=%,dat,SI0,Dt/60))*min_; |
 |
|
| (1) |
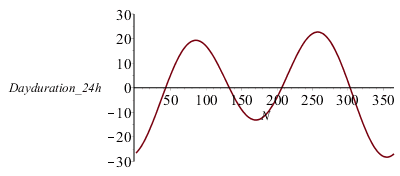
También varía la duración del día a lo largo del año, pero en menos de medio minuto (no como la hora del mediodía, antes calculada, que variaba bastantes minutos).
| > | DDt:=diff(Dt,N);plot(subs(dat,SI0,DDt),N=1..365,Dayduration_24h=-30..30);NDDtmin:=min[index]([seq(subs(dat,SI0,DDt),N=1..365)]);DDtmin:=evalf(subs(N=%,dat,SI0,DDt))*s_;NDDtmax:=max[index]([seq(subs(dat,SI0,DDt),N=1..365)]);DDtmax:=evalf(subs(N=%,dat,SI0,DDt))*s_; |
 |
|
| (2) |
Aparte de esta diferencia de hora solar respecto a un reloj local, habrá que tener en cuenta que desde que se popularizó el ferrocarril ya no se ajustan localmente los relojes, sino por husos horarios, y que, en muchos países se cambia esta hora estándar por una hora oficial que se desvía de su huso, cambia con las estaciones para ahorrar energía, etc.
La hora europea es UTC+1 en invierno y UTC+2 en verano (desde el último domingo de marzo al último domingo de octubre).
| > |