>	restart:#"m13_p18"

Se desea comparar la convección respecto a la radiación en la transmisión de calor de un cuerpo caliente al ambiente (20 ºC). En particular se pide:

a)Para qué valor del coeficiente convectivo serán iguales los flujos de calor convectivos y radiativos en la aproximación lineal (tómese =1).

b) Para qué temperatura del cuerpo caliente serán iguales los flujos de calor convectivos y radiativos si h=10 W/(m2•K).

c) Qué área debe tener un ‘radiador’ para que estando a 65 ºC transmita al aire 1 kW, con h=10 W/(m2•K).

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0):unprotect(Re):

>	dat:=[epsilon=1,h=10*W_/(m_^2*K_),T0=(20+273.15)*K_,Qdot=1e3*W_,Tr=(65+273.15)*K_];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Para qué valor del coeficiente convectivo serán iguales los flujos de calor convectivos y radiativos en la aproximación lineal (tómese =1).

>	Qconv:=h*(T-T0);Qconv_:=h*DT;Qrad:=epsilon*sigma*(T^4-T0^4);Qrad_:=convert(series(subs(T=T0+DT,Qrad),DT=0,2),polynom);heq:=solve(Qconv_=Qrad_,h);heq_:=subs(dat,%);plot(subs(h=heq_,dat,SI0,{Qconv,Qrad}),T=subs(dat,SI0,T0/2..1.5*T0),q=-1000..2000,color=black);

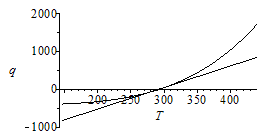i.e. para pequeños DT, son iguales los flujos para h>5.4 W/(m^2.K), y es mayor la convección si h>5.4 W/(m^2.K).

b) Para qué temperatura del cuerpo caliente serán iguales los flujos de calor convectivos y radiativos si h=10 W/(m2•K)..

>	Tcut:=fsolve(subs(dat,SI0,Qrad=Qconv),T);Tcut_:=TKC(%[2]*K_);plot(subs(dat,SI0,{Qconv,Qrad}),T=subs(dat,SI0,T0/2..1.5*T0),q=-1000..2000,color=black);

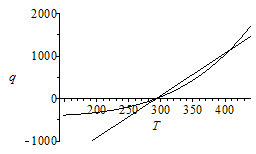i.e. si h=10 W/(m^2.K), es mayor la convección hasta T=134 ºC.

c) Qué área debe tener un ‘radiador’ para que estando a 65 ºC transmita al aire 1 kW, con h=10 W/(m2•K).

Suponiendo placa plana transmitiendo por ambas caras:

>	eqBE:=Qdot=2*A*(h*(Tr-T0)+epsilon*sigma*(Tr^4-T0^4));A_:=subs(dat,solve(%,A));

i.e. ha de tener 0,65 m2 de área frontal (y estar al aire por ambos lados; si estuviese aislado por un lado, haría falta un radiador doble de grande, de 1,3 m2)).

>