p141.html

> restart:#"m13_p14"

Se trata de analizar la influencia de la radiación terresre sobre un radiador circular plano, de 10 cm de diámetro, de un satélite geoestacionario (a 36000 km de altura). Para ello se considera la placa en régimen estacionario recibiendo del satélite un flujo de calor constante que irradia al espacio como cuerpo negro. Sabiendo que la Teq del radiador cuando apunta al espacio vacío es To, se desea calcular el incremento de temperatura cuando apunta hacia la tierra, considerándola a una temperatura media T1 = 288 K, con una emisividad infrarroja eIR = 0,55 y reflectancia solar rs = 0,3. En particular se pide:

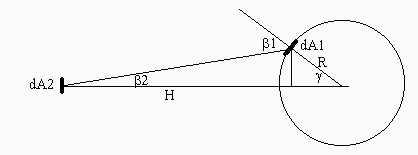
a) Factor geométrico entre la tierra y el radiador.

b) Temperatura del radiador cuando mira a la tierra, despreciando el posible efecto de albedo.

c) Temperatura del radiador cuando mira a la tierra, teniendo en cuenta el máximo valor posible del flujo por albedo.

d) Aplicación para los casos To = 300 K y To = 100 K.

Datos:

> read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(RealDomain):h:='h':phi:='phi':assume(x>0,h>0,phi>=0):

> dat:=[R=6378e3*m_,H=36e6*m_,C[s]=1370*W_/m_^2,R1=0.05*m_,alpha=1,epsilon=1,Tp=288*K_,epsilon2=0.55,albedo=0.3,T01=300*K_,T02=100*K_];

> dat:=op(dat),Const,SI2,SI1:

a) Factor geométrico entre la tierra y el radiador.

Viene tabulado en muchos libros (e.g. ver View factors, y no cuesta mucho deducirlo a partir de su definición): F12=1/1+h)^2.

> eqGEO:=g*(R/(R+H))^2=(2*Pi/Period)^2*(R+H);Period:=86400*s_;eqGEO_:=H=evalf(subs(dat,SI0,solve(eqGEO,H)))*m_;eqh:=h=H/R;eqh_:=subs(dat,eqh);eqVF:=F[12]=1/(1+h)^2;eqVF_:=subs(eqh_,%);

b) Temperatura del radiador cuando mira a la tierra, despreciando el posible efecto de albedo.

La radiación que recibe del planeta es constante si se supone Tp=cte.

> Qp:=alpha*A*F[12]*albedo*C[s];eqA:=A=Pi*R1^2;eqA_:=evalf(subs(dat,%));Qp_:=subs(eqA_,eqVF_,dat,Qp);

i.e. recibe 0,07 W de radiación infrarroja de la Tierra.

c) Temperatura del radiador cuando mira a la tierra, teniendo en cuenta el máximo valor posible del flujo por albedo.

El albedo máximo será en el punto subsolar:

> Qa:=alpha*A*F[12]*epsilon2*sigma*Tp^4;Qa_:=subs(eqA_,eqVF_,dat,Qa);

i.e. recibe 0,04 W de radiación visible reflejada por la Tierra.

d) Aplicación para los casos To = 300 K y To = 100 K.

Si sin recibir nada de la Tierra está a To, está emitiendo Qe=epsilon*sigma*To^4. NOTA. Sólo se toma una cara del radiador que mira a la Tierra.

> Qe:=epsilon*A*sigma*To^4;Qs1:=subs(To=T01,eqA_,dat,Qe);Qs2:=subs(To=T02,eqA_,dat,Qe);

i.e. si el radiador estaba a 300 K (que es lo normal), recibía 3,61 W del satélite, y (0,07+0,04)=1,1 W de la Tierra, lo cual no cambia mucho. Pero si el radiador estaba a 100 K (porque se tratase de una aplicación criogénica), recibía 0,045 W del satélite, y (0,07+0,04)=1,1 W de la Tierra, que ahora son demasiados (la temperatura del radiador subiría de 100 K).