>	restart:#"m13_p13"

Determinar la temperatura de equilibrio de una esfera en el espacio extraterrestre en función de sus propiedades ópticas, suponiendo una irradiación solar Cs=1370 W/m2. En particular se pide:

a)                Determinar la temperatura de equilibrio de una esfera en el espacio extraterrestre.

b) Hacer aplicación para una pintura blanca de / = 0,20/0,85, una pintura negra de /=0,95/0,90, una pintura aluminizada de /= 0,30/0,30 y un papel de oro de /=0,25/0,03.

c)                Hacer aplicación para la Tierra supuesta cuerpo negro.

d) Corregir c) con el efecto del albedo (=0.7).

e) Corregir d) con el efecto de la emisividad (=0.6).

f)                Corregir c) con el efecto de un escudo isotermo negro (cuerpo negro).

g)                Corregir c) con el efecto invernadero ideal.

h)                Corregir c) con el efecto invernadero semitransparente.

i)                 Corregir h) con el efecto de la convección equivalente a h=5 W/(m2.K)

j) Corregir i) para un modelo de Tierra helada con =0,3

k) Corregir i) para un modelo de invierno nuclear con =0,2

l)                 Corregir i) para un modelo de Tierra con sol frío 0,85•Cs.

m) Corregir i) para un modelo de Tierra con sol frío 0,85•Cs pero mucho vapor /0.85

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	dat:=[C[s]=1370*W_/m_^2,a_e[1]=0.2/0.85,a_e[2]=0.3/0.3,a_e[3]=0.25/0.03,alpha=0.67,rho[a]=0.24,rho[t]=0.15,tau[IR]=0.12,h=1*W_/(m_^2*K_),epsilon[a]=0.75,epsilon[t]=0.9,epsilon[IR]=0.6,tau=0.6,HE=0.2];

1=blanca, 2=aluminizada, 3=papel_de_oro, t=tierra, a=aire.

>	dat:=op(dat),Const,SI2,SI1:

a) Determinar la temperatura de equilibrio de una esfera en el espacio extraterrestre.

>	eqBE:=alpha*C[s]*Pi*R^2=4*Pi*R^2*epsilon*sigma*T^4;eqBEdet:=alpha+tau+rho=1;Teq:=sqrt(sqrt(alpha*C[s]/(4*epsilon)));Teq:=solve(subs(epsilon=alpha/a_e,eqBE),T)[1];Teq_:=evalf(subs(dat,SI0,Teq)):'Teq'=evalf(%,3);with(plots):semilogplot({288,Teq_},a_e=1e-1..1e1,T=0..500,color=black);

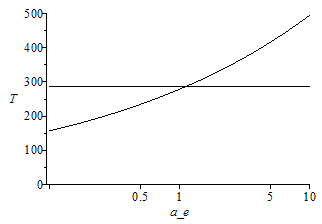b) Hacer aplicación para una pintura blanca de a/e = 0,20/0,85, una pintura negra de a/e = 0,95/0,90, una pintura aluminizada de a/e = 0,30/0,30 y un papel de oro de a/e = 0,25/0,03

>	evalf(subs(dat,[seq(Teq||i=subs(a_e=a_e[i],dat,SI0,Teq)*K_,i=1..3)]));

c) Hacer aplicación para la Tierra supuesta cuerpo negro.

>	Tt0:=subs(a_e=1,Teq);Tt0_:=evalf(subs(dat,SI0,a_e=1,Teq))*K_;

d) Corregir c) con el efecto del albedo (a=0.67).

>	Tt1:=subs(a_e=alpha,Teq);Tt1_:=evalf(subs(a_e=alpha,dat,SI0,Teq))*K_;

e) Corregir d) con el efecto de la emisividad (e=0.6).

>	Tt2:=subs(a_e=alpha/epsilon,Teq);Tt2_:=evalf(subs(a_e=alpha/epsilon [IR],dat,SI0,Teq))*K_;

f) Corregir c) con el efecto de un escudo isotermo negro (cuerpo negro).

Como la Teq del escudo sería la misma, Teq=Teq en c) (y daría atmósfera isoterma).

>	Tt3:='Tt0';

g) Efecto de un invernadero ideal (transparente en el visible y negro en el IR).

eqBE1=balance de flujos por encima del escudo atmosférico.

eqBE2=balance de flujos en la superficie terrestre.

>	eqBE1:=C[s]/4=sigma*Ta^4;eqBE2:=C[s]/4=sigma*(Tt^4-Ta^4);sol1_:=fsolve(subs(dat,SI0,{eqBE1,eqBE2}),{Tt=100..1000,Ta=100..1000}):evalf(allvalues(%))*K_;

h) Corregir g) con el efecto del albedo en el suelo y las emisividades.

>	eqBE1:=C[s]/4=rho[t]*C[s]/4+epsilon[a]*sigma*Ta^4;eqBE2:=(1-rho[t])*C[s]/4=sigma*(Tt^4-Ta^4)/(1/epsilon[a]+1/epsilon[t]-1);sol1_:=fsolve(subs(dat,SI0,{eqBE1,eqBE2}),{Tt=100..1000,Ta=100..1000})*K_;

i) Corregir c) con el efecto invernadero semitransparente.

>	eqBE1:=C[s]/4=rho[a]*C[s]/4+tau*rho[t]*C[s]/4+tau[IR]*epsilon[t]*sigma*Tt^4+epsilon[a]*sigma*Ta^4;eqBE2:=(1-tau-rho[a])*C[s]/4+HE+epsilon[a]*epsilon[t]*sigma*Tt^4-2*epsilon[a]*sigma*Ta^4;sol1_:=fsolve(subs(dat,SI0,{eqBE1,eqBE2}),{Tt=100..1000,Ta=100..1000})*K_;

i) Corregir h) con el efecto de la convección equivalente a h=5 W/(m^2.K).

>	eqBE1:=(1-0.3-0.6*0.4)*C[s]/4=0.6*sigma*Ta^4;eqBE2:=0.6*0.8*C[s]/4=epsilon[IR]*sigma*(Tt^4-Ta^4)+h*(Tt-Ta);sol1_:=fsolve(subs(dat,SI0,{eqBE1,eqBE2}),{Tt=100..1000,Ta=100..1000})*K_;

Estos modelos simples sirven para evaluar sensibilidades a los parámetros, por ejemplo:

j) Tierra helada. El hielo daría alpha_e=0,3 (en vez de 0,9) y la Te pasaría a ser bajo cero, que es consistente.

>	sol1_:=solve(subs(alpha[s]=0.3,dat,{eqBE1/R^2,eqBE2/R^2}),{Tt,Ta})[1];

k) Invierno nuclear. El humo taparía el sol y haría tau=0,2 (en vez de 0,5) y la Te disminuiría.

>	sol1_:=solve(subs(tau=0.2,dat,{eqBE1/R^2,eqBE2/R^2}),{Tt,Ta})[1];

l) Sol frío. Hace unos 2x10^9 años era C=85%Co

>	sol1_:=solve(subs(C[s]=0.85*C[s],dat,{eqBE1/R^2,eqBE2/R^2}),{Tt,Ta})[1];

y sin embargo ya había vida, así que tal vez habría mucho más vapor de agua y se compensara.

m) Sol frío. Si C=85%Co y alpha=alphao/85%:

>	sol1_:=solve(subs(alpha[s]=alpha[s]/0.85,C[s]=0.85*C[s],dat,{eqBE1/R^2,eqBE2/R^2}),{Tt,Ta})[1];

>