>	restart:#"m13_p11"

Calcular la distribución de temperatura en una cáscara esférica en el espacio interestelar, sometida a la radiación solar y suponiendo el interior adiabático. Los datos son: la irradiación solar E [W/m2], la absortancia solar , la emisividad infrarroja , la conductividad térmica k, el espesor de la cáscara  y el radio de la esfera R. En particular, se pide:

a) La temperatura en el límite k.

b)                 La ley de temperaturas para k=0.

c) El perfil de temperaturas para k=10 W/(mK), E=1370 W/m2•K), R=0,1 m, =1 mm, =1 y =1.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0):unprotect(Re):with(plots):

>	su:="Aluminio_pulido":dat:=[k=10*W_/(m_*K_),E=1370*W_/m_^2,R=0.1*m_,d=0.001*m_,alpha=1,epsilon=1];

>	sdat:=get_sol_data(su):dat:=op(dat),Const,SI2,SI1:

a) La temperatura en el límite k>>.

Si la conductividad es muy grande no puede haber gradientes térmicos, luego será isotermo.

>	eqBE:=alpha*E*Pi*R^2=4*Pi*R^2*epsilon*sigma*T^4;Tst:=solve(eqBE,T)[1];Tst_:=evalf(subs(dat,SI0,Tst))*K_;

b) Tmáx para k=0.

Si no hay conducción en la cáscara, cada elemento tendrá su temperatura estacionaria local. Habrá simetría axial.

Sea beta el ángulo con la dirección subsolar. El factor de visión será:

>	f:=proc(beta) RETURN(piecewise(beta<Pi/2,cos(beta),0)) end:plot(f(beta),beta=0..Pi,F=0..1,axes=boxed);

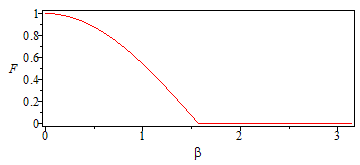y del balance energético local se obtiene:

>	eqBE2:=alpha*E*f(beta)=epsilon*sigma*T^4;Tk0:=solve(eqBE2,T)[1];pl12:=plot(subs(dat,SI0,{Tst_,Tk0}),beta=0..Pi,T=0..400);Tmax:=evalf(subs(dat,(alpha*E/(epsilon*sigma))^(1/4))):display(pl12);

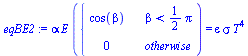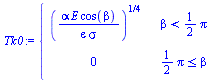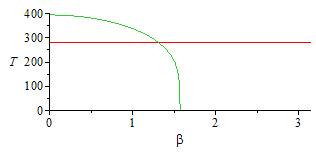Se ha dibujado las dos soluciones anteriores. Nótese que, sin conducción, la cara no iluminada quedaría en equilibrio con la radiación de fondo cósmica, a 2,7 K.

c)  El perfil de temperaturas para k=10 W/(mK), E=1370 W/m2•K), R=0,1 m, =1 mm, =1 y =1.

El balance energético de una tira circular en posición beta y de anchura R*dbeta, será:

>	eqBE3:=0=2*Pi*R*sin(beta)*d*k*Laplacian(T(beta))+2*Pi*R*sin(beta)*R*alpha*E*cos(beta)*f(beta)-2*Pi*R*sin(beta)*R*epsilon*sigma*T(beta)^4;eqBE3:=0=d*k*(diff(sin(beta)*diff(T(beta),beta),beta))/(R^2*sin(beta))+alpha*E*cos(beta)*f(beta)-epsilon*sigma*T(beta)^4;

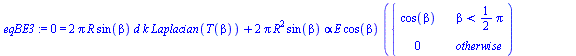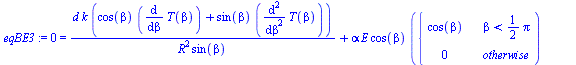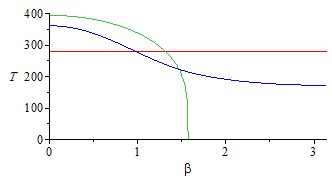
Es una equación diferencial ordinaria de 2º grado con condiciones de contorno dT/dbeta=0 en beta=0 y en beta=Pi, que se integraría por condiciones iniciales T(0)=T0 y D(T)(0)=0 e iterando en T0 hasta ebcontrar D(T)(Pi)=0. Pero es muy sensible a las condiciones iniciales, así que hay que proceder con mucha cautela.

>	To:=361.2;T_:=dsolve(subs(dat,SI0,{eqBE3,D(T)(0)=0,T(0)=To}),type=numeric);pl3:=odeplot(T_,beta=1e-2..Pi-1e-2,view=[0..Pi,0..400],color=blue):display([pl12,pl3]);

Podemos ver también la derivada, dT/dbeta, o mejor el flujo de calor a través de la sección de cáscara, en [W], que sería Q(beta)=k*2*Pi*R*sin(beta)*d*dT/dbeta.

>	Qbeta:=-k*2*Pi*R*sin(beta)*d*diff(T(beta),beta);odeplot(T_,subs(dat,SI0,[beta,Qbeta]),beta=1e-2..Pi-1e-2,view=[0..Pi,0..1]);

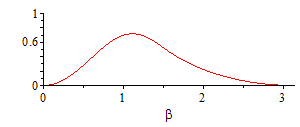i.e. el flujo de calor es máximo a unos 60º de ángulo zenital.

>