>	restart:#"m13_p08"

Se quiere estimar la temperatura del sol por los dos procedimientos siguientes:

a) Sabiendo que la temperatura media de la tierra es 15 °C, que su radio es de 6378 km, que el ángulo del disco solar es 0,01 rad y que la distancia al sol es de 0,15.1012 m, detallando las simplificaciones introducidas y calcular también la constante de radiación solar (irradiación a una unidad astronómica).

b) Sabiendo que la luz solar presenta su máxima intensidad espectral para l=0,5.10 6 m.

c) Calcular con lo anterior la temperatura de equilibrio de una esfera en función de su distancia al sol.

d) Sabiendo que el sol se ve desde la tierra con un ángulo de 0,01 rad, que la irradiancia máxima en superficie es de 1000 W/m2, y que se estiman en un 30% las pérdidas por absorción en la atmósfera.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	dat:=[T0=(273+15)*K_,R=6378e3*m_,beta=0.01,L=0.15e12*m_,lambda[m]=0.5e-6*m_,E=1000*W_/m_^2,a=0.3];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Sabiendo que la temperatura media de la tierra es 15 °C, que su radio es de 6378 km, que el ángulo del disco solar es 0,01 rad y que la distancia al sol es de 0,15.1012 m, detallando las simplificaciones introducidas y calcular también la constante de radiación solar (irradiación a una unidad astronómica).

(Nota histórica. Fue Cassini en 1673 el primero en calcular con precisión la distancia al Sol, por triangulación con la posición de Marte. Y fue Stefan en 1880 el primero en dar una estimación de la temperatura del Sol, a partir de experimentos realizados por Soret en los que medía que la irradiancia solar era unas 29 veces mayor que la de una placa al rojo vivo, que Stefan supuso a unos 2200 K.)

>

eq1:=sigma*T[s]^4*4*Pi*R[s]^2/(4*Pi*L^2)*Pi*R^2=4*Pi*R^2*sigma*T^4;;eq2:=C[s]=sigma*T[s]^4*4*Pi*R[s]^2/(4*Pi*L^2);eq3:=C[s]*Pi*R^2=4*Pi*R^2*sigma*T^4;eq4:=beta=2*R[s]/L;eq3_:=C[s]=evalf(subs(T=T0,dat,solve(eq3,C[s])));sol1:=solve({eq1,eq4},{R[s],T[s]});R[s_]:=subs(sol1,dat,R[s]);T[s_]:=allvalues(subs(sol1,T=T0,dat,T[s]))[1];

i.e. con los datos del enunciado, la constante solar sería Cs=1560 W/m2 en lugar de los 1370 W/m2 reales, y la temperatura del Sol sería de 5760 K, que es la verdadera.

b) Sabiendo que la luz solar presenta su máxima intensidad espectral para l=0,5.10 6 m

>	eq5:=lambda[m]*T=C[W];eq5_:=T[s]=subs(dat,C[W]/lambda[m]);

i.e. se obtiene casi lo mismo; los 5800 K de la fotosfera del Sol.

c) Calcular con lo anterior la temperatura de equilibrio de una esfera en función de su distancia al sol.

>

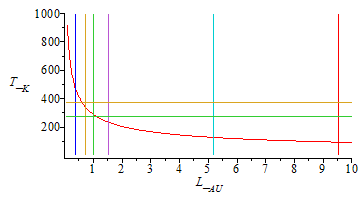
AU_:=subs(dat,L);Teq:=T[s]*sqrt(R[s]/(2*L));Llist:=[[58/150,1],[58/150+1e-3,1000]],[[108/150,1],[108/150+1e-3,1000]],[[150/150,1],[150/150+1e-3,1000]],[[228/150,1],[228/150+1e-3,1000]],[[778/150,1],[778/150+1e-3,1000]],[[1427/150,1],[1427/150+1e-3,1000]]:with(plots):plot({[[1e-6,273],[10,273]],[[1e-6,373],[10,373]],Llist,subs(L=L_[AU]*AU_,R[s]=R[s_],eq5_,SI0,Teq)},L_[AU]=0.1..10,'T_[K]'=0.1..1000);semilogplot({[[1e-6,273],[10,273]],[[1e-6,373],[10,373]],Llist,subs(L=L_[AU]*AU_,R[s]=R[s_],eq5_,SI0,Teq)},L_[AU]=0.1..10,'T_[K]'=0.1..1000);

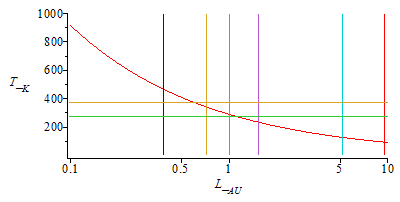Para las posiciones de Mercurio (0,39 AU), Venus, La Tierra, Marte, Júpiter y Saturno (9,5 AU), las temperaturas de cuerpo negro serían:

>	T__:=evalf(subs(L=L_[AU]*AU_,R[s]=R[s_],eq5_,SI0,Teq));L__:=evalf(seq(op(1,op(1,op(i,[Llist]))),i=1..nops([Llist]))):T___:=evalf(seq(subs(L_[AU]=L__[i],T__),i=1..nops([L__]))):evalf(seq([L__[i]*AU,T___[i]*K],i=1..nops([L__])));

En realidad los planetas y sus lunas no son cuerpos negros, y sus temperaturas superficiales cambian (e.g. la temperatura media de la superficie Venus es 730 K y no 342 K).

d) Sabiendo que el sol se ve desde la tierra con un ángulo de 0,01 rad, que la irradiancia máxima en superficie es de 1000 W/m2, y que se estiman en un 30% las pérdidas por absorción en la atmósfera.

La conservación de la energía solar desde que se emite en el radio del sol, Rs, hasta que llega a la tierra, Rsp, es:

>	eqBE:=4*Pi*Rs^2*sigma*Ts^4=C[s]*4*Pi*Rsp^2;eqdat1:=2*Rs/Rsp=beta;eqdat2:=C[s]*(1-a)=E;Ts:=(E/((1-a)*sigma*(beta/2)^2))^(1/4);Ts_:=evalf(subs(dat,%));