>	restart:#"m13_p02"

Para cuerpos negros a diferentes temperaturas, T1=5800 K (sol), T2=2900 K (filamento de wolframio), T3=1000 K (hierro al rojo) y T4=300 K (tierra), calcular:

a) La longitud de onda de máxima emisión.

b) La fracción de energía radiante emitida entre 0,4 µm y 0,7 µm (rango visible).

c) La emitancia.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):

>	dat:=[T1=5800*K_,T2=2900*K_,T3=1000*K_,T4=300*K_,l1=0.3e-6*m_,l2=0.4e-6*m_,l3=0.7e-6*m_,l4=3e-6*m_,l5=3e-3*m_];

Eqs. const.:

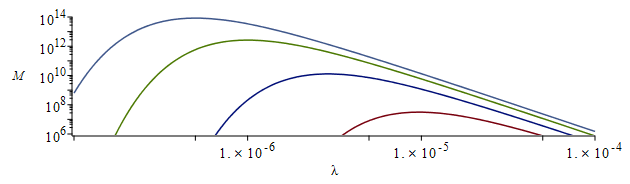
>	dat:=op(dat),Const,SI2,SI1:eq13_1;loglogplot([seq(subs(A=A[P],B=B[P],dat,SI0,rhs(eq13_1)),T in [300,1000,2900,5800])],lambda=1e-7..1e-4,'M'=1e6..1e14);

a) Calcular la longitud de onda de máxima emisión.

Aplicando la ley de Wien.

>	eq13_3;eq2:=lambda*T=C[W]:for i from 1 to 4 do eq2_:=lambda=subs(T=cat(T,i),dat,solve(eq2,lambda));print(`T=`,subs(dat,T||i),eq2_,`Mmax=`,evalf(subs(A=A[P],B=B[P],T=subs(dat,T||i),eq2_,dat,SI0,rhs(eq13_1))));od:

i.e. la máxima emisión a 5800 K es a 0,5 micrómetros, a 3000 K 1 micrómetro a 1000 K 3 micrómetros, y a 300 K 10 micrómetros.

Nótese que la emitancia espectral máxima es proporcional a T^5, siendo la constante de proporcionalidad K=12.9·10^-6 W/(m·K^5), i.e. Mm=K*T^5; e.g. a T=1000 K, Mm=12.9·10^9 W/m.

>	M[lambda,max]:=subs(lambda=C[W]/T,rhs(eq13_1));M[lambda,max_]:=K*T^5;K:=evalf(subs(A=A[P],B=B[P],dat,SI0,M[lambda,max]/T^5))*1e6*W_/(m_^2*micrometre_*K_^5);

b) La fracción de energía radiante emitida entre 0,4 µm y 0,7 µm (rango visible).

Integrando la ley de Planck.

>

eq13_1;eq3:=Frac=Int(rhs(eq13_1),lambda=l1..l2)/rhs(eq13_2);for i from 1 to 4 do FracUV||i:=evalf(subs(T=cat(T,i),A=A[P],B=B[P],dat,SI0,rhs(eq3)));FracVIS||i:=evalf(subs(l2=l3,l1=l2,T=cat(T,i),A=A[P],B=B[P],dat,SI0,rhs(eq3)));FracIRc||i:=evalf(subs(l2=l4,l1=l3,T=cat(T,i),A=A[P],B=B[P],dat,SI0,rhs(eq3)));FracIRl||i:=evalf(subs(l2=l5,l1=l4,T=cat(T,i),A=A[P],B=B[P],dat,SI0,rhs(eq3)));od;

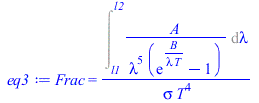i.e. a 5800 K se emite el 9% en el UV, el 37% en el rango visible (aunque el ojo humano capta menos porque hay que multiplicar for el filtro de visión), un 49% en el IR cercano (hasta 3 micrómetros), y un 2% en el IR lejano.

A 2900 K se emite el 0,1% en el UV, el 7% en el rango visible (aunque el ojo humano capta menos porque hay que multiplicar for el filtro de visión), un 81% en el IR cercano (hasta 3 micrómetros), y un 12% en el IR lejano.

A 1000 K ya sólo se emite IR, un 27% en el IR cercano (hasta 3 micrómetros), y un 73% en el IR lejano.

A 300 K ya todo se emite en el IR lejano.

Pero, en lugar de integrar numéricamente, suele ser más útil el desarrollo en serie:

>	Frac:=(15/Pi^4)*Sum((x^3+3*x^2+6*x+6)*exp(-x)/n^4,n=1..N);x:=n*B[P]/(lambda*T);Frac_:=value(subs(N=9,Frac)):Check5800:=1=evalf(subs(T=T1,lambda=999e-6,dat,SI0,Frac_));Check300:=1=evalf(subs(T=T4,lambda=999e-6,dat,SI0,Frac_));

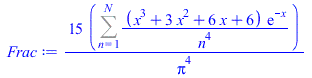En el UV:

>

FracUV1:=evalf(subs(T=T1,lambda=subs(dat,l2),dat,Frac_)-subs(T=T1,lambda=subs(dat,l1),dat,Frac_));FracUV2:=evalf(subs(T=T2,lambda=subs(dat,l2),dat,Frac_)-subs(T=T2,lambda=subs(dat,l1),dat,Frac_));FracUV3:=evalf(subs(T=T3,lambda=subs(dat,l2),dat,Frac_)-subs(T=T3,lambda=subs(dat,l1),dat,Frac_));FracUV4:=evalf(subs(T=T4,lambda=subs(dat,l2),dat,Frac_)-subs(T=T4,lambda=subs(dat,l1),dat,Frac_));

En el visible:

>

FracVIS1:=evalf(subs(T=T1,lambda=subs(dat,l3),dat,Frac_)-subs(T=T1,lambda=subs(dat,l2),dat,Frac_));FracVIS2:=evalf(subs(T=T2,lambda=subs(dat,l3),dat,Frac_)-subs(T=T2,lambda=subs(dat,l2),dat,Frac_));FracVIS3:=evalf(subs(T=T3,lambda=subs(dat,l3),dat,Frac_)-subs(T=T3,lambda=subs(dat,l2),dat,Frac_));FracVIS4:=evalf(subs(T=T4,lambda=subs(dat,l3),dat,Frac_)-subs(T=T4,lambda=subs(dat,l2),dat,Frac_));

En el IR cercano:

>

FracIRc1:=evalf(subs(T=T1,lambda=subs(dat,l4),dat,Frac_)-subs(T=T1,lambda=subs(dat,l3),dat,Frac_));FracIRc2:=evalf(subs(T=T2,lambda=subs(dat,l4),dat,Frac_)-subs(T=T2,lambda=subs(dat,l3),dat,Frac_));FracIRc3:=evalf(subs(T=T3,lambda=subs(dat,l4),dat,Frac_)-subs(T=T3,lambda=subs(dat,l3),dat,Frac_));FracIRc4:=evalf(subs(T=T4,lambda=subs(dat,l4),dat,Frac_)-subs(T=T4,lambda=subs(dat,l3),dat,Frac_));

En el IR lejano:

>

FracIRl1:=evalf(subs(T=T1,lambda=subs(dat,l5),dat,Frac_)-subs(T=T1,lambda=subs(dat,l4),dat,Frac_));FracIRl2:=evalf(subs(T=T2,lambda=subs(dat,l5),dat,Frac_)-subs(T=T2,lambda=subs(dat,l4),dat,Frac_));FracIRl3:=evalf(subs(T=T3,lambda=subs(dat,l5),dat,Frac_)-subs(T=T3,lambda=subs(dat,l4),dat,Frac_));FracIRl4:=evalf(subs(T=T4,lambda=subs(dat,l5),dat,Frac_)-subs(T=T4,lambda=subs(dat,l4),dat,Frac_));

Es interesante ver cómo varía la fracción visible del total de radiación del cuerpo negro:

>	plot(subs(SI0,evalf(subs(T=T_K,lambda=subs(dat,l3),dat,Frac_)-subs(T=T_K,lambda=subs(dat,l2),dat,Frac_))),T_K=0..10000,VIS_fract=0..0.5);

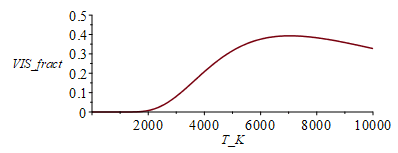i.e. la fracción en el rango visible (0,4..0,7 micrómetros) es máxima con VIS_fract=0,40 a unos 7000 K, aunque la energía visible por el ojo humano sería algo menor por la curva de visión estándar).

c) La emitancia.

Integrando la ley de Stefan-Boltzmann:

>	eq13_2;for i from 1 to 4 do M||i:=evalf(subs(T=cat(T,i),dat,rhs(eq13_2)));od;

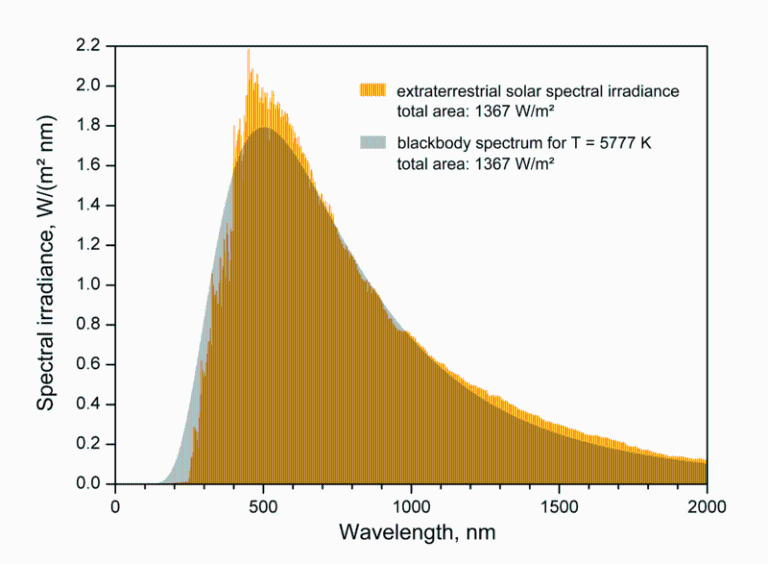
i.e. una superficie a 5800 K emite 64 MW/m2, a 3000 K 4 MW/m2, a 1000 K 57 kW/m2, y a 1000 K 0,5 kW/m2. La irradiancia solar media extraterrestre es 1370 W/m2, que corresponde a una atenuación esférica desde Rsol=0,7e9 m hasta Rsol_tierra=150e9 m, i.e. E=Msol(Rsol/Rsol_tierra)^2=64e6*(0,7/150)^2=1370 W/m2.

Respecto a la emitancia espectral, la ley de Planck enseña que, para una misma longitud de onda, M aumenta con la temperatura, como se puede apreciar en la Fig. 1; e.g. un cuerpo negro a 5800 K, como el Sol, emite a lambda=10 micrómetros más potencia que un cuerpo negro a 300 K (13 W/(m^2·nm) frente a 0,031 W/(m^2·nm)). Pero lo que suele compararse no son emitancias sino la irradiancia solar con la emitancia terrestre, y entonces sí es Esol=Msol*(Rsol/Rsol_tierra)^2=13*(0,7/150)^2=0,0003 W/(m^2·nm) es menor que Mtierra=0,031 W/(m^2·nm). Análogamente, no suele hablarse de la emitancia espectral solar máxima, que es de 84 kW/(m^2·nm) como se ve en la Fig. 1, sino de la irradiancia espectral solar máxima, que es de 84000*(0,7/150)^2=1,8 W/(m^2·nm). Realmente estos valores corresponden al ajuste de la radiación solar como cuerpo negro a 5800 K; la real se desvía un poco y tiene un valor ligeramente superior a 2 W/(m^2·nm), como se muestra en la figura.

>

>