>	restart:#"m11_p12"

Un aceite de viscosidad 40•10-6 m2/s circula por un tubo de 1 cm de diámetro, recibiendo 100 W/m de potencia térmica por unidad de longitud. Sabiendo que el flujo másico es de 0,02 kg/s, se pide:
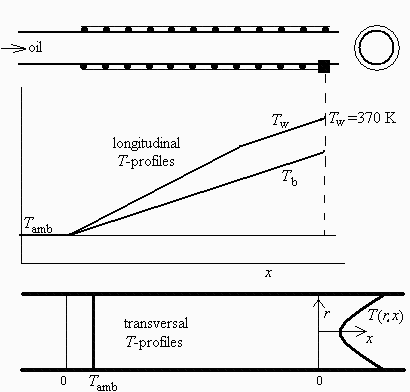
a) Esquematizar el perfil de temperatura esperado a lo largo y ancho del tubo.
b) Determinar el perfil transversal de temperatura y la media másica, cuando la temperatura en la pared alcanza 370 K.
c) Coeficiente convectivo, gradiente térmico en la pared y número de Nusselt, en el caso anterior.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="Aceite":dat:=[mu=40e-3*Pa_*s_,D=0.01*m_,Q_L=100*W_/m_,mdot=0.02*kg_/s_,Tw=370*K_];

Esquema:

Eqs. const.:

>	dat:=op(dat),get_liq_data(su),Const,SI2,SI1:nu_:=subs(dat,mu/rho);a_:=subs(dat,k/(rho*c));

a) Esquematizar el perfil de temperatura esperado a lo largo y ancho del tubo.

(Ver figura.)
b) Determinar el perfil transversal de temperatura y la media másica.

Hay que determinar el tipo de flujo.

>	eqm:=m=rho*u*A;eqAb:=A=Pi*D^2/4;eqAw:=A=Pi*D*L;um_:=evalf(subs(m=mdot,eqAb,dat,solve(eqm,u)));eq12_30:=Rey=u*D/nu;eq12_4:=Pr=nu/a;eqRe_:=subs(nu=nu_,u=um_,dat,eq12_30);eqPr_:=subs(a=a_,nu=nu_,dat,eq12_4);eq12_62_1;L[e,th]=subs(eqRe_,eqPr_,dat,rhs(%)*D);

i.e. el régimen es claramente laminar, pero hasta unos 17 m desde la entrada al tubo no se alcanzará el perfil térmico completamente desarrollado.

Suponiendo régimen laminar desarrollado:

>

equ:=u(r)=2*u[m]*(1-r^2/R^2);eqT:=eq12_67;eqq:=eq12_67_3;eqq1:=qdot=Q/(Pi*D*L);eqq1_:=qdot=evalf(subs(dat,Q_L/(Pi*D)));eqq2:=qdot=rhs(eqq);eqTp:=dT_dx=solve(%,Tprime);eqTp_:=subs(u[m]=um_,eqq1_,c[p]=c,R=D/2,dat,%);eq12_67_2;'Tw'=TKC(subs(dat,Tw));eqTb:=Tb=subs(Tw(x)=Tw,Tprime=rhs(eqTp_),R=D/2,a=a_,u[m]=um_,dat,solve(eq12_67_2,Tb(x)));'Tb'=TKC(rhs(%));eqT_:=subs(Tw(x)=Tw,Tb(x)=Tb,eqTb,Tprime=rhs(eqTp_),u[m]=um_,a=a_,R=D/2,dat,eqT);eqTr0:=subs(r=0,%);'T[0]'=TKC(rhs(%));plot([subs(SI0,rhs(eqT_))-273,r,r=-0.005..0.005],0..100);

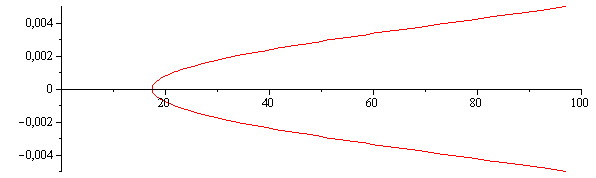i.e., el aceite, cuando en la pared alcanza 370 K, en el eje tan sólo tiene 290 K, y la media másica es de 321 K.

Nótese que si su Tb=48 ºC y su dT/dx=2,5 ºC/m, al ser Lentrada=17 m el aceite hubo de entrar por debajo de 48-2,5*17=5,5 ºC.

c) Coeficiente convectivo, gradiente térmico en la pared, y número de Nusselt.

No confundir con el gradiente térmico longitudinal, que se ha visto que es Tprime=2,5 K/m.

>	eqh:=qdot=h*(Tw-Tb);h_:=subs(eqq1_,eqTb,dat,solve(%,h));eqq:=qdot=k*Diff(T,r)[r=R];dT_drR:=qdot/k;dT_drR_:=subs(eqq1_,dat,%);eqNu:=subs(L=D,eq12_2);eqNu_:=subs(h=h_,dat,%);

>