>	restart:#"m12_p10"

Se quiere enfriar un flujo de 0,8 kg/s de queroseno desde 90 ºC hasta 60 ºC, en un cambiador de calor a contracorriente con agua a 10 ºC. Suponiendo un coeficiente global de transmisión de calor de 300 W/(m2•K), se pide:
a) Caudal mínimo necesario de agua.
b) Caudal necesario de agua suponiendo que la eficiencia del cambiador va a ser del 50%.
c) Área de intercambio necesaria.
d) Número de unidades de transferencia.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Queroseno":su2:="H2O":dat:=[mc=0.8*kg_/s_,Tce=(90+273.15)*K_,Tcs=(60+273.15)*K_,Tfe=(10+273.15)*K_,K=300*W_/(m_^2*K_),eta=0.5];

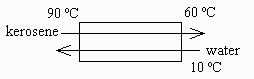
Esquema:

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:Cdat:=get_liq_data(su1):Fdat:=get_liq_data(su2):c=subs(Cdat,c);eq12_7:=mu[water](T)=0.0011*Pa_*s_*exp(-5.6*(1-288*K_/T));#nu_:=subs(dat,mu/rho);a_:=subs(dat,k/(rho*c))

a) Caudal mínimo necesario de agua.

El agua nunca podría llegar a la TCe=90 ºC.

>	eqTfs_max:=Tfs=Tce;eqTfs_max_:=subs(dat,%);Tfs=TKC(rhs(%));eqQ:=Q=mc*cc*(Tce-Tcs);eqQ_:=subs(cc=c,Cdat,dat,%);eqBEf:=Q=mf*cf*(Tfs-Tfe);mf_min_:=subs(cf=c,Fdat,eqTfs_max,eqQ_,dat,solve(%,mf));

i.e., como mínimo habrá que bombear 0,14 kg/s de agua.

b) Caudal necesario de agua suponiendo que la eficiencia del cambiador va a ser del 50%.

>	eq12_96:=eta=Q/Q[max];eq_mc:=(mc*cc>mf*cf);eq_mc_:=(subs(Cdat,dat,mc*c)>subs(Fdat,mf_min_*c));eqeta_:=eta=(Tfs-Tfe)/(Tce-Tfe);Tfs_:=subs(dat,solve(%,Tfs));Tfs=TKC(%);eqBEf:=Q=mf*cf*(Tfs-Tfe);mf_:=subs(cf=c,Fdat,Tfs=Tfs_,eqQ_,dat,solve(%,mf));eq_mc_:=(subs(Cdat,dat,mc*c)>subs(Fdat,mf_*c));

i.e. serán necesarios el doble de agua (0,287 kg/s en vez de 0,144 kg/s). Nótese que se ha vuelto a comprobar que el flujo con menor capacidad térmica global es el frío, para pasar de eq12_96 a eqeta_.

c) Área de intercambio necesaria.

>	eqBEfc:=Q=K*A*DTfc;DTfc_AMTD:=((Tce-Tfs)+(Tcs-Tfe))/2;DTfc_AMTD_:=subs(Tfs=Tfs_,dat,%);DTfc_LMTD:=((Tce-Tfs)-(Tcs-Tfe))/ln((Tce-Tfs)/(Tcs-Tfe));DTfc_LMTD_:=evalf(subs(Tfs=Tfs_,dat,%));eqA:=A=solve(eqBEfc,A);eqA_:=subs(eqQ_,DTfc=DTfc_LMTD_,dat,%);

i.e. hacen falta 3,57 m2 de superficie de intercambio.

d) Número de unidades de transferencia.

>	eq12_97:=N=K*A/(m*c)[min];eqN:=subs(eqA_,Fdat,dat,K*A/(mf_*c));eq12_95:=c=(m*c)[min]/(m*c)[max];eqc:=c=subs(cf=c,Fdat,cc=c,Cdat,dat,(mf_*cf)/(mc*cc));eq12_98:=N=ln((1-c*eta)/(1-eta))/(1-c);eqN_:=evalf(subs(eqc,dat,%));

i.e. hemos comprobado que la definición y la función N(eta,c) dan lo mismo: N=0.9 unidades de transferencia.

>