| > | restart:#"m12_p07" |
Una delgada placa metálica, plana, de 1,5•0.3 m2, se encuentra en presencia de una corriente de aire a 11 m/s paralela a uno de sus lados. La placa lleva unas resistencias eléctricas embebidas que disipan 1 kW en total. Se pide, para las dos posiciones posibles de la placa (a lo largo y a lo ancho):
a) Determinar el tipo de flujo que tendrá lugar, hacer un esquema de la capa límite, y determinar el espesor máximo.
b) Calcular la temperatura que alcanza la placa, suponiéndola isoterma y con el coeficiente convectivo calculado con la correlación de Colburn-Chilton.
c) Indicar la influencia que tendría el hecho de que la conductividad térmica de la placa no fuese muy grande.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su:="Aire":dat:=[L1=1.5*m_,L2=0.3*m_,Q=1e3*W_,u[infinity]=11*m_/s_]; |
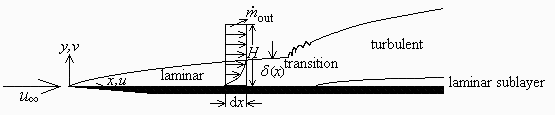
Esquema:
Eqs. const.:
| > | dat:=op(dat),get_gas_data(su),Const,SI2,SI1:nu_:=subs(dat,mu*R*T0/p0);a_:=subs(dat,k*R*T0/(c[p]*p0)); |
a) Determinar el tipo de flujo que tendrá lugar, hacer un esquema de la capa límite, y determinar el espesor máximo.
Depende del nº de Reynolds.
Se desprecia el efecto de los bordes laterales.
Si sopla a lo largo:
| > | eq12_3:=Rey=u*L/nu;eqRe1:=subs(u=u[infinity],nu=nu_,L=L1,dat,%);eq12_29:=Rey[tr]=0.5e6;xt:=Rey[tr]*nu/u[infinity];xt_:=subs(eq12_29,nu=nu_,dat,%);eq12_4_1:=nu=mu/rho;eq12_4:=Pr=nu/a;eqPr:=subs(nu=nu_,a=a_,%); |
El Reynolds local al final de la placa es mayor que el de transición, luego hay transición de laminar a turbulenta, que supondremos tiene lugar bruscamente a una longitud xt=0,75 m.
| > | eq12_21_1:=delta=4.92*sqrt(x*nu/u[infinity]):eqd_lam:=eq12_21_1;eqd_tran:=evalf(subs(x=xt_,nu=nu_,dat,%));eq12_32:=delta/x=0.38/Rey[x]^(1/5);eqd_turb:=subs(Rey[x]=u[infinity]*x/nu,%*x);eqdL:=subs(x=L1-xt,eq12_29,eqd_turb):eqdL_:=evalf(subs(nu=nu_,dat,%));plot(subs(nu=nu_,dat,SI0,[rhs(eqd_lam),subs(x=x-xt_,rhs(eqd_turb))]),x=0..1.5,d=0..0.1); |
![delta = `+`(`/`(`*`(.38, `*`(x)), `*`(`^`(`/`(`*`(u[infinity], `*`(x)), `*`(nu)), `/`(1, 5)))))](images/p07_16.gif) |
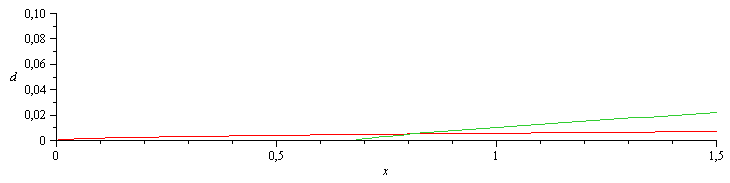 |
i.e. acaba con 22 mm de espesor..
Si sopla a lo ancho:
| > | eq12_3:=Rey=u*L/nu;eqRe2:=subs(u=u[infinity],nu=nu_,L=L2,dat,%);eqdL:=subs(x=L2,eqd_lam);eqdL_:=evalf(subs(nu=nu_,dat,%));plot(subs(nu=nu_,dat,SI0,rhs(eqd_lam)),x=0..0.3,d=0..0.1); |
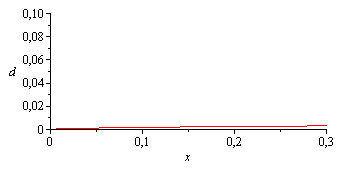 |
i.e. acaba con 3 mm de espesor..
b) Calcular la temperatura que alcanza la placa, suponiéndola isoterma y con el coeficiente convectivo calculado con la correlación de Colburn-Chilton.
Consideramos que están expuestas ambas caras.
Antes de empezar con correlaciones empíricas, veamos lo que daría con un coeficiente convectivo típico, h=50 W/(m2·K) para convección forzada en aire.
| > | eqh:=h=50*W_/(m_^2*K_);eqBE:=Q=h*A*DT;DT:=Q/(h*2*L1*L2);DT_:=subs(eqh,dat,%); |
i.e. la placa quedaría a 22 ºC más que el aire.
Con la correlación de Colburn-Chilton.
Si sopla a lo largo, se usa la correlación turbulenta, que incluye la parte laminar:
| > | eq12_42:=Nus[L]=(0.037*Rey[L]^0.8-870)*Pr^(1/3);eqNu1:=subs(Rey[L]=Rey,eqRe1,eqPr,%);eq12_2:=Nus=h*L/k;eqh1_:=h=subs(L=L1,dat,subs(Nus=Nus[L],eqNu1,solve(eq12_2,h)));'DT'=DT;DT1_:=subs(eqh1_,dat,DT); |
i.e., no era buena la suposición anterior, de h=50 W/(m2·K), y en realidad la placa quedaría con 46 ºC más que el aire (no 22 ºC).
Si sopla a lo ancho, se usa la de laminar:
| > | eq12_27:=Nus[L]=0.66*Pr^(1/3)*Rey[L]^(1/2)*(1-(x[0]/L)^(3/4))/(1-x[0]/L):eqNu:=subs(x[0]=0,eq12_27);eqNu2:=subs(Rey[L]=Rey,eqRe2,eqPr,%);eqh2_:=h=subs(L=L2,dat,subs(Nus=Nus[L],eqNu2,solve(eq12_2,h)));DT1_:=subs(eqh2_,dat,DT); |
i.e. 49 ºC más que el aire, si sopla de través (no los 22 ºC previamente calculados). Se comprueba que es algo más efectivo el enfriamiento cuando sopla a lo largo.
c) Indicar la influencia que tendría el hecho de que la conductividad térmica de la placa no fuese muy grande.
La T(x,y) dependería de la distribución de la energía disipada, q(x,y), de la cercanía al borde de entrada (x ó y) y de la cercanía a los bordes (que no contabilizamos).
Si sopla a lo largo, habrá una transición:
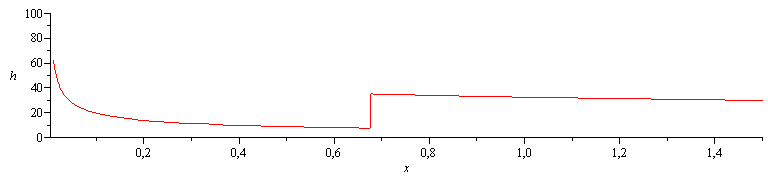
| > | eq12_26:=Nus[x]=0.33*Pr^(1/3)*Rey[x]^(1/2)*(1-(x[0]/x)^(3/4))^(-1/3):eqh1lam:=h=subs(x[0]=0,Rey[x]=u[infinity]*x/nu,rhs(eq12_26)*k/x);eqh1lam_:=evalf(subs(eqPr,nu=nu_,dat,%));eq12_41:=Nus[x]=0.03*Pr^(1/3)*Rey[x]^(4/5);eqh1turb:=h=subs(Rey[x]=u[infinity]*x/nu,rhs(eq12_41)*k/x);eqh1turb_:=evalf(subs(eq12_29,eqPr,nu=nu_,dat,%));h1_:=piecewise(x<xt_,rhs(eqh1lam_),rhs(eqh1turb_));plot(evalf(subs(SI0,h1_)),x=1e-2..1.5,h=0..100); |
![`:=`(eqh1lam, h = `+`(`/`(`*`(.33, `*`(`^`(Pr, `/`(1, 3)), `*`(sqrt(`/`(`*`(u[infinity], `*`(x)), `*`(nu))), `*`(k)))), `*`(x))))](images/p07_38.gif) |
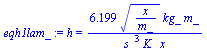 |
![`:=`(eqh1turb, h = `+`(`/`(`*`(0.3e-1, `*`(`^`(Pr, `/`(1, 3)), `*`(`^`(`/`(`*`(u[infinity], `*`(x)), `*`(nu)), `/`(4, 5)), `*`(k)))), `*`(x))))](images/p07_41.gif) |
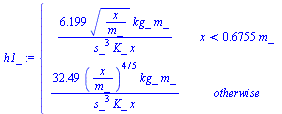 |
 |
Si sopla a lo ancho:
| > | eqh1lam:=h=subs(x[0]=0,Rey[x]=u[infinity]*x/nu,rhs(eq12_26)*k/x);h2_:=evalf(subs(eqPr,nu=nu_,dat,rhs(%)));plot(evalf(subs(SI0,h2_)),x=0..0.3,h=0..100); |
![h = `+`(`/`(`*`(.33, `*`(`^`(Pr, `/`(1, 3)), `*`(`^`(`/`(`*`(u[infinity], `*`(x)), `*`(nu)), `/`(1, 2)), `*`(k)))), `*`(x)))](images/p07_45.gif) |
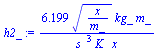 |
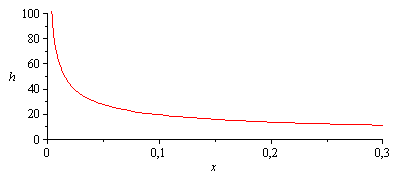 |
i.e., la trasmisión de calor por convección es mucho más efectiva cerca del borde de entrada y justo tras la transición laminar-turbulento, luego en esas zonas la temperatura de la placa sería menor que en las demás zonas, para una distribución de fuentes más o menos uniforme..
Conviene recordar que este modelo matemático es una aproximación a la realidad, donde no habrá infinitos, ni discontinuidades, donde la transición puede tener lugar un poco antes o un poco después (y variar en la dirección transversal), dependiendo de detalles de la corriente de entrada, del borde, y del acabado superficial.
Podemos comprobar también los valores medios:
Si sopla de través.
| > | h2mean:=(1/L2)*Int(h[x],x=0..L2);h[x]=h2_;h[x=L]=subs(x=L2,dat,h2_);h2mean_:=subs(dat,int(h2_/L2,x=0..L2)); |
![`/`(`*`(Int(h[x], x = 0 .. L2)), `*`(L2))](images/p07_48.gif) |
![h[x] = `+`(`/`(`*`(6.199, `*`(`^`(`/`(`*`(x), `*`(m_)), `/`(1, 2)), `*`(kg_, `*`(m_)))), `*`(`^`(s_, 3), `*`(K_, `*`(x)))))](images/p07_49.gif) |
i.e., empieza en infinito, acaba en 11, y la media es 23, como ya se vio.
Si sopla a lo largo.
| > | h1mean:=(1/L1)*(Int(h[x,lam],x=0..xtr)+Int(h[x,turb],x=xtr..L1));h1mean_:=subs(dat,(1/L1)*(int(rhs(eqh1lam_),x=0..xt_)+int(rhs(eqh1turb_),x=xt_..L1))); |
![`/`(`*`(`+`(Int(h[x, lam], x = 0 .. xtr), Int(h[x, turb], x = xtr .. L1))), `*`(L1))](images/p07_52.gif) |
i.e., la media es 24,5, (antes dio 24,3; este 1% de incertidumbre es debido al redondeo en los coeficientes integrados).
| > |