>	restart:#"m12_p04"

Se desea estudiar el enfriamiento de una esfera maciza de hierro de 10 cm de diámetro, recién sacada de un horno a 150 °C, en una atmósfera a 20 °C. Se pide:

a) Flujo de calor por radiación, suponiendo e=0,2.

b) Flujo de calor por conducción suponiendo aire inmóvil, y cálculo del Nu equivalente.

c) Flujo de calor por convección natural, indicando los valores de Gr y Nu correspondientes.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Hierro_fundido":su2:="Aire":dat:=[D=0.1*m_,T1=(273+150)*K_,T0=(273+20)*K_,epsilon=0.2];

Esquema:

>

>

Eqs. const.:

>	s1dat:=get_sol_data(su1):Adat:=get_gas_data(su2):dat:=op(dat),Const,SI2,SI1:nu_:=subs(Adat,dat,mu*R*T0/p0);a_:=subs(Adat,dat,k*R*T0/(c[p]*p0));

a) Flujo de calor por radiación, suponiendo e=0,2.

Supondremos en todo momento que la esfera es isoterma, i.e. que la conducción interior es muy efectiva.

El flujo de calor irá variando con el tiempo, conforme se vaya enfriando la esfera.

El valor inicial será:

>	eq11_3;êqBE1:=subs(T[0]=T0,T=T1,%);eqBE1_:=subs(dat,evalf(subs(A=Pi*D^2,dat,%))):evalf(%,2);

i.e. inicialmente se pierden 8,8 W por intercambio radiativo con el entorno (supuesto cuerpo negro a T0).

b) Flujo de calor por conducción suponiendo aire inmóvil, y cálculo del Nu equivalent

>	eq11_7_3;eqBE2:=subs(R[1]=D/2,limit(%[1],R[2]=+infinity));eq12_2;eq11_2_0;eq3:=subs(A=4*Pi*R1^2,L=2*R1,solve({eqBE2,eq12_2,eq11_2_0},{Nus,Q,h}));eq3_:=evalf(subs(R1=D/2,DT=T1-T0,dat,Adat,eq3)):evalf(%,2);

i.e. el equivalente sería Nu=2, y se disiparían 2 W al aire.

c) Flujo de calor por convección natural, indicando los valores de Gr y Nu correspondientes.

>	eq12_1;eqNu:=subs(eq12_87);eqRa:=eq12_6;eqRa_:=subs(alpha=1/T0,L=D,DT=(T1-T0),nu=nu_,a=a_,Adat,dat,%);eqPr:=Pr=mu*c[p]/k;eqPr_:=subs(Adat,dat,%);eqNu_:=subs(eqRa_,eqPr_,eqNu);eqh:=h=k*Nus/D;eqh_:=subs(eqNu_,Adat,dat,%);eqBE_:=subs(dat,evalf(subs(eqh_,A=Pi*D^2,T[wall]=T1,T[fluid]=T0,dat,eq12_1)));

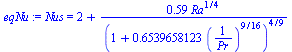i.e. al principio el flujo de calor es de unos 30 W

>