| > | restart:#"m12_p03" |
Se desea saber la pérdida de calor al ambiente de una tubería de 5 cm de diámetro y 1 cm de espesor de aislante de k=0,1 W/(m•K), por la que circula 0,01 kg/s de vapor que entra a 150 kPa y 150 °C. Se pide:
a) Números de Reynolds y Nusselt para el vapor.
b) Números de Grashof y Nusselt para el aire.
c) Flujo transversal de calor.
d) Variación axial de la temperatura del vapor.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su1:="H2O":su2:="Aire":dat:=[D=0.05*m_,DR=0.01*m_,k=0.1*W_/(m_*K_),mdot=0.01*kg_/s_,p1=150e3*Pa_,T1=(150+273)*K_]; |
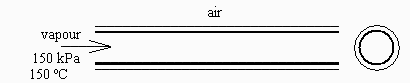
Esquema:
| > |
| > |
Eqs. const.:
| > | g1dat:=get_gas_data(su1);g2dat:=get_gas_data(su2);get_pv_data(su1):dat:=op(dat),Const,SI2,SI1: |
a) Números de Reynolds y Nusselt para el vapor.
| > | eqBM:=m=rho*v*A;eqBE:=Q=m*c[p]*DT;T1=subs(dat,T1);pvT1_:=subs(dat,evalf(subs(dat,pv(T1))));p1=subs(dat,p1);eq12_53;eqRe_:=evalf(subs(g1dat,dat,%));eqPr:=Pr=mu*c[p]/k;eqPr_:=subs(g1dat,dat,%);eq12_76;eqNu_:=subs(eqRe_,eqPr_,n=0.3,%);hv=k*Nus/D;eqhv_:=subs(eqNu_,g1dat,dat,%); |
i.e. Re=21000 (turbulento) y Nu=65.
b) Números de Grashof y Nusselt para el aire.
| > | eq12_5;eqMGI:=alpha=1/T;DTmax:=T1-T0;eqGr_:=subs(eqMGI,T=T0,DT=DTmax,L=D,nu=mu*(R*T0)/p0,g2dat,dat,eq12_5);eqNu:=eq12_86;eqPr_:=subs(g2dat,dat,eqPr);Ra:=Gr*Pr;eqNu_:=subs(eqGr_,eqPr_,eqNu);ha=k*Nus/D;eqha_:=subs(eqNu_,g2dat,dat,%);eqNu_simple:=Nus=0.53*'Ra'^(1/4);subs(eqGr_,eqPr_,eqNu_simple); |
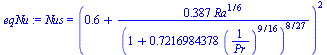 |
c) Flujo transversal de calor.
| > | eq12_1;eq5_43_1;eq11_7_2;eqBE1:=Q=hv*Pi*D*L*(T3-T1);eqBE2:=Q=k*2*Pi*L*(T4-T3)/ln((D+2*DR)/D);eqBE3:=Q=ha*Pi*(D+2*DR)*L*(T0-T4);sol_:=subs(dat,evalf(subs(eqhv_,eqha_,dat,solve({eqBE1,eqBE2,eqBE3},{T3,T4,Q})))); |
![Q = `+`(`/`(`*`(2, `*`(k, `*`(Pi, `*`(L, `*`(DT))))), `*`(ln(`/`(`*`(R[2]), `*`(R[1])))))), R = `+`(`/`(`*`(`/`(1, 2), `*`(ln(`/`(`*`(R[2]), `*`(R[1]))))), `*`(k, `*`(Pi, `*`(L)))))](images/p03_39.gif) |
i.e., el calor que sale, por unidad de longitud, es de unos 100 W/m, y las temperaturas son de 128 ºC en el interior del aislante, y de 71 ºC en su exterior (se ha despreciado la caída de temperatura en el espesor del tubo metálico).
Pero habíamos tomado un valor muy grande para el salto térmico en el aire; ahora vemos que como máximo será T0-T4.
Si repetimos todo el cálculo:
| > | DTmax:=T4-T0;eqGr_:=subs(eqMGI,T=T0,DT=DTmax,sol_,L=D,nu=mu*(R*T0)/p0,g2dat,dat,eq12_5);eqNu:=eq12_86;eqPr_:=subs(g2dat,dat,eqPr);Ra:=Gr*Pr;eqNu_:=subs(eqGr_,eqPr_,eqNu);ha=k*Nus/D;eqha_:=subs(eqNu_,g2dat,dat,%);eqNu_simple:=Nus=0.53*'Ra'^(1/4);subs(eqGr_,eqPr_,eqNu_simple);eq12_1;eq5_43_1;eq11_7_2;eqBE1:=Q=hv*Pi*D*L*(T3-T1);eqBE2:=Q=k*2*Pi*L*(T4-T3)/ln((D+2*DR)/D);eqBE3:=Q=ha*Pi*(D+2*DR)*L*(T0-T4);sol_:=subs(dat,evalf(subs(eqhv_,eqha_,dat,solve({eqBE1,eqBE2,eqBE3},{T3,T4,Q})))); |
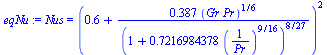 |
![Q = `+`(`/`(`*`(2, `*`(k, `*`(Pi, `*`(L, `*`(DT))))), `*`(ln(`/`(`*`(R[2]), `*`(R[1])))))), R = `+`(`/`(`*`(`/`(1, 2), `*`(ln(`/`(`*`(R[2]), `*`(R[1]))))), `*`(k, `*`(Pi, `*`(L)))))](images/p03_56.gif) |
i.e. las pérdidas no eran de 106 W/m sino de 95 W/m, y la temperatura exterior del aislante todavía era más baja de los 71 ºC; 353-288=66 ºC. Pero a la vista de las demás incertidumbres, ya no vale la pena seguir iterando.
d) Variación axial de la temperatura del vapor.
| > | Ts:=T1+Q/(mdot*c[p]);Ts_:=subs(sol_,g1dat,L=1*m_,dat,%);DT/L=subs(dat,Ts_-T1); |
i.e. la temperatura del vapor cae 5 ºC cada metro de tubería; como la variación es pequeña, la aproximación de la media por la de entrada sería buena si la longitud no es muy larga.
| > |