>	restart:#"m12_p01"

Se desea estimar el sobrecalentamiento, en régimen estacionario, de un gasto de 0,01 kg/s de R 12 que sale de un evaporador a 100 kPa y circula por un tubo de cobre de 0,5 mm de espesor, 10 mm de diámetro exterior y 50 cm de longitud, con una envoltura aislante de 5 mm de espesor de manta de fibra de vidrio, en presencia de una atmósfera a 30 °C. Datos: hR 12=250 W.m 2.K 1, kCu=390 W.m 1.K 1, kmanta=0,04 W.m 1.K 1, haire=10 W.m 2.K 1, cp,R 12= 580 J.kg 1.K 1. Se pide:

a) Temperatura, densidad y velocidad del R 12 a la entrada del conducto.

b) Balance energético y calor transmitido.

c) Temperatura de salida.

d) Comprobar, con las correlaciones empíricas generales, que las estimaciones dadas de hR 12 y haire son adecuadas.

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="CCl2F2":su2:="Cobre":su3:="Vidrio_(lana)":su4:="Aire":dat:=[mdot=0.01*kg_/s_,p1=100e3*Pa_,DR[1]=0.0005*m_,R=0.0045*m_,L=0.5*m_,DR[2]=0.005*m_,T0=(30+273)*K_,h[1]=250*W_/(m_^2*K_),h[2]=10*W_/(m_^2*K_)];

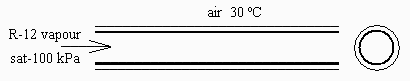
Esquema:

Eqs. const.

>	Gdat:=get_gas_data(su1):S1dat:=get_sol_data(su2):S2dat:=get_sol_data(su3):Adat:=get_gas_data(su4):get_pv_data(su1):dat:=op(dat),Const,SI2,SI1:kS1=subs(S1dat,k);kS2=subs(S2dat,k);

a) Temperatura, densidad y velocidad del R 12 a la entrada del conducto.

>	T1=Tv[p1];T1_:=subs(Gdat,T[b]);eqET:=eq1_12;eqET_:=subs(p=p1,T=T1_,Gdat,dat,%);eqm:=eq12_51;u_:=evalf(subs(eqET_,D=2*R,dat,solve(%,u)));

i.e. entra a -30 ºC, con 6 kg/m3, y a 26 m/s.

b) Balance energético y calor transmitido.

Se empieza suponiendo que las temperaturas no variarán mucho longitudinalmente (en realidad, no sñolo la temperatura del R12, sino la del cobre irá variando).

Se supone que los efectos de entrada son despreciables (para un tubo de D=9 mm, en los primeros 10 cm no se ha desarrollado el flujo):

Para hacerlo manualmente, convendría calcular cada una de las resistencias térmicas (aunque las que se ven despreciables se podrían obviar).

>

eqBE:=K*A*(T0-T1)=mdot*c[p]*(T2-T1);Q_1:=Qdot=(T0-Teais)/R1;Q_1:=Qdot=h[2]*2*Pi*(R+DR[1]+DR[2])*L*(T0-Teais);R1:=1/(h[2]*2*Pi*(R+DR[1]+DR[2])*L);R1_:=evalf(subs(dat,R1));eq11_7_2;Q_2:=Qdot=(Teais-Tiais)/R2;Q_2:=Qdot=(2*Pi*L*k[2]/ln((R+DR[1]+DR[2])/(R+DR[1])))*(Teais-Tiais);R2:=ln((R+DR[1]+DR[2])/(R+DR[1]))/(2*Pi*L*k[2]);R2_:=evalf(subs(dat,k[2]=k,S2dat,R2));Q_3:=Qdot=(Te-Ti)/R3;Q_3:=Qdot=(2*Pi*L*k[1]/ln((R+DR[1])/R))*(Te-Ti);R3:=ln((R+DR[1])/R)/(2*Pi*L*k[1]);R3_:=evalf(subs(dat,k[1]=k,S1dat,R3));Q_4:=Qdot=(Ti-T1)/R4;Q_4:=Qdot=h[1]*2*Pi*R*L*(Ta-Teais);R4:=1/(h[1]*2*Pi*R*L);R4_:=evalf(subs(dat,R4));Qdot:='(T0-T1)/(R1+R2+R3+R4)';Qdot_:=subs(dat,(T0-T1_)/(R1_+R2_+R3_+R4_));Teais_:=subs(dat,solve(subs(Qdot=Qdot_,dat,Q_1),Teais));Tiais_:=subs(dat,solve(subs(Qdot=Qdot_,Teais=Teais_,dat,k[2]=k,S2dat,Q_2),Tiais));Te=%;Ti_:=subs(dat,solve(subs(Qdot=Qdot_,Teais=Teais_,dat,k[1]=k,S1dat,Q_3),Ti));T1=T1_;Qdot:='Qdot':

i.e. tomando la temperatura del fluido igual a la de entrada, la de la pared de cobre sería casi 1 ºC mayor, y la del exterior del aislante unos 9 ºC sobre cero, siendo el flujo de calor total de casi 7 W.

Si se resuelve automáticamente es más sencillo:

>

eqBE1:=Qdot=h[1]*2*Pi*R*L*(Ti-T1);eqBE2:=Qdot=k1*2*Pi*L*(Te-Ti)/ln((R+DR[1])/R);eqBE3:=Qdot=k2*2*Pi*L*(Teais-Te)/ln((R+DR[1]+DR[2])/(R+DR[1]));eqBE4:=Qdot=h[2]*2*Pi*(R+DR[1]+DR[2])*L*(T0-Teais);sol_:=subs(dat,evalf(subs(T1=T1_,k1=k,S1dat,k2=k,S2dat,dat,solve({eqBE1,eqBE2,eqBE3,eqBE4},{Ti,Te,Teais,Qdot}))));

c) Temperatura de salida.

>	Ts:=T1+Qdot/(mdot*c[p]);c[p]=subs(Gdat,c[p]);Ts_:=subs(T1=T1_,sol_,Gdat,dat,Ts);DT=Ts_-T1_;

>

i.e. el vapor se calienta algo más de 1 ºC.

d) Comprobar, con las correlaciones empíricas generales, que las estimaciones dadas de hR 12 y haire son adecuadas.

Para el R12 usaremos la correlación de Dittus-Boelter de la convección forzada por el interior de tubos en régimen turbulento.

>	[mu,k]=subs(Gdat,[mu,k]);nu_:=subs(eqET_,Gdat,dat,mu/rho);a_:=subs(eqET_,Gdat,dat,k/(rho*c[p]));eqPr:=eq12_4;eqPr_:=subs(nu=nu_,a=a_,dat,%);eq12_50;eqRe_:=subs(u=u_,nu=nu_,D=2*R,dat,%);eq12_76;eqNu_:=subs(n=0.4,eqRe_,eqPr_,%);h1:=k*Nus/D;h1_:=subs(Gdat,eqNu_,D=2*R,dat,h1);

Efectivamente, Re>400 indica que el régimen es turbulento desarrollado, y vemos que, para el flujo de vapor de R12, sería más apropoado h=215 W/(m2·K) que los 250 W/(m2·K) asumidos.

Para el aire usaremos la correlación de Churchill-Chu de la convección natural alrededor de un cilindro horizontal (válida para cualquier régimen).

>

eqET_:=rho=subs(Adat,dat,p0/(R*T0));nu_:=subs(eqET_,Adat,dat,mu/rho);a_:=subs(eqET_,Adat,dat,k/(rho*c[p]));eqPr_:=subs(nu=nu_,a=a_,dat,eqPr);eq12_6;eqRa_:=subs(alpha=1/T0,L=2*(R+DR[1]+DR[2]),nu=nu_,a=a_,DT=T0-Teais_,sol_,dat,%);eq12_86;eqNu_:=subs(eqPr_,eqRa_,%);ha:=k*Nus/D;ha_:=subs(Adat,eqNu_,D=2*(R+DR[1]+DR[2]),dat,ha);

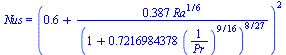i.e. sería mejor tomar h=6 W/(m2·K) que el valor asumido de h=10 W/(m2·K).

>