| > | restart:#"m11_p98" |
Considérese una tarjeta electrónica (PCB) de 1401001,5 mm3 de FR-4, con un recubrimiento de 50 m de cobre por cada lado, que en una de las caras es continuo, y en la otra sólo ocupa el 10% de la superficie, en la cual van montados tres circuitos integrados (IC), cada uno de 50203 mm3, disipando 5 W, con kIC=50 W/(m·K) de conductividad térmica, y CIC=20 J/K de capacidad térmica, y distribuidos uniformemente en la PCB (20 mm de separación entre ellos). Se supondrá que los lados cortos de la PCB tienen contacto térmico perfecto con paredes permanentemente a 25 ºC, y que los otros dos bordes están térmicamente aislados. Tómese para el FR-4 k=0,5 W/(m·K) en el plano y la mitad a su través. Se pide:
a) Considerando que la tarjeta sólo evacua calor por los bordes, determinar la temperatura máxima que se alcanzaría si toda la disipación estuviese uniformemente repartida en la PCB y los IC no influyeran.
b) Considerando que la tarjeta sólo evacua calor por los bordes, determinar la temperatura máxima que se alcanzaría con un modelo unidimensional en el que los IC llegaran hasta los bordes aislados, en el límite kIC, y con la kIC dada.
c) Considerando que se transmite calor por radiación, con una emisividad media de 0,7 por el lado de los componentes, y de 0,5 por la cara opuesta, con una caja electrónica que se puede suponer negra y a 45 ºC, determinar la temperatura máxima linealizando las pérdidas radiativas y con disipación uniforme.
d) Resolver el caso anterior pero sin linealizar y con la disipación no uniforme.
e) Resolver el problema térmico bidimensional estacionario y comparar el perfil central de temperaturas con el del caso anterior.
Data:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):interface(displayprecision=2):interface(rtablesize=infinity): |
| > | su1:="FR4":su2:="Cobre":dat:=[Lx=0.07*m_,Ly=0.1*m_,Lz=1.5e-3*m_,Lcu=50e-6*m_,f=0.1,Li1=0.02*m_,Li2=0.04*m_,Li3=0.06*m_,Lxic=0.02*m_,Lyic=0.04*m_,Lzic=3e-3*m_,Wic=5*W_,kic=50*W_/(m_*K_),Cic=20*J_/K_,Tb=(25+273.15)*K_,T0=(25+273.15)*K_,Tw=(45+273.15)*K_,epsilon1=0.7,epsilon2=0.5];To:=273.15: |
La simetría permite resolver solo la mitad (o la cuarta parte del área en 2D). No parece muy bueno el modelo 1D porque los IC no son muy largos.
F=FR-4, C=Cobre.
| > | datF:=rho=1850*kg_/m_^3,c=700*J_/(kg_*K_),k=0.5*W_/(m_*K_),kt=0.25*W_/(m_*K_);datC:=get_sol_data(su2);dat:=op(dat),Const,SI2,SI1: |
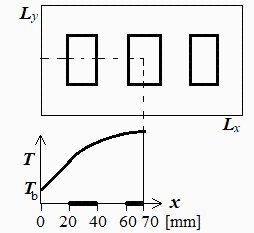
a) Considerando que la tarjeta sólo evacua calor por los bordes, determinar la temperatura máxima que se alcanzaría si toda la disipación estuviese uniformemente repartida en la PCB y los IC no influyeran.
Se trata de un problema 1D con phi=cte, cuya solución es parabólica con T(0)=Tb y Tp(L)=0:
| > | eqBE:=rho*c*Diff(T(x,t),t)=k*Diff(T(x,t),x,x)+phi;eqBEst:=0=k*Diff(T(x),x,x)+phi;eqT:=T=Tb+(phi*L/k)*x-(phi/(2*k))*x^2;phi=3*Wic/(2*Lx*Ly*Lz);eqphi:=subs(dat,%);eqkeff:=k=Sum(k[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqkeff:=k=(kC*f*Lcu+kF*(Lz-2*Lcu)+kC*Lcu)/(Lz);eqkeff_:=k=subs(kC=k,datC,kF=k,datF,dat,rhs(%));Tb_L_k_phi:=subs(dat,Tb),subs(dat,Lx),rhs(eqkeff_),subs(SI0,rhs(eqphi))*W_/m_^3;plot(subs(eqkeff_,eqphi,L=Lx,dat,SI0,rhs(eqT))-To,x=0..subs(dat,SI0,Lx),T_C=0..150);Tm:=subs(x=L,rhs(eqT));Tm_:=subs(eqkeff_,eqphi,L=Lx,dat,%);'Tm_'=TKC(%);eqCheck:=3*Wic=2*k*As*Tp0;As=Ly*Lz;As_:=subs(dat,Ly*Lz);Tp0=phi*L/k;Tp0_:=subs(eqkeff_,eqphi,dat,phi*Lx/k);eqCheck_:=subs(eqkeff_,Tp0=Tp0_,As=As_,dat,eqCheck); |
![k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delta[i], i)))](images/p98_11.gif) |
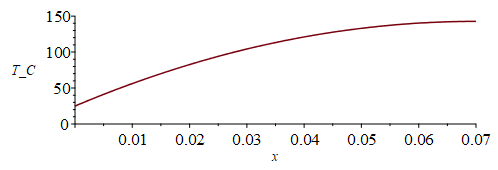 |
i.e. sería Tmax=143 ºC (demasiado alta para los IC y la PCB), si los 15 W estuviesen uniformemente repartidos. Y hemos verificado que toda la disipación sale por los extremos.
b) Considerando que la tarjeta sólo evacua calor por los bordes, determinar la temperatura máxima que se alcanzaría con un modelo unidimensional en el que los IC llegaran hasta los bordes aislados, en el límite kIC, y con la kIC dada.
Ahora T(x) será continua a trozos, con tramos rectos donde no hay IC, y tramos horizontales (si k=inf) o parabólicos sobre los IC.
Caso kic=inf.
| > | eqTs:=piecewise(x<Li1,Tb+(Ti1-Tb)*(x/Li1),x>Li1 and x<Li2,Ti1,x>Li2 and x<Li3,Ti2+(Ti3-Ti2)*(x-Li2)/(Li3-Li2),x>Li3 and x<Lx,Ti3);eqQi1:=k*As*(Ti1-Tb)/Li1=Wic+k*As*(Ti3-Ti2)/(Li3-Li2);Ti2=Ti1;eqQi2:=k*As*(Ti3-Ti2)/(Li3-Li2)=Wic/2;sol:=expand(solve(subs(Ti2=Ti1,{eqQi1,eqQi2}),{Ti1,Ti3}));sol_:=subs(eqkeff_,eqphi,As=As_,dat,sol);subs(Ti2=Ti1,sol_,eqkeff_,As=As_,dat,SI0,eqTs);plot(%-To,x=0..subs(dat,SI0,Lx),T_C=0..150);Tm_:=TKC(subs(sol_,Ti3)); |
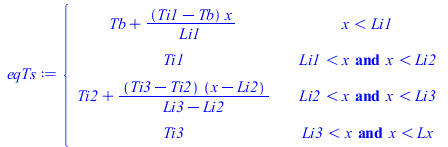 |
 |
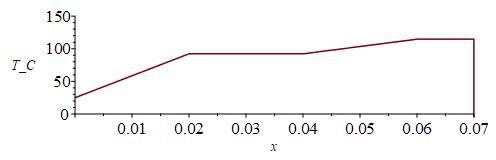 |
i.e. con kic=infinito solo se alcanzarían 115 ºC
Caso kic=50 W/(m·K). Pero hay que calcular la keff para Lz bajo los IC. Si mantenemos el área de paso, la keff será:
| > | eqkeffIC:=kIC=(kic*Lzic+kC*f*Lcu+kF*(Lz-2*Lcu)+kC*Lcu)/(Lz+2*Lcu);eqkeffIC_:=kIC=subs(kC=k,datC,kF=k,datF,dat,rhs(%));T12:=Ti1+a*(x-Li1)-(phiIC/(2*kIC))*(x-Li1)^2;eqTs:=piecewise(x<Li1,Tb+(Ti1-Tb)*(x/Li1),x>Li1 and x<Li2,T12,x>Li2 and x<Li3,Ti2+(Ti3-Ti2)*(x-Li2)/(Li3-Li2),x>Li3 and x<Lx,Ti3+phi*(Lx-Li3)*(x-Li3)/kIC-phi*(x-Li3)^2/(2*kIC)); |
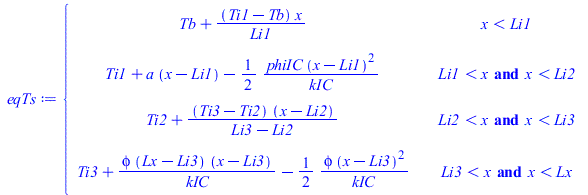 |
Tenemos 4 incógnitas: Ti1,Ti2,Ti3 y a. Las 4 condiciones son:
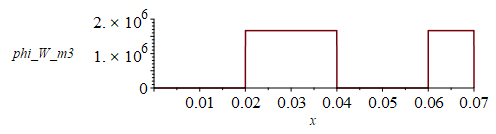
| > | eqQi1:=k*As*(Ti1-Tb)/Li1=Wic+k*As*(Ti3-Ti2)/(Li3-Li2);eqQi3:=k*As*(Ti3-Ti2)/(Li3-Li2)=Wic/2;eqTi2:=Ti2=subs(x=Li2,T12);eqQi2:=k*As*subs(x=Li1,diff(rhs(eqT),x))=subs(x=Li1,kIC*As*diff(T12,x));phiIC:=Wic/(Lxic*Ly*Lz);phiIC_:=subs(dat,%);eqphiss:=piecewise(x>Li1 and x<Li2,phiIC,x>Li3 and x<Lx,phiIC,0);plot(subs(dat,SI0,eqphiss),x=0..subs(dat,SI0,Lx),phi_W_m3=0..2e6); |
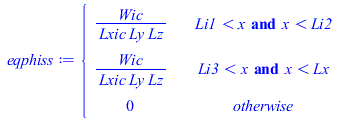 |
 |
y la solución es:
| > | sol_:=solve(subs(eqkeffIC_,eqkeff_,phi=phiIC_,As=As_,L=Lx,dat,SI0,{eqQi1,eqQi2,eqQi3,eqTi2}),{Ti1,Ti2,Ti3,a});eqTs_:=subs(sol_,eqkeffIC_,eqkeff_,phi=phiIC_,As=As_,L=Lx,dat,SI0,eqTs);plot(%-To,x=0..subs(dat,SI0,Lx),T_C=0..150);Tm_:=eval(subs(x=Lx-1e-6,dat,SI0,eqTs_))*K_;'Tm_'=TKC(%); |
 |
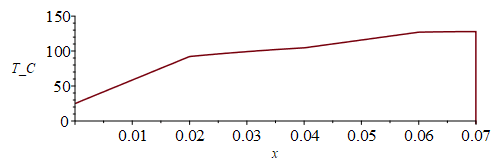 |
i.e. la Tmax es 128 ºC, que para kIC=infinito era 115 ºC. Todavía muy alta.
c) Considerando que se transmite calor por radiación, con una emisividad media de 0,7 por el lado de los componentes, y de 0,5 por la cara opuesta, con una caja electrónica que se puede suponer negra y a 45 ºC, determinar la temperatura máxima linealizando las pérdidas radiativas y con disipación uniforme.
En este caso existe solución analítica (ver Eq. 26 en Heat conduction).
| > | eqBE:=rho*c*As*Diff(T(x,t),t)=k*As*Diff(T(x,t),x,x)+phi*As-p*(epsilon1+epsilon2)*sigma*(T(x,t)^4-Tinf^4);eqBEst:=0=k*Diff(T(x),x,x)+phi-(p/As)*(epsilon1+epsilon2)*sigma*(T(x)^4-Tinf^4);eqBEstlin:=0=k*Diff(T(x),x,x)+phi-(p/As)*(epsilon1+epsilon2)*sigma*4*Tmean^3*(T(x)-Tinf);eqBEstlin:=0=Diff(T(x),x,x)+phi/k-(p*h/(k*As))*(T(x)-Tinf);eqh:=h=4*(epsilon1+epsilon2)*sigma*Tmean^3;eqm:=m=sqrt(p*h/(k*As));eqBEstlin:=0=diff(T(x),x,x)+phi/k-m^2*(T(x)-Tinf);eqTlin:=dsolve({%,T(0)=Tb,D(T)(L)=0},T(x)); |
Tomando una temperatura media para la PCB de 100 ºC (Tmean=373 K), y sustituyendo valores, las pérdidas radiativas en vacío (no dicen nada sobre si la caja va presurizada) serían:
| > | Tmean=373*K_;eqh_:=subs(%,dat,eqh);eqm_:=subs(%,p=Ly,eqkeff_,As=As_,dat,eqm);Tp0=3*Wic/(2*k*As);eqTlin_:=evalf(subs(%,eqkeff_,eqphi,eqm_,As=As_,Tinf=Tw,L=Lx,dat,SI0,eqTlin));plot([rhs(%)-To,subs(eqkeff_,eqphi,L=Lx,dat,SI0,rhs(eqT))-To],x=0..subs(dat,SI0,Lx),T_C=0..150);Tm_:=evalf(subs(x=Lx,dat,SI0,rhs(eqTlin_)))*K_;'Tm'=TKC(%);Q0:=k*As*Diff(T(x),x)[x=0];Q0_:=evalf(subs(x=0,eqkeff_,As=As_,SI0,k*As*diff(rhs(eqTlin_),x)))*W_; |
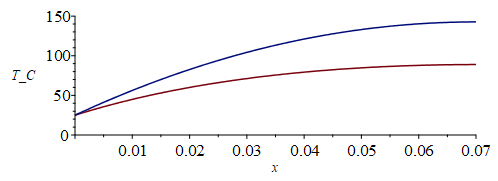 |
i.e. con radiación lineal la Tmax=89 ºC (en vez de 143 ºC del apartado a), cuya solución también se ha dibujado para comparar). Esto ya está en el límite de lo aceptable para IC normales. El calor que sale por conducción al encastre es 5,1 W (en vez de los 3Wic/2=7,5 W), luego han salido 2.4 W por radiación (ambas caras).
d) Resolver el caso anterior pero sin linealizar y con la disipación no uniforme.
Aquí solo vamos a hacer otra estimación, rebajando la Tmean de 100 ºC a 60 ºC que parece más apropiado, y luego lo resolveremos con Matlab.
| > | Tmean_approx:=333*K_;Qrad:=(epsilon1+epsilon2)*Lx*Ly*sigma*(Tmean^4-Tw^4);Qrad_:=subs(dat,(epsilon1+epsilon2)*Lx*Ly*sigma*(Tmean_approx^4-Tw^4));Tmax='Tb+(Tm-Tb)*(Wnet/Wtot)';Tmax_:=subs(dat,Tb+(Tm_-Tb)*((3*Wic-Qrad_)/(3*Wic)));'Tmax_'=TKC(%); |
i.e. ahora, de los 7,5 W disipados en media tarjeta, solo 1 W sale por radiación (ambas caras), y como la diferencia Tmax-Tb es proporcional a phi, resulta que la Tmax será de 85 ºC. Los resultados para la Tmax son parecidos, pero la discrepancia en Qrad es muy grande.
Las capacidades térmicas por unidad de volumen, rho·c, son:
| > | eqrceffIC:=rc=(rcic*Lzic+rcC*f*Lcu+rcF*(Lz-2*Lcu)+rcC*Lcu)/(Lz+2*Lcu);rcC_:=subs(datC,rho*c);rcF_:=subs(datF,rho*c);rcic_:=subs(dat,Cic/(Lxic*Lyic*Lzic));eqrceff_:=subs(rcC=rcC_,rcF=rcF_,rcic=0,dat,eqrceffIC);eqrceffIC_:=subs(rcC=rcC_,rcF=rcF_,rcic=rcic_,dat,eqrceffIC); |
i.e. 1,25e6 J/(m3·K) para la PCB y 16.9e6 J/(m3·K) donde están los IC, para los que se ha calculado rcIC=Cic/(Lxic*Lyic*Lzic).
Una estimación del tiempo de relajación de la PCB sola sería Dt=rho·c·(L/2)^2/k=1,25e6·0.07^2/15=410 s (con los IC será mayor).
La solución numérica en Matlab para este problema 1D discretizado en 80 tramos, con y sin pérdidas radiativas, es:

obteniendo en el estacionario (al cabo de 3000 s) un valor de Tmax=120 ºC sin radiación, y con pérdidas radiativas Tmax=90 ºC.
e) Resolver el problema térmico bidimensional estacionario y comparar el perfil central de temperaturas con el del caso anterior.
La solución numérica en Matlab para el problema 2D, da una Tmax=378 K=105 ºC, con los perfiles siguientes:

resultando ahora que se pierden 4,4 W por radiación y 10,6 W por conducción (para media tarjeta serían 2,2 W y 5,3 W. Nótese que la Tmax-2D=105 ºC es mayor que la Tmax-1D=90 ºC, como era de esperar por estar más concentrada la disipación.
| > |