Se desea enfriar un equipo de 90·45·40 mm3 que debe disipar 50 W y no debe sobrepasar Tmax=80 ºC en su superficie, estando alojado en un satélite geoestacionario. Se supondrá que la disipación es uniforme en todo el volumen del equipo, cuyas propiedades medias son =3000 kg/m3, c=1000 J/(kg·K), y k=100 W/(m·K). Se pide:
a) Pérdida de calor por radiación por las paredes del equipo en un recinto a Tr=25 ºC si su temperatura superficial es Tmax. Determinar el coeficiente convectivo equivalente.
b) Estimar el tiempo que se tardaría en alcanzar Tmax a partir de un estado inicial a Tr.
c) Mapa de temperaturas esperado en el equipo, en régimen estacionario, suponiendo despreciables las pérdidas por todas las paredes menos por una de las bases.
d) Se piensa montarlo centrado sobre un radiador que es una placa cuadrada de aluminio A6061 de 3 mm de espesor, aislada térmicamente del interior del satélite, y expuesta al vacío exterior por la otra cara, que está pintada de blanco. ¿Qué tamaño de placa haría falta si fuese isoterma?
e) ¿Y si le diese el sol de frente? ¿Qué tamaño de radiador haría falta, y qué pasaría cuando no le diese el sol?
f) Se va a tratar de usar como radiador una placa de 0,2 m de ancha (en vez de cuadrada), y se desea saber la longitud necesaria (sin sol). Establecer un modelo unidimensional de la trasmisión de calor a lo largo de la parte de placa que sobresale por cada lado, y resolver el problema analíticamente, linealizado las pérdidas radiativas.
g) Resolver numéricamente (sin linealizar) el problema 1D anterior. Resolver el problema no estacionario de la aleta partiendo de un estado inicial a Tr e imponiendo un incremento lineal de la temperatura en la raíz según el apartado b).
h) Resolver el problema 2D con una placa de 0,2·0,2 m2.
Datos:
| > |
read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):interface(displayprecision=2); |
| > |
su1:="H2O":dat:=[Wdis=50*W_,Tmax=(80+273.15)*K_,Tinf=2.7*K_,T0=(25+273.15)*K_,LzE=0.09*m_,LxE=0.045*m_,LyE=0.04*m_,LyAP=0.003*m_,LzAP=0.2*m_,E=1361*W_/m_^2,alpha=0.2,epsilon=0.85];dat:=op(dat),Const,SI2,SI1:Wdat:=get_liq_data(su1);Edat:=k=100*W_/(m_*K_),rho=3000*kg_/m_^3,c=1000*J_/(kg_*K_);A6dat:=k=180*W_/(m_*K_),rho=2710*kg_/m_^3,c=960*J_/(kg_*K_);A5dat:=k=140*W_/(m_*K_),rho=2680*kg_/m_^3,c=920*J_/(kg_*K_);Tf:=273.15: |
a) Pérdida de calor por radiación por las paredes del equipo en un recinto a Tr=25 ºC si su temperatura superficial es Tmax. Determinar el coeficiente convectivo equivalente.
El máximo será para superficies negras, incluyendo equipo y placa.
| > |
Qp:=Ap*sigma*(Tmax^4-T0^4);Ap:=2*(LxE*LzE+LzE*LyE+LxE*LyE);Ap_:=subs(dat,Ap);Qp_:=subs(dat,Qp);'Qp=Ap*he*(Tmax-Tinf)';he_:=subs(dat,Qp_/(Ap_*(Tmax-T0)));her:=4*epsilon*sigma*Tm^3;Tm_:=evalf(subs(dat,SI0,(he_/(4*epsilon*sigma))^(1/3)))*K_;'Tm_'=TKC(%); |
i.e. si todo el exterior del equipo estuviese a 80 ºC en un entorno a 25 ºC, se perderían 8,2 W por radiación, y el coeficiente convectivo equivalente al intercambio radiativo linealizado es he=7,9 W/(m2·K)., al que corresponde una Tmedia de 71 ºC, más próxima a Tmax=80 ºC que a Tr=25 ºC. A esto habría que añadir las pérdidas por conducción en los apoyos (y si no hubiera vacío las pérdidas por convección al fluido que lo rodeara).
b) Estimar el tiempo que se tardaría en alcanzar Tmax a partir de un estado inicial a Tr.
Una primera estimación sería suponer que el equipo se calienta uniformemente y todas sus paredes están aisladas, hasta alcanzar la Tmax.
| > |
eqBE0:=m*c*Diff(T,t)=Wdis;eqTB:=T(t)=T0+Wdis*t/(rho*V*c);tmin:=(Tmax-T0)*rho[E]*V[E]*c[E]/Wdis;V[E]:=LxE*LyE*LzE;mE_:=subs(Edat,dat,rho*%);tmin_:=subs(rho[E]=rho,c[E]=c,Edat,dat,tmin); |
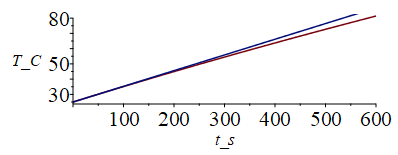
i.e. si estubiera aislado por fuera, pasaría de 25 ºC a 80 ºC en 530 s (9 min). Si se contabilizan las pérdidas radiativas, pero linealizadas, el resultado sería algo mayor. La evolución de la T_Equipo sería prácticamente lineal en ambos casos:
| > |
eqT:=dsolve([mc*diff(T(t),t)=Wdis-hA*(T(t)-T0),T(0)=T0],T(t));plot(subs(t=t_s,mc=mE_*c,hA=he_*Ap_,Edat,dat,SI0,[rhs(%)-Tf,T0+Wdis*t/mc-Tf]),t_s=0..600,T_C=25..80);tmin__:=evalf(subs(mc=mE_*c,hA=he_*Ap_,Edat,dat,SI0,solve(Tmax=rhs(eqT),t)))*s_; |
i.e. si estubiera aislado por fuera, pasaría de 25 ºC a 80 ºC en 530 s (xasi 9 min), y con las pérdidas radiativas 580 s (casi 10 min).
c) Mapa de temperaturas esperado en el equipo, en régimen estacionario, suponiendo despreciables las pérdidas por todas las paredes menos por una de las bases.
Se trata de un problema 1D que admite solución analítica. El problema es similar al de una varilla de longitud L=LyE=0,04 m con una disipación de energía uniforme de valor total 100 W, con un extremo a 70 ºC térmicamente aislado (hemos despreciado las pérdidas radiativas) y el otro extremo a una temperatura T tal que fluya por ahí todo el calor. Sea Ac el área de la cara por donde sale el calor. Tomando el origen en el extremo aislado:
| > |
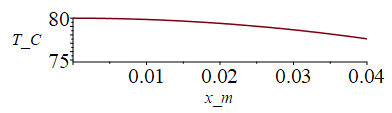
eqHeat:=0=k*Diff(T,x,x)+phi;eq0:=T(x=0)=T0;eq0p:=k*As*Diff(T,x)[x=0]=0;eqL:=T(x=L)=TL;eqLp:=k*As*Diff(T,x)[x=L]=-Wdis;eqT:=T(x)=T0-Q*x^2/(2*k*L*A);L=LyE;L_:=subs(dat,LyE);k=kE;k=subs(Edat,k);Ac:=LxE*LzE;Ac_:=subs(dat,Ac);'Ac_'=%*1e4*cm_^2/m_^2;Q=Wdis;eqT_:=T(x)=subs(Edat,dat,Tmax-Wdis*x^2/(2*k*L_*Ac_));eqTL:=T[x=L]=subs(x=L_,rhs(%));Tc_:=rhs(%);'Tc_'=TKC(%);plot(subs(x=x_m,SI0,rhs(eqT_)-Tf),x_m=0..L_/m_,T_C=75..80); |
i.e. la grans conductividad interior hace que el equipo sea casi isotermo. Para que la temperatura en la cara más caliente no supere los 80 ºC, la cara fría ha de estar como máximo a Tc=77,5 ºC. El estado transitorio T(x,t) se resolvería numéricamente
d) Se piensa montarlo centrado sobre una placa cuadrada de aluminio A6061 de 3 mm de espesor, aislada térmicamente del interior del satélite, y expuesta al vacío por la otra cara, que está pintada de blanco. ¿Qué tamaño de placa haría falta si fuese isoterma?
Si toda la placa estuviese a la temperatura anterior:
| > |
eqBE:=Qin=Qout;eqBE:=Wdis=epsilon*A*sigma*(Tc^4-Tinf^4);Tc=Tc_;A_:=subs(Tc=Tc_,dat,solve(eqBE,A));Lsquare_:=subs(SI0,sqrt(%))*m_;mAP:=subs(A6dat,dat,rho*LyAP*Lsquare_^2); |
i.e. se necesitaría una placa de 0,26 m de lado estando a 77,5 ºC para evacuar los 50 W. La masa de la placa sería de 0,56 kg. El espesor no ha intervenido en el cálculo, así que podría hacerse más delgada.
e) ¿Y si le diese el sol de frente? ¿Qué tamaño de radiador haría falta, y qué pasaría cuando no le diese el sol?
Tomando valores típicos para la irradiancia solar y para la absortancia solar, el balance energético da:
| > |
eqBE:=Qin=Qout;eqBE:=Wdis+alpha*E*A=epsilon*A*sigma*(Tc^4-Tinf^4);Tc=Tc_;A__:=subs(Tc=Tc_,dat,solve(eqBE,A));Lsquare__:=subs(SI0,sqrt(%))*m_;mAP:=subs(A6dat,dat,rho*LyAP*Lsquare__^2);eqBE_:=subs(E=0,eqBE);Tc__:=(subs(A=A__,dat,SI0,solve(%,Tc^4)))^(1/4)*K_;'Tc__'=TKC(%); |
![Typesetting:-mprintslash([eqBE := Qin = Qout], [Qin = Qout])](images/p96_51.gif) |
![Typesetting:-mprintslash([eqBE := `+`(`*`(A, `*`(E, `*`(alpha))), Wdis) = `*`(epsilon, `*`(A, `*`(sigma, `*`(`+`(`*`(`^`(Tc, 4)), `-`(`*`(`^`(Tinf, 4))))))))], [`+`(`*`(A, `*`(E, `*`(alpha))), Wdis) =...](images/p96_52.gif) |
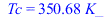 |
![Typesetting:-mprintslash([A__ := `+`(`*`(.1094881793, `*`(`^`(m_, 2))))], [`+`(`*`(.1094881793, `*`(`^`(m_, 2))))])](images/p96_54.gif) |
![Typesetting:-mprintslash([Lsquare__ := `+`(`*`(.3308899807, `*`(m_)))], [`+`(`*`(.3308899807, `*`(m_)))])](images/p96_55.gif) |
![Typesetting:-mprintslash([mAP := `+`(`*`(.8901388977, `*`(kg_)))], [`+`(`*`(.8901388977, `*`(kg_)))])](images/p96_56.gif) |
![Typesetting:-mprintslash([eqBE_ := Wdis = `*`(epsilon, `*`(A, `*`(sigma, `*`(`+`(`*`(`^`(Tc, 4)), `-`(`*`(`^`(Tinf, 4))))))))], [Wdis = `*`(epsilon, `*`(A, `*`(sigma, `*`(`+`(`*`(`^`(Tc, 4)), `-`(`*`(...](images/p96_57.gif) |
| Warning, solving for expressions other than names or functions is not recommended. |
![Typesetting:-mprintslash([Tc__ := `+`(`*`(311.9968412, `*`(K_)))], [`+`(`*`(311.9968412, `*`(K_)))])](images/p96_58.gif) |
 |
(5) |
i.e. con el sol de frente hace falta un radiador mayor, de 0,11 m2 en vez de 0,07 m2, para mantener Tmax=80 ºC (Tc=77,5 ºC). Pero entonces cuando no le diera el sol el equipo se enfriaría hasta Tc=39 ºC. La masa del radiador sería ahora de 0,9 kg. También habría que tener en cuenta que la irradiancia solar es mayor a principios de año, y que la absortancia aumenta con los años de servicio, lo cual podría incluso hacer inviable el radiador (i.e. que en lugar de enfriar calentara el equipo).
f) Se va a tratar de usar como radiador una placa de 0,20 m de ancha (en vez de cuadrada), y se desea saber la longitud necesaria (sin sol). Establecer un modelo unidimensional de la trasmisión de calor a lo largo de la parte de placa que sobresale por cada lado, y resolver el problema analíticamente, linealizado las pérdidas radiativas.
Con el modelo de radiador isotermo, la placa de 0,2 m de ancho habría de tener A/L=0,07/0,20=0,34 m de longitud total, que descontando los 45 mm del equipo sobresaldría (0.34-0.045)/2=0,15 m por cada lado. Pero estas 'aletas' no serán isotermas. Para empezar, supondremos que el tramo en contacto con el equipo es isotermo, con los Tc=77,5 ºC antes calculados, porque en él es muy grande la conductividad equivalente a causa del equipo. El calor que ha de evacuar cada aleta será la mitad de los 50 W, una vez descontados los que se evacúan bajo el equipo (en realidad se debería extender a las zonas adyacentes que se consideran isotermas en este modelo 1D). Para los tramos que sobresalen, si las pérdidas son lineales, la solución analítica viene en HT-Rods and fins.
| > |
eqBE:=0=k*A*diff(T(x),x,x)-h*p*(T(x)-Tinf);eqT:=T(x)=Tinf+(Troot-Tinf)*cosh(m*(L-x))/cosh(m*L);eqm:=m=sqrt(h*p/(k*A));Qroot:=(Troot-Tinf)*sqrt(p*h*k*A)*tanh(m*L);eqeta:=eta=tanh(m*L)/(m*L); |
con los valores siguientes:
| > |
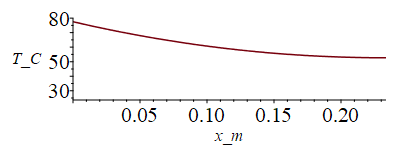
eqQroot:='Qroot=(Wdis-QoutAc)/2';QoutAc:='Ac'*sigma*(Tc^4-Tinf^4);QoutAc_:=subs(Tc=Tc_,dat,%);Qroot_:=subs(Tc=Tc_,dat,rhs(eqQroot));'Tinf'=subs(dat,Tinf);Troot=Tc_;eqh:=h=4*sigma*Tm^3;Tm='(Tc-Tinf)/2';Tm_:=subs(dat,(Tc_-Tinf)/2);Tm_:=subs(dat,SI0,T0^3/4)^(1/3)*K_;eqh_:=subs(Tm=Tm_,dat,eqh);eqp:=p=LzAP;eqp_:=p=subs(dat,LzAP);k=subs(A6dat,k);eqA:=A=LzAP*LyAP;eqA_:=subs(dat,%);'A'=rhs(%)*1e4*cm_^2/m_^2;eqm_:=m=evalf(subs(eqA_,eqh_,eqp_,A6dat,SI0,rhs(eqm)))/m_;eqQroot_:=evalf(subs(Troot=Tc_,eqp_,eqh_,eqA_,eqm_,A6dat,dat,SI0,lhs(eqQroot)=Qroot_));Lfin_:=solve(%,L)*m_;At:=LzAP*(LxE+2*Lfin);At_:=subs(Lfin=Lfin_,dat,%);mAP:=subs(A6dat,dat,rho*LzAP*LyAP*(LxE+2*Lfin_));eqT_:=evalf(subs(Troot=Tc_,eqm_,L=Lfin_,dat,SI0,eqT));plot(subs(x=x_m,rhs(%))-Tf,x_m=0..Lfin_/m_,T_C=25..80);Tmin_:=evalf(subs(x=Lfin_,SI0,rhs(eqT_)))*K_;'Tmin_'=TKC(%);eqQ0check:='Q0'=k*LzAP*LyAP*Diff(rhs(eqT_),x)[x=0];'Q0'=evalf(subs(x=0,A6dat,dat,SI0,k*LzAP*LyAP*diff(rhs(eqT_),x)))*W_;eqRadCheck:=Tmean^4='Q0'/(epsilon*LzAP*Lfin*sigma);Tmean_:=subs(Lfin=Lfin_,dat,SI0,(Qroot_/((epsilon*LzAP*Lfin*sigma))))^(1/4)*K_;'Tmean_'=TKC(%); |
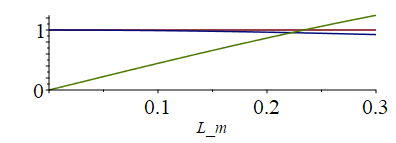
i.e. la placa de aluminio de 3 mm de espesor y 0,2 m de ancho, debería sobresalir Lfin=0,23 m por cada lado (en total mediría 0,23+0,045+0,23=0,5 m de largo. Esa es una pobre solución al problema térmico de enfriar un equipo de 9·4,5·4 cm3; comvendría hacer más isotermo el radiador usando conductos de calor (heat pipes) internos o externos. El área total es ahora bastante mayor que en el caso isotermo (0,10 frente a 0,07) porque la eficiencia de las aletas es menor que la unidad, al ir decreciendo la T(x). Si representamos la eficiencia y el calor evacuado (dividido por el valor deseado, 48,3 W), en función de la longitud de aleta, L, tenemos:
| > |
plot(subs(L=L_m,eqm_,SI0,[1,rhs(eqeta),lhs(eqQroot_)/Qroot_]),L_m=0..0.3); |
que muestra cómo crece el calor evacuado con el tamaño (se podría comprobar que aparece una asíntota para L muy grandes (y la eficiencia tiende a 0).
g) Resolver numéricamente (sin linealizar) el problema 1D anterior. Resolver el problema no estacionario de la aleta partiendo de un estado inicial a Tr e imponiendo un incremento lineal de la temperatura en la raíz según el apartado b).
El problema radiativo no linealizado se ha programado en Matlab. Manteniendo el tamaño de aleta calculado con el modelo lineal, Lfin=0,23 m, la simulación da:

donde en T(t) se ve cómo evolucionan con el tiemp la T en 20 puntos equiespaciados, y en T(x) cómo evoluciona con el perfil de T con el tiempo, habiemdo superpuesto con '+' la solución analítica antes calculada. Aunque parece que el resultado numérico coincide perfectamente con el modelo linealizado, resulta que se evacúa algo más de calor en el caso no linealizado (27,1 W en vez de los 23,3 W de diseño), lo cual permitiría reducir la longitud de la aleta hasta Lfin=0,19 m, que no es desdeñable.
h) Resolver el problema 2D con una placa de 0,2·0,2 m2.
La solución con Matlab para un radiador de 0,2·0,2 m2 con la zona central (de 9·4,5 cm2) a 77,5 ºC, cuando se alcanza el régimen estacionario, es:
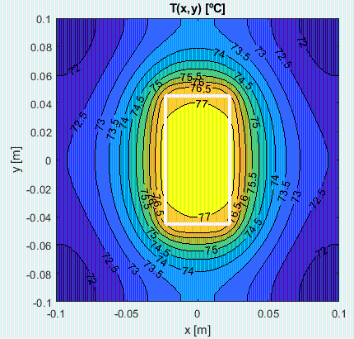
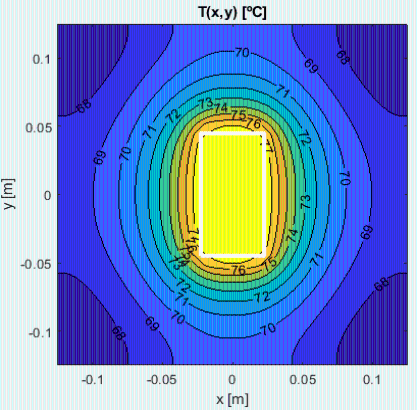
con una Tmin=72 ºC (en las puntas). Pero resulta que esa placa de 0,2·0,2 m2 no es capaz de evacuar mas que 30 W, lo cual era de esperar porque ya en el apartado d) vimos que como mínimo se necesitaría una placa de 0,26·0,26 m2. La simulación 2D demanda una placa de 0,27·0,27 m2 para evacuar los 50 W, quedando las esquinas a 66 ºC.
La simulación con elementos finitos no requiere malla estructurada. La solución imponiendo T=77,5 ºC en el contorno interior es:
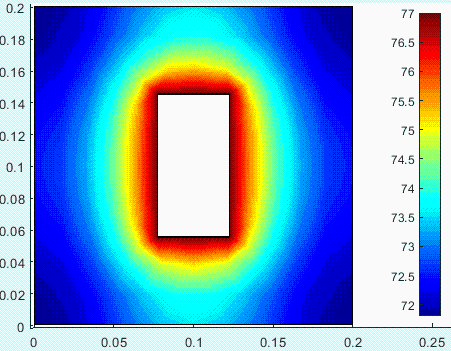
![Typesetting:-mprintslash([eqT := T(t) = `+`(T0, `/`(`*`(Wdis), `*`(hA)), `-`(`/`(`*`(exp(`+`(`-`(`/`(`*`(hA, `*`(t)), `*`(mc))))), `*`(Wdis)), `*`(hA))))], [T(t) = `+`(T0, `/`(`*`(Wdis), `*`(hA)), `-`...](images/p96_23.gif)