| > | restart:#"m11_p94.mw" |
ConsidÃĐrese una tarjeta electrÃģnica (PCB) de 100ïī100 mm2, compuesta por un laminado de FR-4 de 0,5 mm de espesor, recubierta por ambas caras con 70 ïm de espesor de cobre. En la cara superior, donde van montados los componentes electrÃģnicos, el cobre solo ocupa un 50 % de la superficie (las pistas de conexiones). La PCB lleva montado un gran circuito integrado programable (una FPGA) de 50ïī50 mm2, centrado en la tarjeta y con buen contacto tÃĐrmico con ella, que disipa 10 W, empaquetado en nitruro de aluminio (AlN) y con 1 mm de espesor total. Suponiendo que solo un borde de la PCB estÃĄ conectado a la placa base, el cual va a estar permanentemente a 30 šC, que los otros bordes apenas transmiten calor, y con la tabla adjunta de propiedades de los materiales, se pide:
a) Determinar la conductividad tÃĐrmica efectiva perpendicular a la PCB y el salto de temperaturas si todo el calor disipado fluyera perpendicularmente.
b) Determinar la conductividad tÃĐrmica efectiva paralela a la placa, y la distribuciÃģn de temperatura en la placa, suponiendo la disipaciÃģn total uniformemente distribuida en toda el ÃĄrea de la PCB, y que solo cuenta la conducciÃģn tÃĐrmica de la PCB.
c) Resolver analÃticamente el problema de conducciÃģn unidimensional en la direcciÃģn longitudinal (x) con una distribuciÃģn de fuentes correspondiente a la integral en la direcciÃģn transversal (y), suponiendo que solo hay conducciÃģn a travÃĐs de la PCB.
d) Volver a resolver el apartado anterior aÃąadiendo el efecto de la conductividad a travÃĐs de la FPGA.
e) Volver a resolver el apartado anterior aÃąadiendo el efecto de la radiaciÃģn tÃĐrmica por ambas caras con una carcasa que estÃĄ a 40 šC, con el modelo de cuerpos negro linealizado.
f) Resolver numÃĐricamente el apartado anterior en el caso no estacionario de encendido desde el reposo, considerando que la temperatura inicial es de 30 šC.
g) Resolver el caso bidimensional estacionario.

| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su1:="FR4":su2:="Cobre":su3:="AlN":dat:=[L=0.1*m_,LzF=0.5e-3*m_,LzC=70e-6*m_,f=0.5,LN=0.05*m_,LzN=1e-3*m_,QN=10*W_,Tb=(30+273.15)*K_,Tinf=(40+273.15)*K_,epsilon=1];Lz_:=subs(dat,LzF+2*LzC); |
Eqs. const. (F=FR-4, C=Cobre, N=AlN):
| > | datF:=rho=1850*kg_/m_^3,c=700*J_/(kg_*K_),k=0.5*W_/(m_*K_),kt=0.25*W_/(m_*K_);datC:=get_sol_data(su2);datN:=rho=3200*kg_/m_^3,c=735*J_/(kg_*K_),k=150*W_/(m_*K_);dat:=Lz=Lz_,op(dat),Const,SI2,SI1: |
a) Determinar la conductividad tÃĐrmica efectiva perpendicular a la PCB y el salto de temperaturas si todo el calor disipado fluyera perpendicularmente.
Basta considerar la FR-4 puesto que las otras capas son mucho mÃĄs conductoras del calor.
| > | eqQ:=Q=k*A*DT/delta;DT:=QN*LzF/(k*AN);k=subs(datF,kt);eqAN:=AN=LN^2;eqAN_:=subs(dat,%);DT_:=subs(eqAN_,k=kt,datF,dat,DT); |
i.e. el salto de temperatura de un lado a otro en el centro de la PCB eserÃĄ de 8 šC. Si consideramos todo el camino del calor desde las uniones del circuito integrado (incluso suponiÃĐndolas lo mÃĄs alejadas, aunque estarÃĄn por un nivel intermedio), la conductividad tÃĐrmica efectiva para el camino total, y el salto DT, suponiendo que todo el calor fluye en esa Única direcciÃģn, serÃa:
| > | eqkeff_acrossPCB:=k=Sum(delta[i],i)/Sum(delta[i]/k[i]*f[i],i);eqkeff_acrossPCB:=k=(Lz+LzN)/(LzC/kC+LzF/ktF+LzC/(kC*f)+LzN/kN);eqkeff_acrossPCB_:=k=subs(kC=k,datC,ktF=kt,datF,kN=k,datN,dat,rhs(%));DT:=QN*(Lz+LzN)/(k*AN);DT_:=subs(eqAN_,eqkeff_acrossPCB_,datF,dat,DT); |
![Typesetting:-mprintslash([eqkeff_acrossPCB := k = `/`(`*`(Sum(delta[i], i)), `*`(Sum(`/`(`*`(delta[i], `*`(f[i])), `*`(k[i])), i)))], [k = `/`(`*`(Sum(delta[i], i)), `*`(Sum(`/`(`*`(delta[i], `*`(f[i]...](images/p94_13.gif) |
![Typesetting:-mprintslash([eqkeff_acrossPCB := k = `/`(`*`(`+`(Lz, LzN)), `*`(`+`(`/`(`*`(LzC), `*`(kC)), `/`(`*`(LzF), `*`(ktF)), `/`(`*`(LzC), `*`(kC, `*`(f))), `/`(`*`(LzN), `*`(kN)))))], [k = `/`(`...](images/p94_14.gif) |
i.e. apenas hay diferencia.
b) Determinar la conductividad tÃĐrmica efectiva paralela a la placa, y la distribuciÃģn de temperatura en la placa, suponiendo la disipaciÃģn total uniformemente distribuida en toda el ÃĄrea de la PCB, y que solo cuenta la conducciÃģn tÃĐrmica de la PCB.
Sin tener en cuenta la conductividad en la FPGA:
| > | eqkeff_alongPCB:=k=Sum(k[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqkeff_alongPCB:=k=(kC*(1+f)*LzC+kF*LzF)/Lz;eqkeff_alongPCB_:=k=subs(kC=k,datC,kF=k,datF,dat,rhs(%)); |
![Typesetting:-mprintslash([eqkeff_alongPCB := k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delta[i], i)))], [k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delta...](images/p94_18.gif) |
i.e. la conductividad tÃĐrmica efectiva paralela a la placa es k=65 W/(m·K). PodrÃa comprobarse que la FR-4 apenas influye. Para el perfil de temperatura correspondiente a una distribuciÃģn uniforme de fuentes y con esa conductividad:
| > | To:=273.15:eqT:=T=Tb+(QN/k)*(x/(Ly*Lz)-x^2/(2*Lx*Ly*Lz));eqT_:=subs(eqkeff_alongPCB_,Lx=L,Ly=L,dat,SI0,eqT);plot(rhs(eqT_)-To,x=0..subs(dat,SI0,L),T_C=30..150);Tm:=Tb+QN/(k*Lz)-QN/(2*k*Lz);Tm_:=subs(eqkeff_alongPCB_,dat,%);'Tm_'=TKC(%);Tp0:=Diff(T,x)[x=0];Tp0:=subs(x=0,diff(rhs(eqT),x));Tp0_:=subs(eqkeff_alongPCB_,Ly=L,dat,%);Tp0__:=subs(x=0,diff(rhs(eqT_),x))*K_/m_; |
![Typesetting:-mprintslash([eqT := T = `+`(Tb, `/`(`*`(QN, `*`(`+`(`/`(`*`(x), `*`(Ly, `*`(Lz))), `-`(`/`(`*`(`/`(1, 2), `*`(`^`(x, 2))), `*`(Lx, `*`(Ly, `*`(Lz)))))))), `*`(k)))], [T = `+`(Tb, `/`(`*`(...](images/p94_21.gif) |
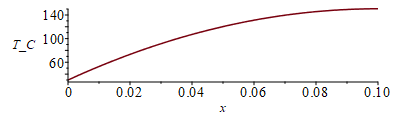 |
i.e. un perfil parabÃģlico con una Tmax=150 šC, que es muy alta para una PCB normal (no suelen superar los 100 šC). Hemos calculado la pendiente de T(x) en el encastre para comprobaciÃģn.
c) Resolver analÃticamente el problema de conducciÃģn unidimensional en la direcciÃģn longitudinal (x) con una distribuciÃģn de fuentes correspondiente a la integral en la direcciÃģn transversal (y), suponiendo que solo hay conducciÃģn a travÃĐs de la PCB.
La distribuciÃģn de los Q=10 W a lo largo del eje x serÃa nula donde no proyecta segÚn el eje 'y' la FPGA, y de valor QN/LN=10/0,05)=200 W/m en la parte central. El perfil de temperaturas lo obtenemos empalmando las soluciones a trozos, i.e. obligando a que en x=xi=(L-LN)/2=25 mm, haya la misma T y la misma Q.
Si tomamos el origen de x en donde empieza la FPGA para usar la expresiÃģn anterior para el tramo parabÃģlico, y sabiendo que el tramo final serÃĄ isotermo por no haber flujo de calor, y de valor Tm=T2x[LI]:
| > | QNx_:=piecewise(x<0,0,x>0.05,0,subs(dat,SI0,QN/LN));plot(%,x=-0.025..0.075,QNx_W_m=0..200);T1x:=Ti+(Ti-Tb)*2*x/(L-LN);T2x:=subs(Tb=Ti,Lx=LN,rhs(eqT));eqQi:=k1*A1*Diff(Tx1,x)[x=0]=k2*A2*Diff(Tx2,x)[x=0];eqQi:=subs(x=0,Ly=L,k*L*Lz*diff(T1x,x)=k*L*Lz*diff(T2x,x));Ti_:=subs(eqkeff_alongPCB_,dat,solve(%,Ti));'Ti_'=TKC(%);Tm:='T2x'[x=LN];Tm:=subs(x=LN,Ti=Ti_,Ly=L,eqkeff_alongPCB_,dat,T2x);'Tm'=TKC(%);T123_:=subs(Ti=Ti_,Lx=L,Ly=L,eqkeff_alongPCB_,dat,SI0,piecewise(x<0,T1x,x>0.05,Tm,T2x)):plot(T123_-To,x=-0.025..0.075,T_C=30..150); |
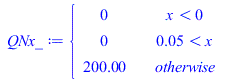 |
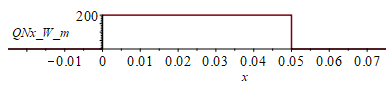 |
![Typesetting:-mprintslash([T2x := `+`(Ti, `/`(`*`(QN, `*`(`+`(`/`(`*`(x), `*`(Ly, `*`(Lz))), `-`(`/`(`*`(`/`(1, 2), `*`(`^`(x, 2))), `*`(LN, `*`(Ly, `*`(Lz)))))))), `*`(k)))], [`+`(Ti, `/`(`*`(QN, `*`(...](images/p94_34.gif) |
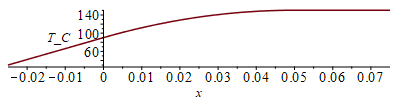 |
i.e. la Tmax no cambia (la concentraciÃģn de la disipaciÃģn en una zona zentral mÃĄs pequeÃąa no modifica la Tmax, incluso si toda la disipaciÃģn estuviera concentrada en la lÃnea media, i.e. en x=Lx/2).
d) Volver a resolver el apartado anterior aÃąadiendo el efecto de la conductividad a travÃĐs de la FPGA.
El modelo anterior de conductividad tÃĐrmica efectiva uniforme no es bueno porque en el contacto con la FPGA el camino tÃĐrmico se ensancha, lo que puede contabilizarse tambiÃĐn manteniendo el espesor del camino fijo, Lz=LzPCB, y aumentando la k efectiva. El contacto tÃĐrmico de la FPGA con la PCB es muy bueno porque suele ser con una matriz de bolitas de soldadura (BGA) de un milÃmetro de separaciÃģn, i.e. de unos 50·50=2500 contactos para un chip de 50·50 mm2.
Si la FPGA cubriese toda la placa, la conductividad efectiva serÃa:
| > | eqkeff_underFPGA:=k=Sum(k[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqkeff_underFPGA:=k=(kC*(1+f)*LzC+kF*LzF+kN*LzN)/Lz;eqkeff_underFPGA_:=k=subs(kC=k,datC,kF=k,datF,kN=k,datN,dat,rhs(%)); |
![Typesetting:-mprintslash([eqkeff_underFPGA := k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delta[i], i)))], [k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delt...](images/p94_43.gif) |
pero como la FPGA sÃģlo cubre la mitad de la profundidad en 'y', habrÃĄ que tomar la semisuma, y el perfil de conductividades k(x) serÃa:
| > | eqkeff_underFPGA_:=k=(rhs(eqkeff_alongPCB_)+rhs(eqkeff_underFPGA_))/2;k_:=subs(SI0,piecewise(x<0,rhs(eqkeff_alongPCB_),x>0.05,rhs(eqkeff_alongPCB_),rhs(eqkeff_underFPGA_)));plot(k_,x=-0.025..0.075,k=30..200); |
![Typesetting:-mprintslash([k_ := PIECEWISE([64.86718750, `<`(x, 0)], [64.86718750, `<`(0.5e-1, x)], [182.0546876, otherwise])], [piecewise(`<`(x, 0), 64.86718750, `<`(0.5e-1, x), 64.86718750, 182.05468...](images/p94_47.gif) |
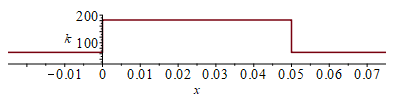 |
por lo que el nuevo perfil de T(x) serÃa ahora:
| > | eqQi:=k1*A1*Diff(Tx1,x)[x=0]=k2*A2*Diff(Tx2,x)[x=0];eqQi:=subs(x=0,Ly=L,k1*L*Lz*diff(T1x,x)=k*L*Lz*diff(T2x,x));Ti_:=subs(k1=k,eqkeff_alongPCB_,k2=k,eqkeff_underFPGA_,dat,solve(%,Ti));'Ti_'=TKC(%);Tm_:=subs(x=LN,Ti=Ti_,Lx=L,Ly=L,eqkeff_underFPGA_,dat,SI0,T2x)*K_;'Tm_'=TKC(%);T123__:=subs(Ti=Ti_,Lx=L,Ly=L,eqkeff_underFPGA_,dat,SI0,piecewise(x<0,T1x,x>0.05,Tm_,T2x)):plot(T123__-To,x=-0.025..0.075,T_C=30..150); |
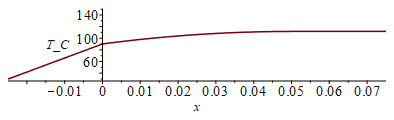 |
que como se ve es mÃĄs plano; la Tmax ha bajado de los 150 šC anteriores a 112 šC por la mayor conductividad de la FPGA. Como era de esperar, la Ti (comienzo de la FPGA) es la misma, Ti=90 šC.
e) Volver a resolver el apartado anterior aÃąadiendo el efecto de la radiaciÃģn tÃĐrmica por ambas caras con una carcasa que estÃĄ a 40 šC, con el modelo de cuerpos negros linealizado.
Como el problema es lineal, todavÃa admite soluciÃģn analÃtica. Integrando el balance energÃĐtico de un elemento dx con conducciÃģn longitudinal y pÃĐrdidas radiativas transversales linealizadas para una Textremo conocida (vale para los dos tramos) y para una Qextremo conocida (para el tercer tramo, aunque en ÃĐl es phi=0):
| > | eqBEdx:=0=k*Ly*Lz*diff(T(x),x,x)+phi*Ly*Lz-2*Ly*h*(T(x)-Tinf);eqTo:=T(0)=Ti;solTi:=dsolve({eqBEdx,T(0)=Ti},T(x));eqQo:=Diff(T,x)[x=(L+LN)/2]=0;solQ0:=dsolve({eqBEdx,D(T)(subs(dat,SI0,(L+LN)/2))=0},T(x)); |
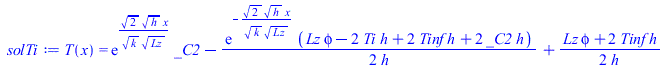 |
![Typesetting:-mprintslash([eqQo := (Diff(T, x))[x = `+`(`*`(`/`(1, 2), `*`(L)), `*`(`/`(1, 2), `*`(LN)))] = 0], [(Diff(T, x))[x = `+`(`*`(`/`(1, 2), `*`(L)), `*`(`/`(1, 2), `*`(LN)))] = 0])](images/p94_59.gif) |
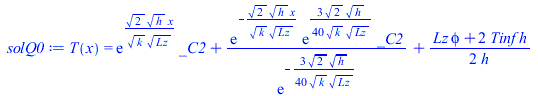 |
donde h es el coeficiente convectivo correspondiente a las pÃĐrdidas radiativas linealizadas, _C2 una constante a obtener por acuerdo en los tramos, y phi la disipaciÃģn volumÃĐtrica (promediada en 'y').
| > | eqh:=h*(T-Tinf)=epsilon*sigma*(T^4-Tinf^4);eqh:=h*(T-Tinf)=4*epsilon*sigma*Tmean^3*(T-Tinf);eqh:=h=4*epsilon*sigma*Tmean^3;Tmean=Ti;Tmean_:=Ti_;h_:=subs(Tmean=Ti_,epsilon=1,dat,rhs(eqh));eqphi:=phi=QN/(LN*Ly*Lz);eqphi_:=subs(Ly=L,dat,%); |
Ahora hay tres tramos, porque el de la derecha tambiÃĐn emite, y hay que imponer las condiciones en los extremos de los tramos. La T(x) en cada tramo es:
| > | T1x:=subs(phi=0,k=k1,_C2=_C21,rhs(solTi));T1x_:=subs(k1=k,eqkeff_alongPCB_,h=h_,dat,SI0,%);T2x:=subs(k=k2,_C2=_C22,rhs(solTi));T2x_:=subs(k2=k,eqkeff_underFPGA_,h=h_,eqphi_,dat,SI0,%);T3x:=subs(phi=0,k=k1,_C2=_C23,rhs(solQ0));T3x_:=evalf(subs(k1=k,eqkeff_alongPCB_,h=h_,dat,SI0,%)); |
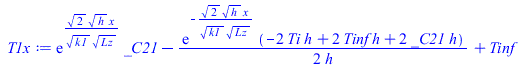 |
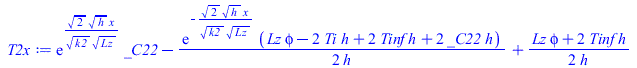 |
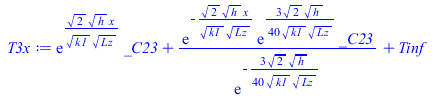 |
y las 4 incÃģgnitas (Ti,C21,C22,C23) se obtienen imponiento las 4 ecuaciones: T1x(-0,025)=Tb, k1·dT1x(0)=k2·dT2x(0), T2x(LN)=T3x(LN), y k2·dT2x(LN)=k3·dT3x(LN), ya que las de T1x(0)=T2x(0)=Ti y dT3x(0,075) ya se han impuesto en la integraciÃģn.
| > | eq1_:=evalf(subs(x=-0.025,dat,SI0,Tb=T1x_));eq2:=k1*A*Diff('T1x',x)[x=0]=k2*A*Diff('T2x',x)[x=0];eq2_:=evalf(subs(x=0,k1=k,eqkeff_alongPCB_,k2=k,eqkeff_underFPGA_,dat,SI0,k1*diff(T1x_,x)=k2*diff(T2x_,x)));eq3:='T2x'[x=LN]='T3x'[x=LN];eq3_:=evalf(subs(x=LN,dat,SI0,T2x_=T3x_));eq4:=k2*A*Diff('T2x',x)[x=LN]=k1*A*Diff('T3x',x)[x=LN];eq4_:=evalf(subs(x=LN,k1=k,eqkeff_alongPCB_,k2=k,eqkeff_underFPGA_,dat,SI0,k2*diff(T2x_,x)=k1*diff(T3x_,x)));sol_:=solve({eq1_,eq2_,eq3_,eq4_},{Ti,_C21,_C22,_C23});T_:=subs(sol_,piecewise(x<0,T1x_,x>0.05,T3x_,T2x_));plot(T_-To,x=-0.025..0.075,T_C=30..70);Ti_:=subs(sol_,Ti)*K_;'Ti_'=TKC(%);Ti2:='T2x'[x=LN];Ti2_:=evalf(subs(sol_,x=LN,dat,SI0,T2x_))*K_;'Ti2_'=TKC(%);Tend:='T3x'[x=(L+LN)/2];Tend_:=evalf(subs(sol_,x=(L+LN)/2,dat,SI0,T3x_))*K_;'Tend_'=TKC(%);N:=40:Tmax:=max(seq(evalf(subs(x=L*i/N,dat,SI0,T_)),i=1..N))*K_;'Tmax'=TKC(%); |
 |
 |
i.e. contando la radiaciÃģn (linealizada) vemos que la Tmax baja de los 112 šC antes calulado a unos 70 šC. TambiÃĐn se ve que el tramo 3 emite calor y por eso se va enfriando desde la fuente (el IC) hacia el borde adiabÃĄtico. Las pendientes en los empalmes no son continuas, pero el flujo de calor sà (Q=kAdT/dx).
f) Resolver numÃĐricamente el apartado anterior.
Lo vamos a hacer en rÃĐgimen transitorio desde un estado inicial con T(x)=Tb, aunque este no sea de equilibrio si Tinf<>Tb, pero es irrelevante para llegar al estacionario..
SoluciÃģn numÃĐrica. Sea N el nÚmero de tramos en que dividimos la chapa completa (N+1 puntos): 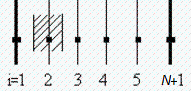 . Desde i=1 hasta i=N/3+1 estÃĄ soleado y el resto no.
. Desde i=1 hasta i=N/3+1 estÃĄ soleado y el resto no.
El balance energÃĐtico de un elemento discreto es:
| > | eqBE:=rho[i]*c[i]*A*Dx*(T[j+1,i]-T[j,i])/Dt=k[i+1]*A*(T[j,i+1]-T[j,i])/Dx-k[i-1]*A*(T[j,i]-T[j,i-1])/Dx+phi[i]*A*Dx-p*h*Dx*(T[j,i]-Tinf);eqTi:=T[j+1,i]=T[j,i]+(Dt/(rho[i]*c[i]))*((k[i+1]*(T[j,i+1]-T[j,i])-k[i-1]*(T[j,i]-T[j,i-1]))/Dx^2+phi[i]-(p*h/A)*(T[j,i]-Tinf));eqT1:=T[j+1,1]=Tb;eqTN1:=T[j+1,N+1]=T[j,N]; |
![Typesetting:-mprintslash([eqTi := T[`+`(j, 1), i] = `+`(T[j, i], `/`(`*`(Dt, `*`(`+`(`/`(`*`(`+`(`*`(k[`+`(i, 1)], `*`(`+`(T[j, `+`(i, 1)], `-`(T[j, i])))), `-`(`*`(k[`+`(i, `-`(1))], `*`(`+`(T[j, i],...](images/p94_97.gif) |
Como hay discontinuidades (en phi, en k, y en rho·c), si no se suaviza habrÃa que tomar una discretizaciÃģn fina.
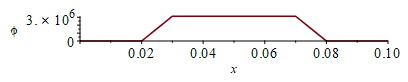
| > | N:=20;Dx:=evalf(subs(dat,SI0,L/N));phi:='phi':phi__:=subs(SI0,rhs(eqphi_)):for i from 1 to N+1 do phi[i]:=0;od:for i from N/4+2 to 3*N/4 do phi[i]:=phi__:od:phi[N/4+1]:=phi__/2:phi[3*N/4+1]:=phi__/2:plot([seq([(i-1)*Dx,phi[i]],i=1..N+1)],x=0..0.1,'phi'=0..phi__);k1__:=subs(SI0,rhs(eqkeff_alongPCB_));k2__:=subs(SI0,rhs(eqkeff_underFPGA_));for i from 1 to N+1 do k[i]:=k1__;od:for i from N/4+2 to 3*N/4 do k[i]:=k2__:od:k[N/4+1]:=(k1__+k2__)/2:k[3*N/4+1]:=%:plot([seq([(i-1)*Dx,k[i]],i=1..N+1)],x=0..0.1,'k'=0..k2__);i:='i':eqrc:=rho*c=Sum(rho[i]*c[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqrc1:=rho*c=(rhoC*cC*LzC+rhoF*cF*LzF+rhoC*cC*f*LzC)/Lz;rhoc1:=subs(dat,SI0,(subs(datC,rho*c*LzC*(1+f))+subs(datF,rho*c*LzF))/Lz);eqrc2:=rho*c=(rhoC*cC*LzC+rhoF*cF*LzF+rhoC*cC*f*LzC+rhoN*cN*LzN)/Lz;rhoc2:=subs(dat,SI0,(subs(datC,rho*c*LzC*(1+f))+subs(datF,rho*c*LzF)+subs(datN,rho*c*LzN))/Lz);'rhoc2_=(rhoc1+rhoc2)/2';rhoc2_:=(rhoc1+rhoc2)/2;for i from 1 to N+1 do rc[i]:=rhoc1;od:for i from N/4+2 to 3*N/4 do rc[i]:=rhoc2_:od:rc[N/4+1]:=(rhoc1+rhoc2_)/2:rc[3*N/4+1]:=%:plot([seq([(i-1)*Dx,rc[i]],i=1..N+1)],x=0..0.1,'rc'=0..rhoc2); |
 |
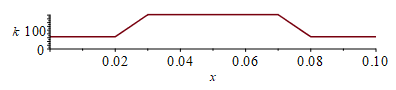 |
![Typesetting:-mprintslash([eqrc := `*`(rho, `*`(c)) = `/`(`*`(Sum(`*`(rho[i], `*`(c[i], `*`(f[i], `*`(delta[i])))), i)), `*`(Sum(delta[i], i)))], [`*`(rho, `*`(c)) = `/`(`*`(Sum(`*`(rho[i], `*`(c[i], `...](images/p94_106.gif) |
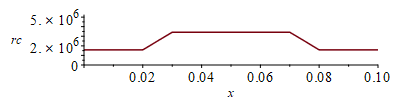 |
donde ya se ha tenido en cuenta para el producto rho·c (rc=rho·c), al igual que para la conductividad k, que la FPGA sÃģlo cubre la mitad de la profundidad en y,
La discretizaciÃģn temporal es (Note: to simulate case d (h=0) use tsim=750 s and M=3500).
| > | T:='T':tsim:=300;M:=1500;Dt:=evalf(tsim/M);Fo_:=k1__*Dt/(rhoc1*Dx^2);Lz_:=subs(dat,SI0,Lz);h_:=subs(SI0,h_);Tinf_:=subs(dat,SI0,Tinf);T0_:=subs(dat,SI0,Tb);T:=Matrix(1..M+1,1..N+1,T0_): |
Y la simulaciÃģn espacio-temporal:
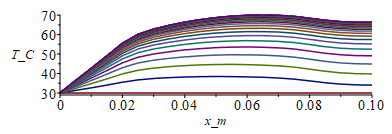
| > | for j from 1 to M do T[j+1,1]:=T0_;T[j+1,N+1]:=T[j,N];for i from 2 to N do T[j+1,i]:=T[j,i]+(Dt/(rc[i]))*(((k[i+1]+k[i])*(T[j,i+1]-T[j,i])-(k[i]+k[i-1])*(T[j,i]-T[j,i-1]))/(2*Dx^2)+phi[i]-(2/Lz_)*h_*(T[j,i]-Tinf_));od:od:i:='i':j:='j':Mjump:=50:sx:=seq([seq([i*Dx-Dx,T[1+j_*Mjump,i]-To],i=1..N+1)],j_=0..M/Mjump):plot([sx],x_m=0..0.1,T_C=30..70);st:=seq([seq([j*Dt,T[j,i]-To],j=1..M+1)],i=1..N+1):plot([st],t_s=0..tsim,T_C=30..70);Tmax:=max(max(T))*K_;'Tmax'=TKC(%);
|
 |
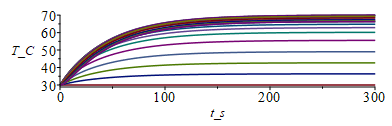 |
Vemos que la T(x) final coincide con la del modelo analÃtico, y que se tarda 2 o 3 minutos en alcanzar prÃĄcticamente el rÃĐgimen estacionario.
Puede repetirse la simulaciÃģn numÃĐrica sin linealizar la radiaciÃģn, i.e. substituyendo h·(T-Tinf) por sigma·(T^4-Tinf^4), obteniÃĐndose un perfil T(x) similar (la Tmax aumentarÃa de 70 šC a 74 šC).
g) Resolver el caso bidimensional estacionario.
Se ha resuelto en Matlab y el resultado es:
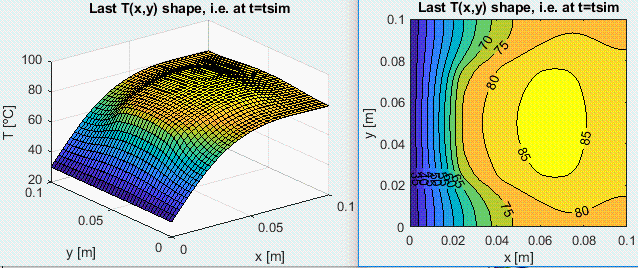
Como era de esperar, al estar mÃĄs concentrada la disipaciÃģn, la Tmax aumenta bastante, de 70 šC a 87 šC, por lo que el modelo 1D no es muy bueno.
Si nos fijamos en el perfil de temperaturas en los bordes aislados, e.g. en T(x,y=0), podrÃa parecer errÃģneo que el modelo 1D no sirva de aproximaciÃģn al modelo 2D (la Tmax era 70 šC en el 1D y vale 80 šC en el 2D), i.e. la T en el borde es mayor cuanto mÃĄs alejada del borde estÃĄ la disipaciÃģn. La explicaciÃģn es que, manteniendo fija la disipaciÃģn total (10 W), cuanto mÃĄs concentrada estÃĐ mÃĄs subirÃĄ la T en la FPGA, y como hacia los lados laterales fluye poco calor (los bordes son adiabÃĄticos), toda la tarjeta PCB a una cierta cota x aumenta su temperatura, no solo la parte bajo la FPGA.
| > |