Considûˋrese una tarjeta electrû°nica (PCB) de 100ÿÇ100ÿÇ1,5 mm3 de FR-4, con recubrimientos de 50 ÿÙm de cobre por cada lado, que en una de las caras es continuo, y en la otra sû°lo ocupa el 10% de la superficie, en la cual van montados diversos componentes electrû°nicos que en funcionamiento normal disipan 3 W en total, y cuya capacidad tûˋrmica se estima en 200 J/K. La tarjeta va insertada en una placa base por uno de los bordes, el cual se va a considerar permanentemente a 25 ô¤C, pudiendo considerarse los otros tres bordes aislados. Se pide:
a) Determinar la conductividad tûˋrmica efectiva, y la distribuciû°n de temperatura en la placa suponiendo la disipaciû°n uniformemente distribuida. ô¢Y sin el recubrimiento de cobre de la cara posterior?
b) Estimar la diferencia de temperatura entre las dos caras de la tarjeta en el caso anterior.
c) Temperatura mûÀxima considerando que ademûÀs se transmite calor por radiaciû°n, con una emisividad media de 0,8 por el lado de los componentes, y de 0,3 por la cara opuesta, con una caja electrû°nica que se puede suponer negra y a 40 ô¤C. ô¢Quûˋ influencia tendrûÙa aûÝadir el efecto de la convecciû°n con aire encerrado, suponiendo un coeficiente de 2 W/(m2ôñK)?
d) Evoluciû°n espacio-temporal de la temperatura si se considera un funcionamiento periû°dico en el que, durante 10 minutos de cada 90 minutos, la tarjeta consume el doble de potencia.
e) Repetir los apartados anteriores suponiendo ahora que los componentes que mûÀs disipan estûÀn en un ûÀrea central de 60û60 mm2.
Data:
| > |
read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):interface(rtablesize=infinity): |
| > |
su1:="FR4":su2:="Cobre":dat:=[Lx=0.1*m_,Ly=0.1*m_,Lz=1.5e-3*m_,Lcu=50e-6*m_,f=0.1,Wst=3*W_,C=200*J_/K_,Tb=(25+273.15)*K_,T0=(40+273.15)*K_,epsilon1=0.8,epsilon2=0.3,h12=2*W_/(m_^2*K_),Ls=0.02*m_]; |
Eqs. const. (F=FR-4, C=Cobre):
| > |
datF:=rho=1850*kg_/m_^3,c=700*J_/(kg_*K_),k=0.5*W_/(m_*K_),kt=0.25*W_/(m_*K_);datC:=get_sol_data(su2);dat:=op(dat),Const,SI2,SI1: |
a) Determinar la conductividad tûˋrmica efectiva, y la distribuciû°n de temperatura en la placa suponiendo la disipaciû°n uniformemente distribuida. ô¢Y sin el recubrimiento de cobre de la cara posterior?
El problema puede considerarse unidimensional porque una dimensiû°n es muy pequeûÝa (1,5 frente a 100), y el calor va a fluir hacia el borde anclado (en las otras direcciones estûÀ aislado).
| > |
eqkeff:=k=Sum(k[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqkeff:=k=(kC*f*Lcu+kF*(Lz-2*Lcu)+kC*Lcu)/Lz;eqkeff_:=k=subs(kC=k,datC,kF=k,datF,dat,rhs(%)); |
Sin el recubrimiento de cobre de la cara posterior, serûÙa:
| > |
eqkeff_wo:=k=(kC*f*Lcu+kF*(Lz-2*Lcu))/Lz;eqkeff_wo_:=k=subs(kC=k,datC,kF=k,datF,dat,rhs(%)); |
 |
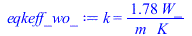 |
(2) |
El perfil de temperatura en la placa, T(x), debido a una disipaciû°n uniforme, de densidad volumûˋtrica phi=Wdis/V, es:
| > |
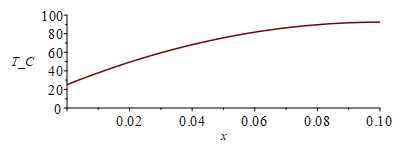
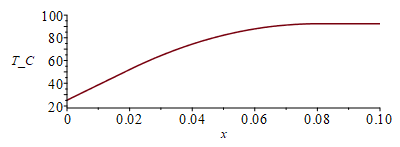
eqphi:=phi=Wdis/V;eqphi:=phi=Wst/(Lx*Ly*Lz);eqphi_:=phi=subs(dat,SI0,rhs(%))*W_/m_^3;eqBElocal:=rho*Ly*Lz*dx*c*diff(T(x,t),t)=Wst*dx/Lx+k*Ly*Lz*dx*diff(T(x,t),x,x);eqBElocal_:=0=phi+k*diff(T(x),x,x);eqT:=T=A*x+B-(phi/(2*k))*x^2;eqBC0:=Tb=B;eqBC1:=Tmax=subs(x=Lx,rhs(eqT));eqB0p:=k*Ly*Lz*dT/dx[x=0]=Wst;eqB0p:=k*Ly*Lz*A=Wst;eqT_:=T=Tb+x*Wst/(k*Ly*Lz)-x^2*Wst/(2*k*Lx*Ly*Lz);Tmax_:=subs(x=Lx,eqkeff_,dat,rhs(eqT_));Tmax:=TKC(%);plot(subs(eqkeff_,dat,SI0,rhs(eqT_)-273),x=0..subs(dat,SI0,Lx),T_C=0..100);Tmax_sin_:=subs(x=Lx,eqkeff_wo_,dat,rhs(eqT_));'Tmax_sin_'=TKC(%);eqTc:=eqT:eqTc_:=eqT_: |
i.e. la temperatura mûÀxima se alcanzarûÀ en el extremo opuesto al anclaje, y serûÀ Tmax=92 ô¤C, que es inferior al valor mûÀximo de trabajo recomendado para el FR-4, aunque podrûÙa daûÝar algû¤n componente.
Sin le disipador de cobre de la cara trasera, la resina de la FR-4 se chamuscarûÙa, desprendiendo gases tû°xicos, y toda la placa se estropearûÙa enseguida (el valor de 588 ô¤C nunca se alcanzarûÙa).
b) Estimar la diferencia de temperatura entre las dos caras de la tarjeta en el caso anterior.
Para comprobar que la diferencia de temperatura de una cara a otra de la PCB es insignificante, podemos comparar las resistencias tûˋrmicas.
| > |
eqQ:=k*A*DT/L=DT/R;eqRparal:=R=Leff/(keff*A);Leff=Lx/2;eqkeff_;eqA:=A=Ly*Lz;eqRparal:=R=subs(eqkeff_,dat,SI0,(Lx/2)/(k*Ly*Lz))*K_/W_;eqRperp:=R=Rcu1+RF+Rcu2;eqRperp:=R=RF;eqRperp:=R=(Lz-2*Lcu)/(kFt*Lx*Ly);eqRperp_:=R=subs(kFt=kt,A=Ly*Lz,datF,dat,SI0,rhs(%))*K_/W_;DTt:=Wst*R;DTt_:=subs(dat,eqRperp_,SI0,%)*K_; |
efectivamente, la resistencia tûˋrmica al travûˋs, Rperp=0,56 K/W, es mucho menor que a lo largo, Rparal=22 K/W. Por cierto, que estos valores sirven para estimar las diferencias de temperatura: para que fluya Q=3 W longitudinalmente hacia el anclaje hace falta un salto de DT=QR=3ôñ22,4=67 K (compûÀrese con el valor obtenido: 92-25=67 K), mientras que para que fluya Q=3 W perpendicularmente a travûˋs del PCB hace falta un salto de DT=QR=3ôñ0,56=1,7 K, que es el valor despreciado en el modelo 1D.
b) Temperatura mûÀxima considerando que ademûÀs se transmite calor por radiaciû°n, con una emisividad media de 0,8 por el lado de los componentes, y de 0,3 por la cara opuesta, con una caja electrû°nica que se puede suponer negra y a 40 ô¤C. ô¢Quûˋ influencia tendrûÙa aûÝadir el efecto de la convecciû°n con aire encerrado, suponiendo un coeficiente de 2 W/(m2ôñK)?
Hay que aûÝadir unos sumideros distribuidos para modelar las pûˋrdidas al ambiente, que no serûÀn uniformes porque dependen de la temperatura local. Si sû°lo se aûÝadiese la convecciû°n, el problema seguirûÙa siendo lineal y con soluciû°n analûÙtica, pero con la radiaciû°n hay que resolverlo numûˋricamente. Resolveremos el transitorio (problema parabû°lico), que es mûÀs sencillo que directamente el estacionario (problema elûÙptico). Vamos a poner ya la capacidad tûˋrmica de los componentes electrû°nicos, dejando las demûÀs dimensiones anteriores, aunque para el rûˋgimen estacionario da igual.
Suponemos que los componentes electrû°nicos no contribuyen a la conducciû°n de calor en la direcciû°n paralela a la tarjeta, por estar dispersos (en los circuitos de cobre sûÙ hemos tenido en cuenta la continuidad).
Tomaremos un valor inicial de temperatura de la placa igual a la del encastre,Tb=25 ô¤C.
| > |
eq11_24_0_;eq11_24_gen_;T:='T':eqp:=p=2*Ly;eqeps:=epsilon[lat]=(epsilon1+epsilon2)/2;eqh:=h[lat]=0;eq0:=subs(eqp,eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_0_);eqi:=subs(eqp,eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_gen_);eqN:=T[N,j+1]=T[N-1,j+1]; |
| > |
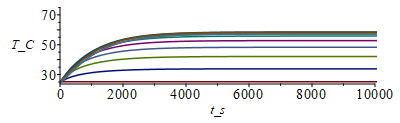
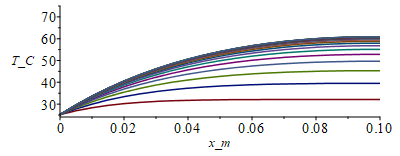
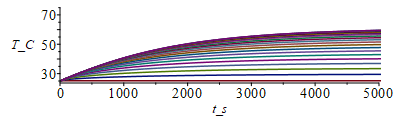
N:=20;M:=1000;T0:=subs(dat,SI0,T0);Tb:=subs(dat,SI0,Tb);Dx:=subs(dat,SI0,Lx)/N;Dt:=10;phi:=subs(SI0,rhs(eqphi_));eqrho_eff:=rho[eff]=rhoF;rho:=subs(datF,SI0,rho);eqc_eff:=c[eff]=C/(rhoF*Lx*Ly*Lz)+(rhoC*cC*f*Lcu+rhoF*cF*(Lz-2*Lcu)+rhoC*cC*Lcu)/(rhoF*Lz);c:=subs(cC=c,rhoC=rho,datC,rhoF=rho,cF=c,datF,dat,SI0,rhs(%));Lz:=subs(dat,SI0,Lz);Ly:=subs(dat,SI0,Ly);p:=subs(dat,SI0,2*Ly);h:=0;sigma:=subs(dat,SI0,sigma);epsilon:=subs(dat,epsilon1+epsilon2)/2;eqa:=a='k/(rho*c)';eqa_:=subs(eqkeff_,dat,SI0,eqa):%*1e6;t_relaj:=Lx^2/a;t_relaj_:=subs(eqa_,dat,SI0,%)*s_;eqFo:=Fo='k*Dt/(rho*c*Dx^2)';Fo:=subs(eqkeff_,dat,SI0,rhs(eqFo));T:=Matrix(1..M,1..N+1,Tb):for j from 1 to M-1 do T[j+1,1]:=Tb:for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+phi*Dt/(rho*c)-(p*Dt/(rho*c*Lz*Ly))*(h*(T[j,i]-T0)+epsilon*sigma*(T[j,i]^4-T0^4));od: T[j+1,N+1]:=T[j+1,N];od:Tmax:=max(T)*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([i*Dx-Dx,T[j*50-9,i]-273],i=1..N+1)],j=1..M/50):plot([sx],x_m=0..0.1,T_C=25..75);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..5000,T_C=25..75); |
i.e. la Tmax es ahora de 61 ô¤C, aceptable en general (sin radiaciû°n era un poco alta, 92 ô¤C). El tiempo de relajaciû°n por conducciû°n era de unos 10 000 s, pero con radiaciû°n es menor.
Si se aûÝade la convecciû°n:
| > |
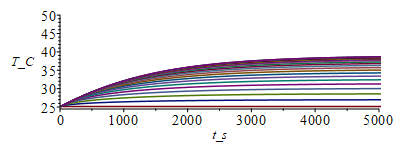
T:='T':Fo:='Fo':phi:='phi':Dt:='Dt':rho:='rho':;c:='c':sigma:='sigma':h:='h':eqh:=h[lat]=h;q0:=subs(eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_0_);eqi:=subs(eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_gen_);eqN:=T[N,j+1]=T[N-1,j+1];N:=20;M:=1000;T0:=subs(dat,SI0,T0);Tb:=subs(dat,SI0,Tb);Dx:=subs(dat,SI0,Lx)/N;Dt:=10;phi:=subs(SI0,rhs(eqphi_));eqrho_eff:=rho[eff]=rhoF;rho:=subs(datF,SI0,rho);eqc_eff:=c[eff]=C/(rhoF*Lx*Ly*Lz)+(rhoC*cC*f*Lcu+rhoF*cF*(Lz-2*Lcu)+rhoC*cC*Lcu)/(rhoF*Lz):c:=subs(cC=c,rhoC=rho,datC,rhoF=rho,cF=c,datF,dat,SI0,rhs(%));h:=subs(dat,SI0,h12);sigma:=subs(dat,SI0,sigma);epsilon:=subs(dat,epsilon1+epsilon2)/2;eqFo:=Fo='k*Dt/(rho*c*Dx^2)';Fo:=subs(eqkeff_,dat,SI0,rhs(eqFo));T:=Matrix(1..M,1..N+1,Tb):for j from 1 to M-1 do T[j+1,1]:=Tb;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+phi*Dt/(rho*c)-(p*Dt/(rho*c*Lz*Ly))*(h*(T[j,i]-T0)+epsilon*sigma*(T[j,i]^4-T0^4));od: T[j+1,N+1]:=T[j+1,N];od:Tmax:=max(T)*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([(i-1)*Dx,T[j*50,i]-273],i=1..N+1)],j=1..M/50):plot([sx],x_m=0..0.1,T_C=25..50);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..5000,T_C=25..50); |
i.e. con convecciû°n bajarûÙa la Tmax de 61 ô¤C a 39 ô¤C.
d) Evoluciû°n espacio-temporal de la temperatura si se considera un funcionamiento periû°dico en el que, durante 10 minutos de cada 90 minutos, la tarjeta consume el doble de potencia.
Ahora la funciû°n de disipaciû°n varûÙa con el tiempo. Como hemos visto que el transitorio es del orden de 5000 s (90 min), cuando empiece a disipar el doble (a los 80 min) ya casi habrûÀ perdido la memoria, y en los 10 min de alta disipaciû°n apenas se calentarûÀ un poco mûÀs, y luego tardarûÀ un rato en volver al valor base. Tomaremos un periodo de simulaciû°n de 3ôñ90=270 min (16200 s) para ver cû°mo evoluciona. Ya no consideramos la convecciû°n.
| > |
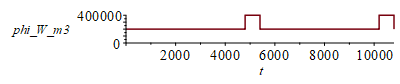
phi:='phi':eqphi_t:=phi(t)=subs(SI0,rhs(eqphi_))*piecewise(t>80*60 and t<90*60,2,t>170*60 and t<180*60,2,1);plot(rhs(%),t=0..180*60,phi_W_m3=0..400000) |
| > |
T:='T':Fo:='Fo':phi:='phi':Dt:='Dt':rho:='rho':c:='c':sigma:='sigma':h:='h':eqh:=h[lat]=0;q0:=subs(phi=phi[j],eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_0_);eqi:=subs(phi=phi[j],eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_gen_);N:=20;M:=1620;T0:=subs(dat,SI0,T0);Tb:=subs(dat,SI0,Tb);Dx:=subs(dat,SI0,Lx)/N;Dt:=10;eqrho_eff:=rho[eff]=rhoF:rho:=subs(datF,SI0,rho):eqc_eff:=c[eff]=C/(rhoF*Lx*Ly*Lz)+(rhoC*cC*f*Lcu+rhoF*cF*(Lz-2*Lcu)+rhoC*cC*Lcu)/(rhoF*Lz):c:=subs(cC=c,rhoC=rho,datC,rhoF=rho,cF=c,datF,dat,SI0,rhs(%)):h:=0;sigma:=subs(dat,SI0,sigma);epsilon:=subs(dat,epsilon1+epsilon2)/2;eqFo:=Fo='k*Dt/(rho*c*Dx^2)';Fo:=subs(eqkeff_,dat,SI0,rhs(eqFo)); |
| > |
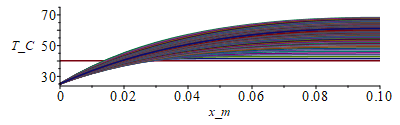
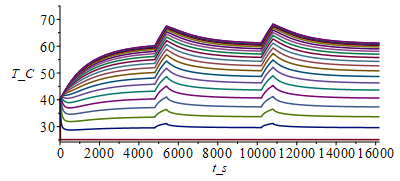
T:=Matrix(1..M,1..N+1,T0):for j from 1 to M-1 do T[j+1,1]:=Tb;for i from 2 to N do phi_:=evalf(subs(t=j*Dt,rhs(eqphi_t)));T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+phi_*Dt/(rho*c)-(p*Dt/(rho*c*Lz*Ly))*(h*(T[j,i]-T0)+epsilon*sigma*(T[j,i]^4-T0^4));od: T[j+1,N+1]:=T[j+1,N];od:Tmax:=max(T)*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([(i-1)*Dx,T[j*10-9,i]-273],i=1..N+1)],j=1..M/10):plot([sx],x_m=0..0.1,T_C=25..75);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..16200,T_C=25..75); |
Vemos que despuûˋs del transitorio inicial (los 5000 s primeros), la respuesta es prûÀcticamente periû°dica, subiendo la temperatura mûÀxima de 61 ô¤C a 67 ô¤C durante los 10 minutos que disipa el doble (porque en tan poco rato no le da tiempo a calentarse mûÀs). La superposiciû°n de perfiles T(x) para diversos tiempos no es muy ilustrativa porque montan unos sobre otros.
e) Repetir los apartados anteriores suponiendo ahora que los componentes que mûÀs disipan estûÀn en un ûÀrea central de 60û60 mm2.
TodavûÙa podemos aproximar con el modelo 1D porque las zonas laterales no son muy extensas y estûÀn aisladas en sus bordes exteriores.
Sû°lo conducciû°n 1D (sin radiaciû°n).
| > |
Tb:='Tb':Tp:=piecewise(x<=Ls,Tb+a0*x,x>Lx-Ls,Tm,a1+a2*x+a3*x^2);dat:=[Lx=0.1*m_,Ly=0.1*m_,Lz=1.5e-3*m_,Lcu=50e-6*m_,f=0.1,Wst=3*W_,C=200*J_/K_,Tb=(25+273.15)*K_,T0=(40+273.15)*K_,epsilon1=0.8,epsilon2=0.3,h12=2*W_/(m_^2*K_),Ls=0.02*m_]: |
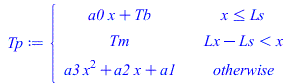 |
(7) |
LûÙmite analûÙtico a trozos.
| > |
eqTbprime:=k*A*diff(Tb+a0*x,x)=Wst;eqTi:=subs(x=Ls,Tb+a0*x=a1+a2*x+a3*x^2);eqTiprime:=subs(x=Ls,diff(Tb+a0*x,x)=diff(a1+a2*x+a3*x^2,x));eqTm:=subs(x=Lx-Ls,a1+a2*x+a3*x^2)=Tm;eqTmprime:=subs(x=Lx-Ls,diff(a1+a2*x+a3*x^2,x)=0);sol:=solve({eqTbprime,eqTi,eqTiprime,eqTm,eqTmprime},{a0,a1,a2,a3,Tm});sol_:=subs(eqkeff_,eqA,dat,SI0,sol);Tm=TKC(subs(sol_,Tm*K_));plot(subs(sol_,dat,SI0,Tp)-273,x=0..subs(dat,SI0,Lx),T_C=20..100); |
vemos que la Tmax es la misma, 92 ô¤C. Transitorio numûˋrico:
| > |
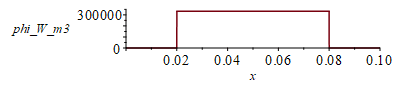
T:='T':T0:='T0':Fo:='Fo':p:='p':phi:='phi':Dt:='Dt':Dx:='Dx':rho:='rho':c:='c':C:='C':sigma:='sigma':epsilon:='epsilon':h:='h':Ly:='Ly':Lz:='Lz':Tb:='Tb':c:='c':T:='T':eqphi_x:=phi(x)=subs(dat,SI0,rhs(eqphi_)*Lx/(Lx-2*Ls)*piecewise(x<Ls,0,x>Lx-Ls,0,1));plot(rhs(%),x=0..0.1,phi_W_m3=0..350000);eq11_24_0_;eq11_24_gen_;T:='T':eqp:=p=2*Ly;eqeps:=epsilon[lat]=epsilon1+epsilon2;eqh:=h[lat]=0;eq0:=subs(phi=phi[0],eqp,eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_0_);eqi:=subs(phi=phi[i],eqp,eqeps,E0=0,h0=0,eqh,epsilon0=0,eq11_24_gen_);eqN:=T[N,j+1]=T[N-1,j+1];dat:=[Lx=0.1*m_,Ly=0.1*m_,Lz=1.5e-3*m_,Lcu=50e-6*m_,f=0.1,Wst=3*W_,C=200*J_/K_,Tb=(25+273.15)*K_,T0=(40+273.15)*K_,epsilon1=0.8,epsilon2=0.3,h12=2*W_/(m_^2*K_),Ls=0.02*m_]: |
| > |
N:=10;M:=1000;T0:=subs(dat,SI0,T0);Tb:=subs(dat,SI0,Tb);Dx:=subs(dat,SI0,Lx)/N;Dt:=20;eqrho_eff:=rho[eff]=rhoF;rho:=subs(datF,SI0,rho);Lz:=subs(dat,SI0,Lz);Ly:=subs(dat,SI0,Ly);eqc_eff:=c[eff]=C/(rhoF*Lx*Ly*Lz)+(rhoC*cC*f*Lcu+rhoF*cF*(Lz-2*Lcu)+rhoC*cC*Lcu)/(rhoF*Lz);c:=subs(cC=c,rhoC=rho,datC,rhoF=rho,cF=c,datF,dat,SI0,rhs(%));p:=subs(dat,SI0,2*Ly);h:=0;sigma:=subs(Const,SI0,sigma);epsilon:=1+0*subs(dat,epsilon1+epsilon2)/2;eqFo:=Fo='k*Dt/(rho*c*Dx^2)';Fo:=subs(eqkeff_,dat,SI0,rhs(eqFo));T:=Matrix(1..M,1..N+1,Tb): |
| > |
for j from 1 to M-1 do T[j+1,1]:=Tb;for i from 2 to N do phi_:=evalf(subs(x=(i-1)*Dx,rhs(eqphi_x)));T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+phi_*Dt/(rho*c)-(p*Dt/(rho*c*Lz*Ly))*(h*(T[j,i]-T0)+epsilon*sigma*(T[j,i]^4-T0^4));od: T[j+1,N+1]:=T[j+1,N];od:Tmax:=max(T)*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([[0,Tb-273.15],seq([(i-1)*Dx,T[j*10-9,i]-273],i=1..N+1)],j=1..M/10):plot([sx],x_m=0..0.1,T_C=25..75);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..10000,T_C=25..75); |
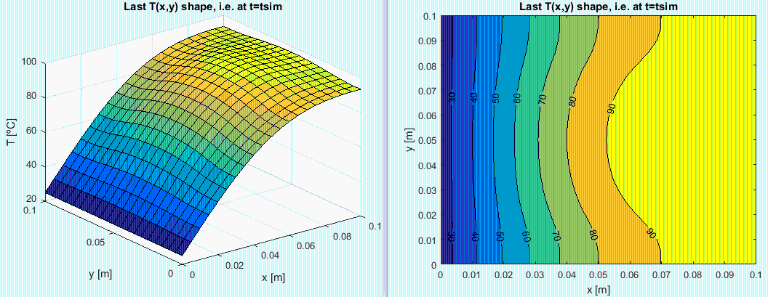
Para comprobar la bondad del modelo 1D, se muestra el resultado de la simulaciû°n en 2D con Matlab.
![k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delta[i], i)))](images/p83_5.gif)
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(p, `*`(Dt, `*`(`+`(`*`(h[lat],...](images/p83_39.gif)
![T[0, `+`(j, 1)] = `+`(T[0, j], `*`(2, `*`(Fo, `*`(`+`(T[1, j], `-`(T[0, j]))))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(2, `*`(Ly, `*`(Dt, `*`(`+`(`*`(`/`(1, 2), `*`(epsilon1)), `*`(`/`...](images/p83_43.gif)
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(2, `*`(Ly, `*`(Dt, `*`(`+`(`*`...](images/p83_44.gif)
![T[0, `+`(j, 1)] = `+`(T[0, j], `*`(2, `*`(Fo, `*`(`+`(T[1, j], `-`(T[0, j]))))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(.2, `*`(Dt, `*`(`+`(`*`(h, `*`(`+`(T[0, j], `-`(T[infinity])))), ...](images/p83_74.gif)
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(.2, `*`(Dt, `*`(`+`(`*`(h, `*`...](images/p83_75.gif)

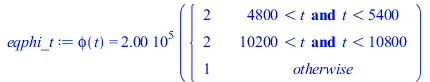
![T[0, `+`(j, 1)] = `+`(T[0, j], `*`(2, `*`(Fo, `*`(`+`(T[1, j], `-`(T[0, j]))))), `/`(`*`(phi[j], `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(.2, `*`(Dt, `*`(`+`(`*`(`/`(1, 2), `*`(epsilon1)), `*`(`/`(1, ...](images/p83_99.gif)
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `/`(`*`(phi[j], `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(.2, `*`(Dt, `*`(`+`(`*`(`/`...](images/p83_100.gif)
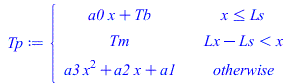
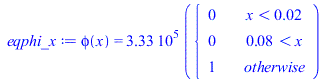
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(p, `*`(Dt, `*`(`+`(`*`(h[lat],...](images/p83_129.gif)