>	restart:#"m11_p79"

11.79. Se saca de un baño de agua y hielo una esfera de 50 mm de diámetro de acero inoxidable y se sumerge en agua hirviendo con una coeficiente convectivo que se estima en 4 kW/m2. Se pide:

a) Resolver la ecuación del calor por separación de variables, suponiendo que la temperatura superficial es constante.

b) Resolver la ecuación del calor por separación de variables para el valor dado del coeficiente conductivo.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Acero_inox":dat:=[D=0.05*m_,T0=273*K_,T1=373*K_,h=4000*W_/(m_^2*K_)];assume(r>=0,b>0,n,integer,N,integer):

Eqs. const.:

>	Sdat:=get_sol_data(su):dat:=op(dat),Sdat,a=subs(Sdat,k/(rho*c)),R=subs(dat,D/2),Const,SI2,SI1:k=subs(dat,k);a=subs(dat,SI0,a)*1e6*mm_^2/s_;

a) Resolver la ecuación del calor por separación de variables, suponiendo que la temperatura superficial es constante.

Llamando DT=T(r)-T0, DT1=T1-T0, la ecuación del calor en esféricas y las condiciones iniciales y de contorno son:

>	eqHT:=diff(DT(r,t),t)/a=(1/r^2)*diff(r^2*diff(DT(r,t),r),r);eqIC:=DT(r,t)[t=0]=0;eqBC0:=Diff(DT(r,t),r)[r=0]=0;eqBC1:=DT(r,t)[r=R]=DT1;

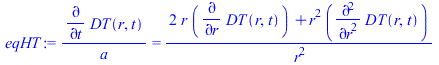Resolviendo por separación de variables:

>

sepvar:=DT(r,t)=Rr(r)*T(t);eqHT_:=expand(eval(subs(sepvar,n=2,eqHT/DT(r,t))));deqT:=lhs(eqHT_)=-b^2;eqT:=dsolve({deqT,T(0)=1},T(t));deqR:=rhs(eqHT_)=-b^2;eqR:=dsolve({deqR,subs(r=0,diff(Rr,r))=0,Rr(R)=DT1},Rr(r));eqR:=Rr(r)=R*sin(bn*r)/r;eqDTn:=DT(r,t)=subs(b=bn,rhs(eqT)*rhs(eqR));eqHT__:=expand(eval(subs(eqDTn,n=2,eqHT)));DTgen:=DT1+subs(b=bn,Sum(cn*rhs(eqR)*rhs(eqT),n=1..N));BC0:=limit(diff(DTgen,r),r=0)=0;BC1:=eval(subs(r=R,DTgen))=DT1;bn:=n*Pi/R;IC:=DT[t=0]=0;IC:=eval(subs(t=0,DTgen))=0;ICn:=cn*rhs(eqR)=0;eqICn:=int(rhs(eqR)*DT1*Pi*r^2,r=0..R)+eval(int(lhs(ICn)*rhs(eqR)*Pi*r^2,r=0..R))=0;cn_:=solve(%,cn);DT:=subs(cn=cn_,DTgen);q:=simplify(eval(subs(r=R,-k*diff(DT,r))));

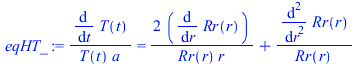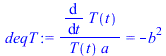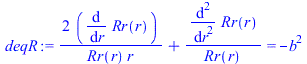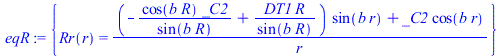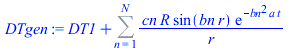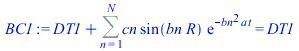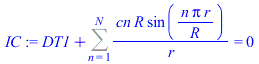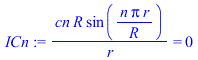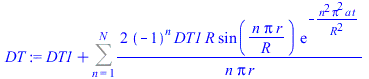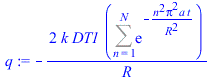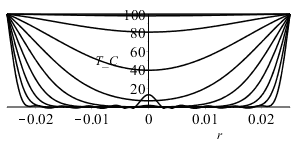
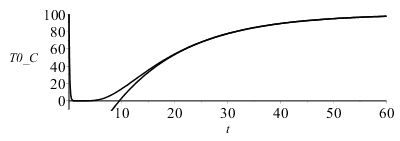
Para ver cuántos términos es preciso retener, representamos las soluciones para N=1 (T_1) y para N=10 (T_10).

>

DT1:=T1-T0;T_1:=evalf(subs(N=1,dat,SI0,DT));T_10:=evalf(subs(N=10,dat,SI0,DT)):plot([seq(subs(t=2^i,T_10),i=-2..7)],r=-subs(dat,SI0,R)..subs(dat,SI0,R),T_C=0..100,color=black);plot(subs(r=1e-6,dat,[T_1,T_10]),t=0..60,T0_C=-10..100,color=black);Q:=simplify(eval(subs(r=R,dat,SI0,k*Pi*D^2*diff(T_1,r)))):Q_:=subs(r=R,dat,SI0,k*Pi*D^2*diff(T_10,r)):plot([Q,Q_],t=0..60,QR_W=0..1500,color=black);T0_30:=evalf(subs(r=1e-6,t=30,dat,SI0,T_10))*`ºC`;QR_30:=evalf(subs(t=30,dat,SI0,Q_))*W_;DEpercent_30:=int(subs(t=30,dat,SI0,T_10*4*Pi*r^2/(Pi*D^3/6)),r=0..subs(dat,SI0,R));

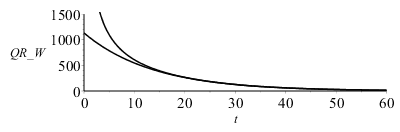con r [m], t [s]. Se observa que solo hay diferencia entre N=1 y N=10 para tiempos cortos (t<10 s); e.g. al cabo de 30 s, la temperatura en el centro ya ha subido desde 0 ºC hasta T0=78 ºC, y el flujo de calor que sale por la superficie es de Q0=127 W, habiendo ganado ya un 93 % de la energía térmica total que ganará (DEtot=m*c*(T2-T1)). Al principio, Q0 tiende a infinito.

La estimación del tiempo de relajación por conducción para una esfera es Dt=(D/6)^2/a=15 s, ya que el tamaño característico es L=V/A=(Pi*D^3/6)/(Pi*D^2)=D/6.

b) Resolver la ecuación del calor por separación de variables para el valor dado del coeficiente conductivo.

La ecuación del calor y las condiciones iniciales no cambian, pero la condición de contorno exterior sí:

>	bn:='bn':DT:='DT':DT1:='DT1':eqHT:=diff(DT(r,t),t)/a=(1/r^2)*diff(r^2*diff(DT(r,t),r),r);eqBC0:=Diff(DT(r,t),r)[r=0]=0;eqBC1:=Diff(DT(r,t),r)[r=R]=h*(DT(R,t)-DT1);eqIC:=DT(r,t)[t=0]=0;

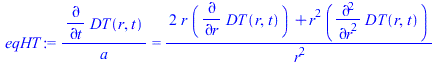	(1)

La separación de variables es como antes:

>

sepvar:=DT(r,t)=Rr(r)*T(t);eqHT_:=expand(eval(subs(sepvar,n=2,eqHT/DT(r,t))));deqT:=lhs(eqHT_)=-b^2;eqT:=dsolve({deqT,T(0)=1},T(t));deqR:=rhs(eqHT_)=-b^2;eqR:=dsolve({deqR,subs(r=0,diff(Rr,r))=0,Rr(R)=DT1},Rr(r));eqR:=Rr(r)=R*sin(bn*r)/r;eqDTn:=DT(r,t)=subs(b=bn,rhs(eqT)*rhs(eqR));eqHT__:=expand(eval(subs(eqDTn,n=2,eqHT)));DTgen:=DT1+subs(b=bn,Sum(cn*rhs(eqR)*rhs(eqT),n=1..N));BC0:=limit(diff(DTgen,r),r=0)=0;BC1:=eval(subs(r=R,-k*diff(DTgen,r)))=h*(subs(r=R,DTgen)-DT1);BC1:=simplify(rhs(%)-lhs(%))=0;eqBC1:=h*R/k+bn*R*cos(bn*R)/sin(bn*R)-1=0;IC:=DT[t=0]=0;IC:=eval(subs(t=0,DTgen))=0;ICn:=cn*rhs(eqR)=0;eqICn:=int(rhs(eqR)*DT1*Pi*r^2,r=0..R)+eval(int(lhs(ICn)*rhs(eqR)*Pi*r^2,r=0..R))=0;cn_:=solve(%,cn);DT:=subs(cn=cn_,DTgen);qR:=eval(simplify(eval(subs(r=R,-k*diff(DT,r))));

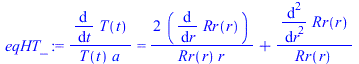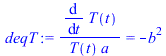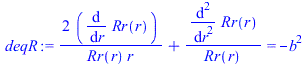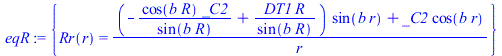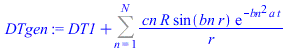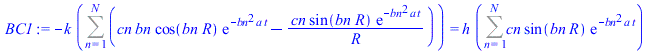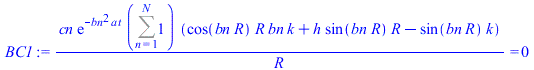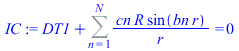Error, `;` unexpected

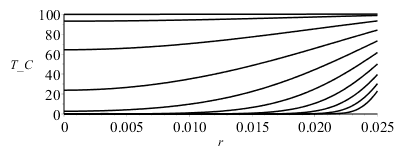
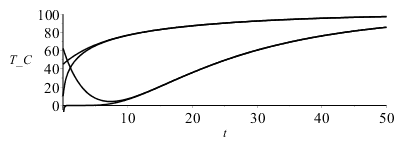
La representación ahora de los perfiles de T(x,t) en varios instantes, de los valores extremos TR(t) y T0(t), y del flujo total de calor en la superficie

>

R_:=subs(dat,SI0,R):DT1:=T1-T0:T_1:=evalf(subs(N=1,dat,SI0,DT));T_10:=evalf(subs(N=10,dat,SI0,DT)):sol__:=subs(dat,SI0,DT1):N_:=10:for i from 0 to N_ do bn_:=fsolve(subs(dat,SI0,eqBC1),bn,i*Pi/R_..i*Pi/R_+Pi/R_);cn__:=(subs(bn=bn_,dat,SI0,cn_));sol__:=sol__+subs(b=bn,bn=bn_,cn=cn__,dat,SI0,cn*rhs(eqR)*rhs(eqT));cat(T_,i):=sol__;od:plot([seq(subs(t=2^i,T_10),i=-2..7)],r=0..R_,T_C=0..100,color=black);plot([subs(r=1e-6,dat,SI0,T_1),subs(r=1e-6,dat,SI0,T_10),subs(r=R,dat,SI0,T_1),subs(r=R,dat,SI0,T_10)],t=0..50,T_C=-5..100,color=black);Q:=simplify(eval(subs(r=R,k*Pi*D^2*diff(T_1,r)))):Q_:=subs(r=R,k*Pi*D^2*diff(T_10,r)):plot(subs(dat,SI0,[Q,Q_]),t=0..50,QR_W_m2=0..3000,color=black);T0_30:=evalf(subs(r=1e-6,t=30,dat,SI0,T_10))*`ºC`;TR_30:=evalf(subs(r=R_,t=30,dat,SI0,T_10))*`ºC`;QR_30:=evalf(subs(t=30,dat,SI0,Q_))*W_;QR_0:=evalf(subs(t=0,dat,SI0,Q_))*W_;DEpercent_30:=int(subs(t=30,dat,SI0,T_10*4*Pi*r^2/(Pi*D^3/6)),r=0..subs(dat,SI0,R));

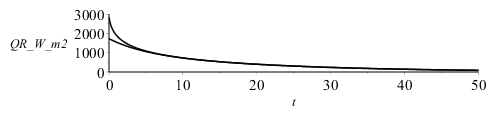Como antes, se observa que solo hay diferencia entre N=1 y N=10 para tiempos cortos (t<10 s); e.g. al cabo de 30 s, la temperatura de la superficie ya ha subido desde 0 ºC hasta TR=92 ºC, la temperatura en el centro desde 0 ºC hasta T0=61 ºC, y el flujo de calor que sale por la superficie todavía es de Q0=238 W (con el modelo de TR fija era de 127 W), habiendo ganado un 82 % de la energía térmica total (antes era un 93 %). El cálculo del flujo de calor en t=0, QR_0=2,8 kW se aproxima bastante al valor teórico h*A*DT=4000*(Pi*0.05^2)*100=3.1 kW

La estimación del tiempo de relajación por convección para una esfera isoterma es Dt=rho*c*(D/6)/h=8 s, que no es adecuada porque esto requiere Bi=hL/k>>1, y aquí es solo Bi=h*(D/6)/k=1,9.

>