| > | restart:#"m11_p78" |
En 1863, W. Thomson (Lord Kelvin) calculó la edad de la Tierra con el siguiente modelo. Supuso la Tierra se formó de una masa de material fundido a unos 2000 K, y que se está enfriando desde su formación. Actualmente la temperatura superficial es de unos 300 K, y el gradiente térmico superficial de unos 25 K/km. La difusividad térmica del suelo es aproximadamente 10-6 m2/s. Se pide:
a) Calcular la edad de la Tierra con ese modelo, suponiendo Tierra plana.
b) Estimar si el modelo de Tierra plana es apropiado.
c) Comparar el flujo de calor geotérmico con el de radiación al espacio exterior, como cuerpo negro.
d) Calcular el flujo de calor geotérmico correspondiente a un modelo del interior de la Tierra consistente en un núcleo de 3500 km de radio de hierro fundido a unos 5000 K (a muy alta presión), y un manto externo cuyas propiedades se asimilan a las de la sílice. Estimar un valor medio de generación interna de energía (desintegración nuclear) que ajuste al valor medido de 0,07 W/m2 del flujo medio en superficie.
e) Calcular el flujo de calor geotérmico correspondiente a un modelo de corteza terrestre de 35 km de espesor, con unos 900 K en la parte inferior. Estimar un valor medio de generación interna de energía (desintegración nuclear) que ajuste al valor medido de 0,07 W/m2 del flujo medio en superficie.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su:="Silice_(cuarzo)":dat:=[Tinf=2000*K_,Ts=300*K_,dTdz0=0.025*K_/m_,aK=1e-6*m_^2/s_,zG=3.5e6*m_,TG=5000*K_,q0=0.07*W_/m_^2,zm=35e3*m_,Tm=900*K_]; |
Eqs. const.:
| > | dat:=op(dat),get_sol_data(su),Const,SI2,SI1:R[Tierra]=subs(dat,R[T]); |
a) Calcular la edad de la Tierra con ese modelo, suponiendo Tierra plana.
Se trataría de un problema de conducción de calor unidimensional en un medio plano semiinfinito (pensando que no ha habido tiempo para que el enfriamiento llegue hasta el centro de la Tierra).
El problema admite solución de semejanza (Reduction by dimension similarity). Tomaremos el eje z hacia abajo.
| > | eqT:=T(eta)=A+B*erf(eta);eqT:=T(z)=T[0]+(T[infinity]-T[0])*erf(z/sqrt(4*a*t));eqTp:=diff(%,z);Tp0:=eval(subs(z=0,rhs(%)));eqq0:=q(0)=k*Tp0;t_Kelvin:=factor(solve(dTdz0=Tp0,t));t_Kelvin_:=evalf(subs(T[infinity]=Tinf,T[0]=Ts,a=aK,dat,t_Kelvin));'t_Kelvin_'=%/(86400*365*1e6*s_/Ma_); |
![diff(T(z), z) = `/`(`*`(`+`(T[infinity], `-`(T[0])), `*`(exp(`+`(`-`(`/`(`*`(`/`(1, 4), `*`(`^`(z, 2))), `*`(a, `*`(t)))))))), `*`(`^`(Pi, `/`(1, 2)), `*`(`^`(`*`(a, `*`(t)), `/`(1, 2)))))](images/p78_6.gif) |
![`/`(`*`(`+`(T[infinity], `-`(T[0]))), `*`(`^`(Pi, `/`(1, 2)), `*`(`^`(`*`(a, `*`(t)), `/`(1, 2)))))](images/p78_7.gif) |
![q(0) = `/`(`*`(k, `*`(`+`(T[infinity], `-`(T[0])))), `*`(`^`(Pi, `/`(1, 2)), `*`(`^`(`*`(a, `*`(t)), `/`(1, 2)))))](images/p78_8.gif) |
![`/`(`*`(`^`(`+`(T[0], `-`(T[infinity])), 2)), `*`(Pi, `*`(a, `*`(`^`(dTdz0, 2)))))](images/p78_9.gif) |
i.e., la Tierra tendría unos 50 millones de años, lo cual apenas es un 1 % del valor verdadero, 4500 millones de años, que se explica por la contribución de la desintegración radioactiva, descubierta por Becquerel años más tarde (1896).
b) Estimar si el modelo de Tierra plana es apropiado.
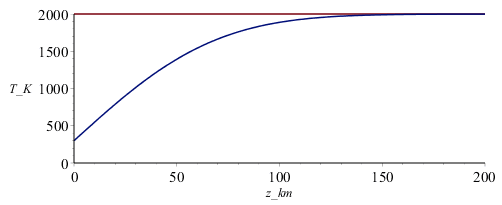
Habrá que ver cuánto habría penetrado el enfriamiento, para ver si es comparable con el radio de la Tierra. Para ello puede representarse el perfil de temperatura (o su pendiente) con este modelo.
| > | Tactual=T(x,t_Kelvin);Tactual_:=evalf(subs(t=t_Kelvin_,T[infinity]=Tinf,T[0]=Ts,a=aK,dat,rhs(eqT)));dTdz_actual_:=evalf(subs(t=t_Kelvin_,T[infinity]=Tinf,T[0]=Ts,a=aK,dat,rhs(eqTp)));plot(subs(z=z_km*1000,dat,SI0,[Tinf,Tactual_]),z_km=0..200,T_K=0..2000);plot(subs(z=z_km*1000,dat,SI0,dTdz_actual_),z_km=0..200,dT_dx_K_m=0..0.025); |
![Tactual = T(x, `/`(`*`(`^`(`+`(T[0], `-`(T[infinity])), 2)), `*`(Pi, `*`(a, `*`(`^`(dTdz0, 2))))))](images/p78_12.gif) |
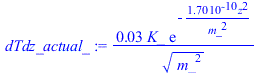 |
 |
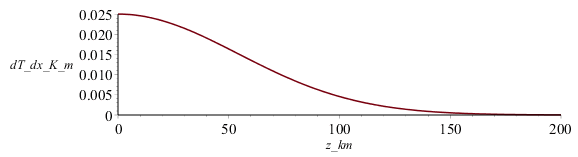 |
Vemos que el enfriamiento sólo es apreciable en los primeros 100 km (la inflexión en la pendiente tiene lugar a unos 50 km de profundidad), mucho menor que los 6370 km de radia de la Tierra, por lo que se concluye que la aproximación plana es válida.
c) Comparar el flujo de calor geotérmico con el de radiación al espacio exterior, como cuerpo negro.
| > | q_geo:=k*diff(T(z),z);q_out:=epsilon*sigma*(T(0)^4-Tcbr^4);Tcbr=2.7*K_;q_out_:=subs(dat,sigma*Ts^4);q_geo_:=subs(dat,k*dTdz0);datE:=Ts=288*K_,epsilon=0.6;q_out_real:=subs(datE,dat,epsilon*sigma*Ts^4); |
i.e., el flujo geotérmico, 0,035 W/m2, es despreciable frente al que emite la Tierra, 460 W/m2. Bueno, la Tierra está a una temperatura superficial media de 288 K y su emisividad media es del 60 %, por lo que solo emite 234 W/m2, que se compensa con la absorción solar (otros 234 W/m2, teniendo en cuenta que solo se absorbe el 70 % de los 1360 W/m2 del flujo solar normal).
d) Calcular el flujo de calor geotérmico correspondiente a un modelo del interior de la Tierra consistente en un núcleo de 3500 km de radio de hierro fundido a unos 5000 K (a muy alta presión), y un manto externo cuyas propiedades se asimilan a las de la sílice. Estimar un valor medio de generación interna de energía (desintegración nuclear) que ajuste al valor medido de 0,07 W/m2 del flujo medio en superficie.
Ahora se trata de un problema de conducción de calor estacionario, con fuentes, en geometría esférica.
| > | deq:=0=(1/r)^2*diff(r^2*diff(T(r),r),r)+phi/k;dsol:=dsolve([deq,T(RG)=TG,T(R)=Ts],T(r));dsol_phi0:=subs(R=R[T],RG=R[T]-zG,phi=0,dat,SI0,dsol);q0=-k*Diff(T(r),r)[r=RT];q0_phi0:=q0=subs(r=R[T],dat,-k*diff(subs(dsol_phi0,T(r)),r));%*1e3;dsol_phi:=expand(subs(R=R[T],RG=R[T]-zG,dat,SI0,dsol));q0_phi:=q0=subs(dat,q0);q0_phi:=subs(R=R[T],dat,SI0,q0=subs(r=R[T],RG=R[T]-zG,dat,SI0,-k*diff(subs(dsol,T(r)),r)));phi=subs(dat,solve(%,phi))*W_/m_^3; |
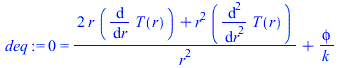 |
i.e., el flujo de calor geotérmico sería solo de 0,85 mW/m2 sin radioactividad, y para que llegase al valor dado de 0,07 W/m2 se necesitaría una liberación radioactiva media de unos unos 50 nW/m3 (48e-9 W/m3).
e) Calcular el flujo de calor geotérmico correspondiente a un modelo de corteza terrestre de 35 km de espesor, con unos 900 K en la parte inferior. Estimar un valor medio de generación interna de energía (desintegración nuclear) que ajuste al valor medido de 0,07 W/m2 del flujo medio en superficie.
| > | eqPlanar:=q0=k*(Tm-T0)/zm;q0_crust_:=subs(dat,rhs(%));eqPlanar_phi:=q0=k*(Tm-T0)/zm+phi*zm/2;phi[crust]=subs(dat,SI0,solve(%,phi))*1e6*mu*W_/m_^3; |
i.e., el flujo de calor geotérmico sería de 0,025 W/m2 sin radioactividad, y se necesitaría una liberación radioactiva media de unos 2,6 microvatios por metro cúbico (2,6e-6 W/m3) para que el flujo alcanzase el valor medido de 0,07 W/m2.
Según estos modelos, se deduce que la desintegración radioactiva es mayor en la corteza que en el manto. Tanto el gradiente geotérmico como la liberaciín radioactive dependen de la latitud y la longitud del lugar. Los elementos que más contribuyen a esta disipación son el uranio, el potasio, y el torio.
La discontinuidad a los casi 3000 km de profundidad que separa el manto del núcleo se llama discontinuidad de Gutenberg.
Ref. :Thomson, W., 1863, On the secular cooling of the Earth, Philos. Mag. Ser. 4:25, pp. 157-170.
| > |