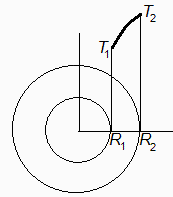
>	restart:#"m11_p77"

A través de un cuerpo cilíndrico de radio interior la mitad del exterior, hay un flujo de calor estacionario tal que la temperatura en la cara exterior es el doble que en la interior. A partir de un cierto instante las paredes pueden considerarse adiabáticas. Se pide:

a) Temperatura final.

b) ¿Y si el cuerpo fuese esférico?

c) ¿Y si hubiera sido la temperatura en la cara exterior la mitad de la interior?

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

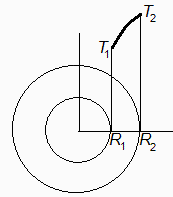
a) Temperatura final.

El 2º Principio enseña que al final la temperatura será uniforme, T0, y el 1er Principio enseña que la energía interna se conserva por ser adiabático y rígido.

Sea R1 el radia interior, R2 el exterior, y T1 y T2 las correspondientes temperaturas iniciales.

Ecuación del calor unidimensional estacionaria plana (n=0), cilíndrica (n=1), o esférica (n=2):

>	eqHT_1D:=0=(1/r^n)*diff(r^n*diff(T(r),r),r);eqHT_1D_cyl:=subs(n=1,%);sol_cyl1:=dsolve({%,T(R1)=T1,T(R2)=T2},T(r));

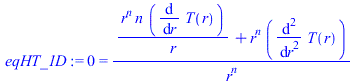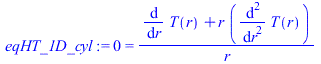	(1)

Para el primer caso:

>

eqR:=R2=2*R1;eqTcase1:=T2=2*T1;sol_cyl1_:=subs(eqR,eqTcase1,sol_cyl1);plot([[[1,0],[1,2]],[[2,0],[2,2]],subs(R1=1,T1=1,rhs(%))],r=1..2,T_T1=0..2,view=[0..2,0..2]);eqBE:=Int(2*Pi*r*T(r),r=R1..R2)=Pi*(R2^2-R1^2)*T0;eqBE_:=value(subs(sol_cyl1,eqR,eqTcase1,%));T0_cyl1:=evalf(solve(%,T0));T0_cyl1_:=subs(T1=(2/3)*Tmean,%);eqTmean:=Tmean=(T1+T2)/2;

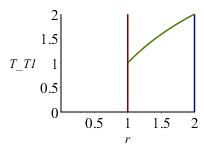	(2)

i.e. en el proceso de relajación con caras aisladas, la temperatura final (T0) es un 7% superior a la temperatura media (como era de esperar por la forma convexa del perfil T(r) en la figura).

b) ¿Y si el cuerpo fuese esférico?

>	eqHT_1D_sph:=subs(n=2,eqHT_1D);sol_sph1:=dsolve({%,T(R1)=T1,T(R2)=T2},T(r));

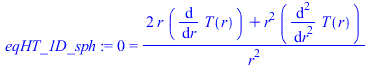	(3)

Para el primer caso:

>	sol_sph1_:=subs(eqR,eqTcase1,sol_sph1);plot([[[1,0],[1,2]],[[2,0],[2,2]],subs(R1=1,T1=1,rhs(%))],r=1..2,T_T1=0..2,view=[0..2,0..2]);eqBE:=Int(4*Pi*r^2*T(r),r=R1..R2)=(4/3)*Pi*(R2^3-R1^3)*T0;eqBE_:=value(subs(sol_sph1,eqR,eqTcase1,%));T0_sph1:=evalf(solve(%,T0));T0_sph1_:=subs(T1=(2/3)*Tmean,%);

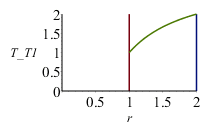	(4)

i.e. en el proceso de relajación con caras aisladas en el caso esférico, la temperatura final es un 14 % superior a la temperatura media (el perfil T(r) es ahora más convexo).

c) ¿Y si hubiera sido la temperatura en la cara interior la mitad de la exterior?

Para el caso cilíndrico:

>

eqR:=R2=2*R1;eqTcase2:=T2=T1/2;sol_cyl1_:=subs(eqR,eqTcase2,sol_cyl1);plot([[[1,0],[1,2]],[[2,0],[2,2]],subs(R1=1,T1=1,rhs(%))],r=1..2,T_T1=0..2,view=[0..2,0..2]);eqBE:=Int(2*Pi*r*T(r),r=R1..R2)=Pi*(R2^2-R1^2)*T0;eqBE_:=value(subs(sol_cyl1,eqR,eqTcase2,%));T0_cyl1:=evalf(solve(%,T0));T0_cyl1_:=subs(T1=(2/3)*Tmean,%);eqTmean:=Tmean=(T1+T2)/2;

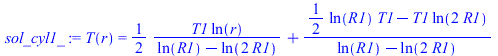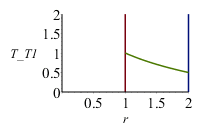	(5)

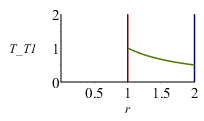
Para el caso esférico:

>	sol_sph1_:=subs(eqR,eqTcase2,sol_sph1);plot([[[1,0],[1,2]],[[2,0],[2,2]],subs(R1=1,T1=1,rhs(%))],r=1..2,T_T1=0..2,view=[0..2,0..2]);eqBE:=Int(4*Pi*r^2*T(r),r=R1..R2)=(4/3)*Pi*(R2^3-R1^3)*T0;eqBE_:=value(subs(sol_sph1,eqR,eqTcase2,%));T0_sph1:=evalf(solve(%,T0));T0_sph1_:=subs(T1=(2/3)*Tmean,%);

	(6)

Vemos que ahora las temperaturas de equilibrio son menores que la media (como corresponde a perfiles T(r) cóncavos).

En una pared plana es siempre T0=Tmean.

>