| > | restart:#"m11_p76" |
11.63. Para calentar una habitación de 4·6 m2 se va a disponer bajo el suelo una parrilla de 10 tubos de agua equiespaciados, de 12 mm de diámetro exterior y 6 m de longitud, cuyos ejes están 25 mm por debajo del nivel del suelo. Suponiendo que para mantener el aire de la habitación a 21 ºC se necesita añadir 3 kW para compensar las pérdidas al exterior, y tomando valores representativos de 1 W/(m·K) para la conductividad de los materiales del suelo y de 10 W/(m2·K) para la convección natural en el aire, se pide:
a) Temperatura media necesaria en el circuito del agua.
b) Temperatura del suelo.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots): |
| > | dat:=[A=4*6*m_^2,N=10, D=0.012*m_,L=6*m_,Ly=4*m_,z=0.025*m_,T0=(21+273.15)*K_,Q=3000*W_,k=1*W_/(m_*K_),h=10*W_/(m_^2*K_)]; |
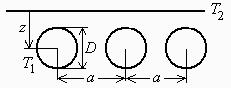
Se va a resolver con ayuda del factor geométrico de forma conductivo, S, tomado de la Tabla 1.
| > | dat:=op(dat),Const,SI2,SI1:eqS:=S=2*Pi*L*N/ln((2*a/(Pi*D))*sinh(2*Pi*z/a)); |
 |
(1) |
a) Temperatura media necesaria en el circuito del agua.
b) Temperatura del suelo.
Basta plantear los flujos de calor en serie:
| > | eq1:=Q=k*S*(T2-T1);eq2:=Q=h*A*(T1-T0);eqa:=a=Ly/N;sol_:=op(subs(dat,solve(subs(eqS,eqa,dat,[eq1,eq2]),[T1,T2])));T1_:=TKC(subs(sol_,T1));T2_:=TKC(subs(sol_,T2)); |
| (2) |
i.e. el agua ha de estar a una temperatura media de 51 ºC, y el suelo quedaría a 33,5 ºC.
| > |