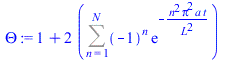
>	restart:#"m11_p75"

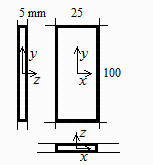
Se quiere comparar el comportamiento térmico de una pared de aluminio anodizado de 5 mm de espesor, con otra de igual espesor de CFRP. Ambas se van a suponer expuestas al vacío espacial por una cara, y aisladas con una manta térmica multicapa por la otra. Supóngase que en un estado inicial toda la pared está a 300 K. Se pide:

a) Temperaturas en estado estacionario cuando la pared recibe una radiación solar de 1370 W/m2.

b) Evolución de las temperaturas durante el transitorio.

c) Para la pared de CFRP se piensa realizar el ensayo siguiente. Partiendo del mismo estado inicial (300 K), se va a irradiar una franja de 2,5×10 cm2 de pared durante 5 segundos con una lámpara que da 2 W/cm2, Determinar el estado térmico que se alcanzaría si no hubiese pérdidas.

d) Evolución de las temperaturas durante el transitorio anterior (sin pérdidas).

e) Evaluar las pérdidas por conducción y radiación, para ver cuáles son mayores.

f) Resolver el problema unidimensional de la conducción en el CFRP a lo largo de la dirección x (i.e. perpendicular al lado mayor de la muestra), promediando las temperaturas en el espesor de 5 mm, correspondiente al calentamiento con la lámpara y teniendo en cuenta las pérdidas conductivas.

g) Comparar la evolución temporal de la temperatura en el centro de la parte de atrás de la muestra, con y sin pérdidas por conducción, con el resultado teórico para una irradiación instantánea sin pérdidas:

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):

>	su1:="Aluminio":su2:="CFRP":dat:=[L=0.005*m_,T0=300*K_,E0=1370*W_/m_^2,Lx=0.025*m_,Ly=0.1*m_,DtI=5*s_,E1=2e4*W_/m_^2,Tinf=2.7*K_];w:=Pi^2*a*t/L^2;Theta:=1+2*Sum((-1)^n*exp(-n^2*w),n=1..N);

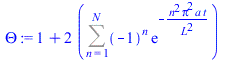>	dat:=op(dat),Const,SI2,SI1:datA:=rho=2800*kg_/m_^3,c=960*J_/(kg_*K_),k=120*W_/(m_*K_),alpha=0.2,epsilon=0.6;datC:=rho=1500*kg_/m_^3,c=1200*J_/(kg_*K_),k=1.5*W_/(m_*K_),alpha=0.9,epsilon=0.9,kpar=25*W_/(m_*K_);

	(1)

a) Temperaturas en estado estacionario cuando la pared recibe una radiación solar de 1370 W/m2.

>	eqBEstd:=alpha*E0=epsilon*sigma*(Tstd^4-Tinf^4);Tstd_A:=subs(datA,dat,SI0,solve(eqBEstd,Tstd)[1])*K_;Tstd_C:=subs(datC,dat,SI0,solve(eqBEstd,Tstd)[1])*K_;

	(2)

i.e. la pared de Al quedaría prácticamente a la misma temperatura (300 K) y ya no la estudiamos más, pero la de CFRP alcanzaría 394 K, por lo que tal vez convendría pintarla de blanco.

b) Evolución de las temperaturas durante el transitorio.

Para el caso del aluminio apenas hay transitoio porque Tstd=T0.

Para el CFRP, que pasa de T0=300 K a Tstd=394 K, puede suponerse que la temperatura solo depende del tiempo (i.e. que el perfil T(x) es casi plano en cada instante), ya que el tiempo de calentamiento ttot que se obtiene de m*c*DT=Qdot*ttot, ttot=1400 s (aproximando la entrada media por la mitad de la inicial), es mucho mayor que el tiempo de relajación conductiva, Dt=L^2/a=rho*c*L^2/k=30 s.

>	eqBEtot:=rho*L*c*dT/dt=alpha*E0-epsilon*sigma*(T^4-Tinf^4);ttot:=2*rho*L*c*('Tstd_C'-T0)/(alpha*E0);ttot_:=subs(datC,dat,%);eqDt_cond:=Dt=rho*c*L^2/k;eqDt_cond_:=subs(datC,dat,%);

	(3)

La EDO es integrable por separación de variables:

>

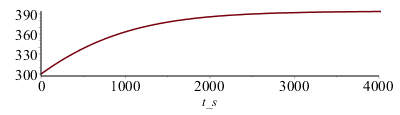
eqBEtot_:=Int(rho*L*c/rhs(eqBEtot),T)=Int(1,t);eqBEtot__:=subs(datC,dat,SI0,%);eqBEtot___:=evalf(value(lhs(%))-subs(T=300,value(lhs(%)))=value(rhs(%)));plot([lhs(eqBEtot___),T,T=300..400],t_s=0..4000);Inte:=(rho*L*c*T_/(4*alpha*E0))*(ln((T_+T)/(T_-T))+2*arctan(T/T_));eqBEtot_Tinf0:=subs(T_=T1,Inte)-subs(T_=T1,T=T0,Inte)=t;eqBEtot_Tinf0_:=evalf(subs(T1=Tstd_C,datC,dat,SI0,%));

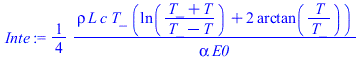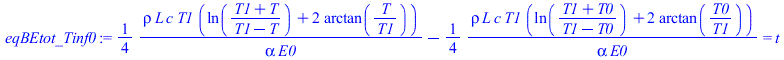	(4)

donde la última expresión algebraica se ha obtenido para Tinf=0.

Pero la ecuación diferencial suele resolverse numéricamente:

>	deq:=subs(datC,dat,SI0,rho*L*c*diff(T(t),t)=alpha*E0-epsilon*sigma*(T(t)^4-Tinf^4));sol_:=dsolve({deq,T(0)=subs(dat,SI0,T0)},T(t),numeric,range=0..4000);odeplot(sol_);

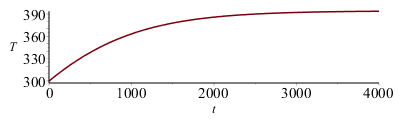Si se hubiera resuelto directamente el problema espacio-temporal, T(x,t), numéricamente, claro, el resultado sería similar. Veámoslo:

Sea N el nº de capas y M el nº de intervalos de tiempo usados en la discretización.

El intervalo espacial es Dx=L/N.

El intervalo temporal Dt lo elegiremos para que Fo<1/2; e.g. Fo=0.49 para que sea más rápido.

El tiempo total que durará el proceso será del orden de ttot=L^2/a=30 s, por lo que habrá que dar M=ttot/Dt saltos en el tiempo.

La discretización es:

>

eq11_24;eq_i:=subs(phi=0,h[lat]=0,epsilon[lat]=0,eq11_24_gen_);eq_0:=subs(phi=0,h[lat]=0,epsilon[lat]=0,h0=0,epsilon0=0,E0=0,eq11_24_0_);eq_N:=subs(TN=Tinf,phi=0,h[lat]=0,epsilon[lat]=0,hN=0,epsilonN=epsilon,EN=alpha*E0,eq11_24_N_);eqFo:=Fo=a*Dt/Dx^2;eqa:=eq11_5;eqDx:=Dx=L/N;eqDt:=Dt=solve(subs(eqa,eqDx,eqFo),Dt);eqM:=M=L^2/(a*Dt);

	(5)

Aluminio. Apenas hay transitorio pues la T casi no varía, y además sería muy rápido porque el tiempo de relajación  por conducción en 5 mm de Al es del orden de L^2/a=0.5 s.

CFRP. El transitorio será con perfil T(x) casi plano porque el tiempo de relajación por conducción en 5 mm de CFRP es del orden de L^2/a=25/0.83=30 s, y el tiempo de calentamiento es de unos 1400 s, como se ha visto antes.

>	N:=5;Fo_:=0.49;eqDx_:=subs(dat,eqDx);eqDt_:=subs(Fo=Fo_,datC,dat,eqDt);eqM_:=subs(eqDt_,datC,dat,eqM);eqM_:=M=5000;eqFo_:=subs(eqa,datC,eqDt_,eqDx_,dat,eqFo);datnum0:=op(subs(SI0,['N'=N,eqM_,eqDx_,eqDt_,eqFo_,datC,dat])):k=subs(datnum0,k);eqa_:=subs(datC,dat,eqa);

	(6)

Inicialización: T[i , j=0]=T0.

>	j:=0:for i from 0 to N do T[i,j]:=subs(datnum0,T0):od:i:='i':

Iteraciones.

>	M:=rhs(eqM_):for j from 0 to M-1 do eq_0_:=subs(datnum0,eq_0);assign(%);for i from 1 to N-1 do eq_i_:=subs(datnum0,eq_i);assign(%);od; i:='i':eq_N_:=subs(datnum0,eq_N);assign(%);od:i:='i':

Resultado.

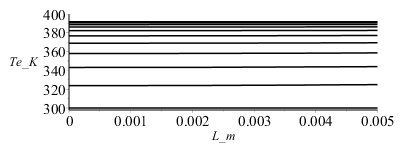
>	Mdis:=10:pl:=subs(datnum0,[seq([seq([L*(i/N),T[i,jdis*trunc(M/Mdis)]],i=0..N)],jdis=0..Mdis)]):plot(pl,L_m=0..0.005,Te_K=300..400,color=black);plot(subs(datnum0,[seq([seq([subs(datnum0,M*Dt)*(j/Mdis),T[i,j*trunc(M/Mdis)]],j=0..Mdis)],i=1..N)]),t_s=0..3000,T_K=300..400,color=black);

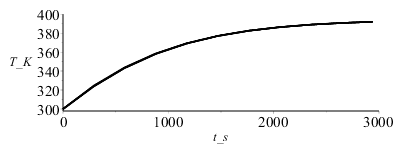vemos que la simplificación T(x,t)=T(t) era suficiente.

c) Para la medida de la conductividad térmica del CFRP se piensa realizar el ensayo siguiente. Partiendo del mismo estado inicial (300 K), se irradia una franja de 2,5×10 cm2 de pared durante 5 segundos con una lámpara que da 2 W/cm2, Determinar el estado térmico que se alcanzaría si no hubiese pérdidas.

Al final quedará a Tcte tal que m*c*DT=Int(alpha*E,t)

>	eqBE:=rho*L*c*(Tfin-T0)=Int(alpha*E,t=0..DtI);E=subs(dat,E1);Q:=Int(alpha*E,t=0..DtI)=subs(datC,dat,SI0,int(alpha*E1,t=0..DtI))*1e-3*kJ_/m_^2;Tfin_:=subs(datC,dat,T0+int(alpha*E1,t=0..DtI)/(rho*L*c));

	(7)

i.e. si no hubiera pérdidas, la pared quedaría a 310 K tras recibir los 90 kJ/m2.

d) Evolución de las temperaturas durante el transitorio.

Repetimos el cálculo de T(x,t), pero cambiando la E=cte por una E(t). Habrá que afinar el intervalo temporal (e.g. de Dt=0.58 s a DT=0.1 s o menor). La nueva discretización será:

>	i:='i':j:='j':N:='N':M:='M':T:='T':eq_i:=subs(phi=0,h[lat]=0,epsilon[lat]=0,eq11_24_gen_);eq_0:=subs(phi=0,h[lat]=0,epsilon[lat]=0,h0=0,epsilon0=0,E0=0,eq11_24_0_);eq_N:=subs(TN=Tinf,phi=0,h[lat]=0,epsilon[lat]=0,hN=0,epsilonN=0,EN=alpha*E1,eq11_24_N_);eqFo:=Fo=a*Dt/Dx^2;eqa:=eq11_5;eqDx:=Dx=L/N;

	(8)

>

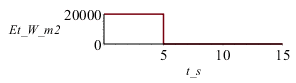
N:=25;eqDx_:=subs(dat,SI0,eqDx);Dt_:=0.02*s_:eqDt_:=Dt=subs(SI0,Dt_);eqM_:=M=750;k=subs(datC,k);eqFo_:=subs(eqa,datC,eqDt_,eqDx_,dat,SI0,eqFo);datnum0:=op(subs(SI0,['N'=N,eqM_,eqDx_,eqDt_,eqFo_,datC,dat])):k=subs(datnum0,k);Et:=piecewise(j<subs(dat,SI0,datnum0,DtI/Dt_),subs(dat,SI0,E1),0);plot(subs(j=t_s*s_/Dt_,Et),t_s=0..15,Et_W_m2=0..2e4);j:=0:To[0]:=subs(datnum0,T0):for i from 0 to N do T[i,j]:=subs(datnum0,T0):od:M:=rhs(eqM_):for j from 0 to M-1 do eq_0_:=subs(datnum0,eq_0);assign(%);To[j+1]:=rhs(eq_0_);for i from 1 to N-1 do eq_i_:=subs(datnum0,eq_i);assign(%);od; eq_N_:=subs(E1=Et,datnum0,eq_N);assign(%);od:pl1:=[seq([j*Dt_/s_,To[j]],j=0..M-1)]:

>

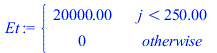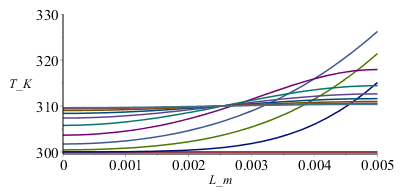
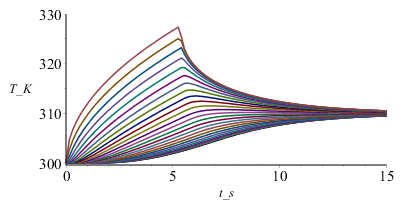
Mdis:=10:pl:=subs(datnum0,[seq([seq([L*(i/N),T[i,jdis*trunc(M/Mdis)]],i=0..N)],jdis=0..Mdis)]):plot(pl,L_m=0..0.005,T_K=300..330);Mdis:=100:plot(subs(datnum0,[seq([seq([subs(datnum0,M*Dt)*(j/Mdis),T[i,j*trunc(M/Mdis)]],j=0..Mdis)],i=0..N)]),t_s=0..15,T_K=300..330);Tlast:=To[M-1],seq(T[i,M-1],i=1..N);

	(9)

e) Evaluar las pérdidas por conducción y radiación, para ver cuáles son mayores.

Si partimos de que la pieza está a Tfin=310 K, en presencia de la radiación de fondo a Tinf=2.7 K, y lateralmente rodeada por el resto de la pared a T0=300 K, las pérdidas por conducción tras el calentamiento (5 s) pueden aproximarse por Qdot_cond=k*A*DT/L, pero usando la k del CFRP paralelo a la fibra, con A=área lateral de contacto, DT=Tfin-T0, y L una longitud carácterística que tomaremos como Lx, aunque esto solo valdría para calentamiento rápido de la zona iluminada, si no, el gradiente sería menor. Sólo contabilizaremos el perímetro de los lados largos, i.e. A=2*Ly*Lz.

>	Qdot_cond:=kpar*(2*L*Ly)*(Tfin-T0)/Lx;Qdot_cond_:=subs(Tfin=Tfin_,datC,dat,%);Qdot_rad:=epsilon*Lx*Ly*sigma*(Tfin^4-Tinf^4);Qdot_rad_:=subs(Tfin=Tfin_,datC,dat,%);

	(10)

i.e. pierde unos 10 W por conducción al resto de la pared de CFRP, y unos 1,2 W por radiación al vacío (no se tiene en cuenta la radiación solar porque se piden las "pérdidas radiativas", no las ganancias; la radiación solar aportaría alpha*E*Lx*Ly=3,1 W).

f) Resolver el problema unidimensional de la conducción en el CFRP a lo largo de la dirección x (i.e. perpendicular al lado mayor de la muestra), promediando las temperaturas en el espesor de 5 mm, correspondiente al calentamiento con la lámpara y teniendo en cuenta las pérdidas conductivas.

El ancho de interés de la muestra es Lx=25 mm, y tenemos que coger un trozo mucho mayor de pared exterior. Como el problema es simétrico, tomaremos el origen en el eje de simetría, siendo los primeros L1=12,5 mm los expuestos a la lámpara, y acabando la simulación de la pared en L2=50 mm >> L1. El aporte de energía de la lámpara es equivalente a una generación interna volumétrica phi de valor qdot/L=1e4/5e-3=2e6 W/m^3, limitado en el espacio al tramo x<L1=12,5 mm y limitada en el tiempo a t<DtI=5 s.

>

L1:=0.0125;L2:=0.05;N:=25;M:=500;eqDx:=Dx=L2/N;Dt_:=0.1;eqFo_:=subs(Dt=Dt_,eqDx,eqa,k=kpar,datC,dat,SI0,eqFo);i:='i':j:='j':eq_i:=subs(phi=phi[i,j],p=0,eq11_24_gen_);Nphi:=trunc(subs(eqDx,L1/Dx))-1;Mphi:=trunc(subs(dat,SI0,DtI/Dt_));for j from 0 to M-1 do for i from 0 to N do phi[i,j]:=0; if (i<Nphi and j<Mphi) then phi[i,j]:=subs(dat,SI0,E1/L); end if;od;od;i:='i':j:='j':eq_0:=subs(phi=phi[0,j]/2,h[lat]=0,epsilon[lat]=0,h0=0,epsilon0=0,E0=0,eq11_24_0_);eq_N:=subs(TN=T0,phi=0,h[lat]=0,epsilon[lat]=0,hN=0,epsilonN=0,EN=0,eq11_24_N_);datnum0:=op(subs(SI0,['N'=N,'M'=M,eqDx,'Dt'=Dt_,eqFo_,k=kpar,datC,dat])):k=subs(datnum0,k);

	(11)

Inicialización: T[i , j=0]=T0.

>	T:='T':j:=0:for i from 0 to N do T[i,j]:=subs(datnum0,T0):od:To[0]:=subs(datnum0,T0):

Iteraciones.

>	for j from 0 to M-1 do eq_0_:=subs(datnum0,eq_0);assign(%);To[j+1]:=rhs(eq_0_);for i from 1 to N-1 do eq_i_:=subs(datnum0,eq_i);assign(%);od; eq_N_:=subs(datnum0,eq_N);assign(%);od:

Solución (se han separado los perfiles durante el calentamiento, t<5 s, y durante el enfriamiento, t>5 s).

>

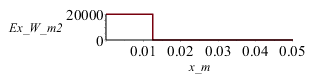
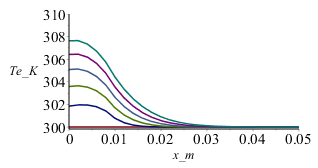
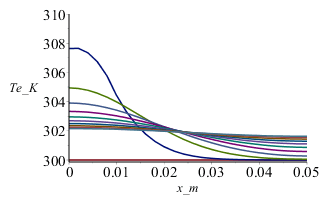
plot(piecewise(x_m<subs(dat,SI0,Lx/2),subs(dat,SI0,E1),0),x_m=0..0.05,Ex_W_m2=0..2e4);Mdis:=50:pl:=subs(datnum0,[seq([seq([L2*(i/N),T[i,jdis*trunc(M/Mdis)]],i=0..N)],jdis=0..Mdis/10)]):plot(pl,x_m=0..0.05,Te_K=300..310);Mdis:=10:pl:=subs(datnum0,[seq([seq([L2*(i/N),T[i,jdis*trunc(M/Mdis)]],i=0..N)],jdis=0..Mdis)]):plot(pl,x_m=0..0.05,Te_K=300..310);Mdis:=50:plot(subs(datnum0,[seq([seq([subs(datnum0,M*Dt)*(j/Mdis),T[i,j*trunc(M/Mdis)]],j=0..Mdis)],i=1..N)]),t_s=0..50,T_K=300..310);pl2:=[seq([j*Dt_,To[j]],j=0..M-1)]:

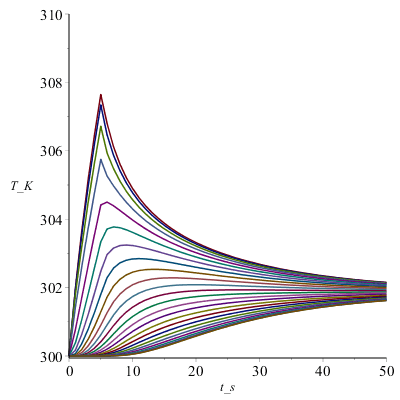Como puede apreciarse, al principio la lámpara calienta rápidamente la muestra (de 0,0125 m a cada lado del origen de x=0), y luego se va disipando el calor por conducción al resto de la pared, acabando todo a 300 K si la paraed es muy grande (en esta simulación, como se ha supuesto que la pared solo llegaba a L=50 mm, i.e. 4 veces la anchura iluminada Lx=12,5 mm, la temperatura tras la irradiación no decae a 300 K sino a 302,5 K (i.e. los 10 K de sobrecalentamiento de los 12,5 mm irradiados se reparte en un volumen 4 veces mayor).

g) Comparar la evolución temporal de la temperatura en el centro de la parte de atrás de la muestra, con y sin pérdidas por conducción, con el resultado teórico para una irradiación instantánea sin pérdidas:

Antes conviene estudiar un poco la función Theta dada.

>	N:='N':Theta:=1+2*Sum((-1)^n*exp(-n^2*t/tau),n=1..N);tau:=t/w;Tback:=T0+(Tfin-T0)*(1+2*Sum((-1)^n*exp(-n^2*w),n=1..N));plot([seq(subs(t=t_tc,a=1,L=1,value(Theta)),N=1..4)],t_tc=0..0.5,theta=-0.1..1);

Fig. 1. Representación de la función dada, Theta(t) (para valores unitarios de los demás parámetros), tomando N=1, 2, 3, y 4 términos del desarrollo.

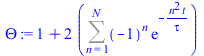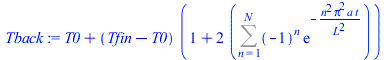Vemos que Theta no está definida para t=0 (va dando -1 o +1 según la N), pero enseguida se estabiliza. Tomamos N=5 términos.

El proceso de penetración del calor a través de los 5 mm de pared, T(z,t), sin pérdidas laterales, ya se ha calculado antes en el apartado d), y la comparación con la solución teórica:

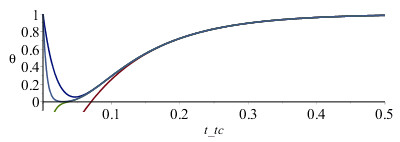
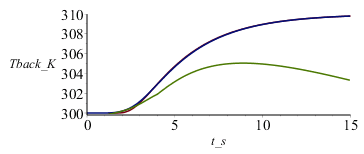
>	Tback_:=expand(subs(N=7,Tfin=Tfin_,eqa,datC,dat,SI0,evalf(value(Tback))));plot([subs(t=t_s,Tback_),pl1],t_s=0..15,Tback_K=300..310);

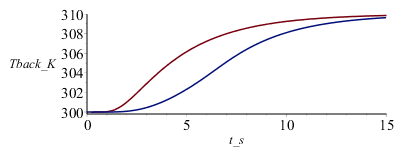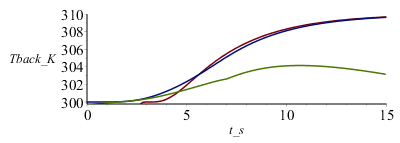
no concuerda bien; parece que existe una diferencia en el origen de tiempos, lo cual es atribuible a que el modelo teórico es válido para deposición instantánea de energía, mientras que en la simulación la deposición duraba DtI=5 s. Si ajustamos el origen de tiempos teórico al punto medio del periodo de irradiación, la concordancia es mucho mejor:

>	Dt_adj:=DtI/2;plot([subs(t=t_s-Dt_adj,dat,SI0,Tback_),pl1],t_s=0..15,Tback_K=300..310);

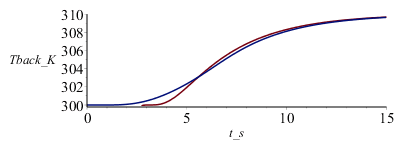aunque las pendientes todavía difieren apreciablemente:

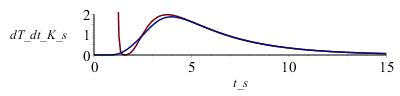
>	pl1dif:=[seq([op(1,op(i,pl1)),(op(2,op(i+1,pl1))-op(2,op(i,pl1)))/(op(1,op(i+1,pl1))-op(1,op(i,pl1)))],i=1..749)]:plot([subs(t=t_s-Dt_adj,dat,SI0,diff(Tback_,t)),pl1dif],t_s=0..15,dT_dt_K_s=0..2);

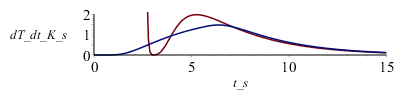que solo hay que considerar a partir de unos t=4 s porque para t<4 s habría que tomar muchos más términos en el desarollo teórico.

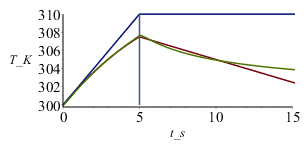
Para determinar la solución con pérdidas habría que resolver el problema bidimensional, T(x,z,t) (y si no se desprecian las pérdidas en la otra dirección, el problema tridimensional, T(y,x,z,t)), pero una aproximación sencilla sería modelizar las pérdidas laterales conductivas calculadas en el apartado f). Si usamos un modelo lineal con pérdidas proporcionales al tiempo transcurrido, DTloss=c*t, con un coeficiente empírico c=0,5 para ajustar las pérdidas al final del periodo de irradiación, tenemos:

>

Ttsin:=subs(dat,SI0,piecewise(t<DtI,T0+(Tfin_-T0)*t/DtI,Tfin_));pl3:=[seq([(i-1)/10,subs(t=(i-1)/10,Ttsin)],i=1..500)]:Ttcon:=subs(dat,SI0,piecewise(t<DtI,T0+(Tfin_-T0-0.5*t)*t/DtI,Tfin_-0.5*t));pl4:=[seq([(i-1)/10,subs(t=(i-1)/10,Ttcon)],i=1..500)]:plot([pl4,pl3,pl2,subs(dat,SI0,[[DtI,T0],[DtI,Tfin_]]),9999],t_s=0..15,T_K=300..310);pl5:=[seq([op(1,op(i,pl1)),op(2,op(i,pl1))-subs(t=op(1,op(i,pl1))-2,Ttsin-Ttcon)],i=1..749)]:plot([subs(t=t_s-Dt_adj,dat,SI0,Tback_),pl1,pl5],t_s=0..15,Tback_K=300..310);

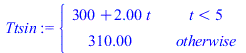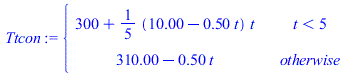Conclusión: las pérdidas por conducción lateral en la banda iluminada (de 25x5 mm2) son demasiado grandes para que el modelo teórico se ajuste al comportamiento real, e incluso si se aislara laterlmente la banda, el ajuste no es perfecto por la duración finita de la irradiación (aunque puede verse que si esta durase menos, el ajuste sería perfecto, como puede comprobarse cambiando los valores de DtI=5 s y E1=2e4*W_/m_^2, por los nuevos DtI=2 s y E1=5e4*W_/m_^2 para mantener la misma deposición global.

>

>

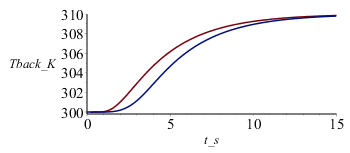NOTA. El modelo teórico se usa a veces para determinar la difusividad térmica del material por ajuste del valor máximo de la pendiente dT/dt en la cara trasera, tal que a=0,17*(L^2/DT)*dT/dt. Puede comprobarse con nuestra simulación numérica sin pérdida:

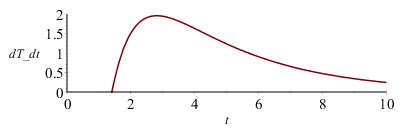
>	dT_dt:=diff((subs(N=2,value(Tback))),t);plot(subs(Tfin=Tfin_,eqa,datC,dat,SI0,%),t=0..10,'dT_dt'=0..2);d2T_dt2:=diff(dT_dt,t);t_:=solve(d2T_dt2=0,t);dT_dt_max:=subs(t=t_,dT_dt);dT_dt_max_=evalf(%);a_:=solve(%,a);

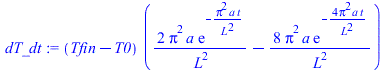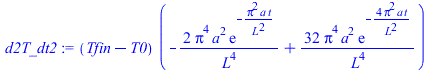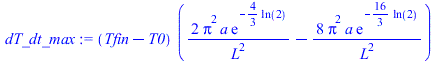	(12)

Por ejemplo, para nuestra pared de CFRP, DT=10 K y dT/dt max =2 K/s (ver Fig.dT_dt), así que a=0,17*5^2*2/10=0,85e-6 m^2/s, que coincide con el del CFRP dado por eqa.

>