>	restart:#"m11_p72"

Considerar el muro sur de una casa, que tiene 0,25 m de espesor, 0,7 W/(mK) de conductividad, 0,9 de emisividad, y 0,6 de absortancia sola, el cual está expuesto a una radiación solar de 700 W/m2. El interior de la casa está a 22 ºC, y el exterior a 5 ºC. Los coeficientes de transferencia de calor por convección sobre las superficies interior y exterior del muro son 6 W/(m2K) y 25 W/(m2K) respectivamente. Suponiendo régimen estacionario, se pide:
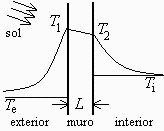
a) Esquematizar el problema, representando los flujos de calor y el perfil de temperatura esperado.
b) Plantear el balance de flujo de calor en las caras interior y exterior de la pared.
c) Calcular las temperaturas de las caras interior y exterior de la pared, suponiendo emisividad nula.
d) Calcular las temperaturas de las caras interior y exterior de la pared con la emisividad dada.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	dat:=[L=0.25*m_,E=700*W_/m_^2,alpha=0.6,Ti=(22+273.15)*K_,Te=(10+273.15)*K_,hi=6*W_/(m_^2*K_),he=25*W_/(m_^2*K_),k=0.7*W_/(m_*K_),epsilon=0.9];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Esquematizar el problema, representando los flujos de calor y el perfil de temperatura esperado.

Ver figura anterior. NOTA: hasta no hacer los cálculos, no se puede saber si el flujo de calor en la pared es hacia adentro (por la insolación) o hacia afuera (por la calefacción interior).

b) Plantear el balance de flujo de calor en las caras interior y exterior de la pared.

>	eqBE1:=E*alpha=epsilon*sigma*(T1^4-T0^4)+he*(T1-Te)+k*(T1-T2)/L;eqBE2:=k*(T1-T2)/L=epsilon*sigma*(T2^4-Ti^4)+hi*(T2-Ti);

c) Calcular las temperaturas de las caras interior y exterior de la pared, suponiendo emisividad nula.

>	sol0_:=subs(dat,solve(subs(epsilon=0,{eqBE1,eqBE2}),{T1,T2}));

i.e., si no emitiera, la cara exterior quedaría a 27 ºC y la interior a 24 ºC.

d) Calcular las temperaturas de las caras interior y exterior de la pared con la emisividad dada.

>	sol1_:=fsolve(subs(dat,SI0,{eqBE1,eqBE2}),{T1,T2});T1_:=subs(sol1_,T1)*K_;T1=TKC(%);T2_:=subs(sol1_,T2)*K_;T2=TKC(%);

i.e., la cara exterior queda a 25 ºC y la interior a 23 ºC.

>