>	restart:#"m11_p71"

Considérese una luneta térmica trasera de un vehículo, en la cual hay una serie de resistencias eléctricas horizontales equiespaciadas 4 cm, pegadas por el interior de una lámina de vidrio de 5 mm de espesor. Por cada conductor eléctrico se disipan 20 W/m y, aunque el hilo es muy delgado y el perfil de temperaturas en el vidrio no es homogéneo ni vertical ni transversalmente (se admite que es homogéneo a lo largo de los cables), se va a considerar en este problema que la temperatura en el vidrio sólo varía en su espesor. Se pide:
a) Perfil de temperatura en el vidrio, en un estado estacionario, con 18 ºC de temperatura del aire interior (tómese un coeficiente convectivo de 5 W/m2•K)), 8 ºC de temperatura del aire exterior (tómese un coeficiente convectivo de 50 W/m2•K)), y la resistencia apagada.
b) Plantear el problema estacionario con la resistencia encendida, enumerando ecuaciones e incógnitas.
c) Resolver el problema anterior, determinando las temperaturas en las caras del vidrio.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Vidrio_crown":dat:=[d=0.04*m_,L=0.005*m_,qL=20*W_/m_,Ti=(18+273.15)*K_,hi=5*W_/(m_^2*K_),Te=(-8+273.15)*K_,he=50*W_/(m_^2*K_)];

Eqs. const.:

>	Sdat:=get_sol_data(su):dat:=op(dat),Sdat,Const,SI2,SI1:k=subs(dat,k);

a) Perfil de temperatura en el vidrio, en un estado estacionario, con 18 ºC de temperatura del aire interior (tómese un coeficiente convectivo de 5 W/m2•K)), 8 ºC de temperatura del aire exterior (tómese un coeficiente convectivo de 50 W/m2•K)), y la resistencia apagada.

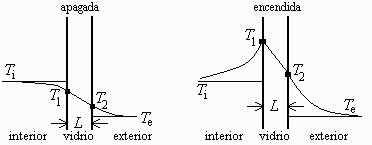
Se trata de la transmisión de calor desde dentro hacia afuera por convección-conducción-convección), Figura 1a.

Sea q el flujo de calor unitario (W/m2).

>	eq1:=q=hi*(Ti-T1);eq2:=q=k*(T1-T2)/L;eq3:=q=he*(T2-Te);sol_:=subs(dat,solve({eq1,eq2,eq3},{q,T1,T2}));

i.e. saldrían 115 W/m2, y las caras del vidrio estarían a -5 ºC y -6 ºC (con estas temperaturas, si el aire llega a saturarse de vapor, se formaría escarcha).

b) Plantear el problema estacionario con la resistencia encendida, enumerando ecuaciones e incógnitas.

Puede hacerse como antes pero con dos flujos distintos que han de sumar lo que aportan las resistencias, o planteando los balances energéticos en las interfases:

>	eqBE1:=qA=hi*(T1-Ti)+k*(T1-T2)/L;eqBE2:=k*(T1-T2)/L=he*(T2-Te);

Se trata de dos ecuaciones con dos incógnitas, T1 y T2, pues el flujo por unidad de área que aportan las resistencias será

>	qA:=qL/d;qA_:=subs(dat,%);

c) Resolver el problema anterior, determinando las temperaturas en las caras del vidrio.

>	sol1_:=subs(dat,solve({eqBE1,eqBE2},{T1,T2}));

i.e. la cara interior queda a 6 ºC y la exterior a 3 ºC. Con estas temperaturas, y conocidas las condiciones higrométricas ambientes, se vería si se produce condensación del vapor o no.

Nótese que la suposición inicial en la Fig. 1b no es adecuada, pues la disipación térmica es tan pequeña que no llega a calentar ni siquiera esa cara por encima de la temperatura del aire próximo. También estaba muy exagerada la caída de temperatura en el vidrio, por conducción, que es mucho menor que los saltos convectivos.

>