>	restart:#"m11_p68"

Un perfil de acero con forma de triángulo rectángulo cuyos catetos miden 2 y 3 cm, tiene 90 cm de longitud, y una resistencia eléctrica de 24  y tamaño despreciable embebida a un tercio de su longitud. Se quiere estudiar la transmisión de calor al ambiente, que está a 20 ºC y cuyo coeficiente convectivo se supone que es de 10 W/(m2•K), cuando se hace pasar una corriente eléctrica de 1 A por la resistencia (aislada eléctricamente). En particular, para el régimen estacionario, se pide:
a) Plantear el problema en forma diferencial (con las condiciones de contorno).
c) Calcular las temperaturas extremas y los flujos de calor hacia cada lado.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Acero":dat:=[Lt=0.9*m_,A=(0.02*0.03/2)*m_^2,p=(0.02+0.03+sqrt(0.02^2+0.03^2))*m_,Omega=24*ohm_,Tinf=(20+273.15)*K_,h=10*W_/(m_^2*K_),I=1*A_,Qt=24*W_,f=1/3];

Eqs. const.:

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a) Plantear el problema en forma diferencial (con las condiciones de contorno).

Se resuelve cada tramo de varilla por separado (para evitar la singularidad).

Tomamos los ejes siempre con el centro en la resistencia (x=0), y hacia afuera hasta x=L (que será L=Lt(2/3) en un caso y L=Lt(1/3) en el otro (ver figura).

Tomando un elemento genérico de longitud diferencial de varilla (desde x hasta x+dx), el balance energético es:

>	eq1:=subs(dA=0,epsilon=0,phi=0,eq11_12);eq1:=eq11_14;eqCC0:=Q0=-k*A*diff(T(x),x)[0];eqCCL:=diff(T(x),x)[L]=0;eqm:=eq11_13;eqm_:=evalf(subs(dat,eqm));

Nótese que la formulación es la misma para ambos trozos, y sólo cambian los valores de Q0 y L.

La solución del problema es fácil, pero no es necesario hacerla porque viene en los libros de texto (solución estacionaria con un flujo dado en un extremo y el otro libre). También se podría hacer a partir de la solución para una varilla con temperatura fija en un extremo y libre en el otro.

>	sol:=dsolve({subs(T[infinity]=Tinf,eq1),D(T)(0)=-Q0/(k*A),D(T)(L)=0},T(x));expand(convert(%,trig));eq:=T(x)=Tinf+(Q0/sqrt(p*h*k*A))*cosh(m*(L-x))/sinh(m*L);

b) Calcular las temperaturas extremas.

Con la solución genérica anterior aplicada a cada tramo, se obliga a que las temperaturas en x=0 sean iguales (T0) y a que la suma de los flujos hacia cada lado sumen los 24 W totrales.

>

eq10:=T0=T1(x)[x=0];eq10_:=T0=evalf(subs(x=0,Q0=Q01,L=Lt*(1-f),eqm_,dat,SI0,rhs(eq)));eq20:=T0=T2(x)[x=0];eq20_:=T0=evalf(subs(x=0,Q0=Q02,L=Lt*f,eqm_,dat,SI0,rhs(eq)));eq12:=Q01+Q02=Qt;eqs:={eq10_,eq20_,subs(dat,SI0,eq12)};sol:=solve(eqs,{T0,Q01,Q02});T1_:=evalf(subs(Q0=Q01,L=Lt*(1-f),eqm_,sol,dat,SI0,rhs(eq)));T2_:=evalf(subs(Q0=Q02,L=Lt*f,eqm_,sol,dat,SI0,x=-x,rhs(eq)));T0_:=subs(sol,T0)*K_;'T0'=TKC(%);TL1_:=evalf(subs(x=Lt*(1-f),eqm_,dat,SI0,T1_))*K_;'TL1'=TKC(%);TL2_:=evalf(subs(x=-Lt*f,eqm_,dat,SI0,T2_))*K_;'TL2'=TKC(%);

i.e. la máxima es de 124 ºC en la resistencia, y las mínimas son de 22 ºC en el extremo más alejado, y de 42 ºC en el otro.

De los 24 W depositados, prácticamente van la mitad por cada lado, ya que las partes más alejadas apenas contribuyen a disipar calor.

>	plot([20,piecewise(x>0,T1_,T2_)-273],x=subs(dat,SI0,-Lt*f)..subs(dat,SI0,Lt*(1-f)),0..200,color=black);

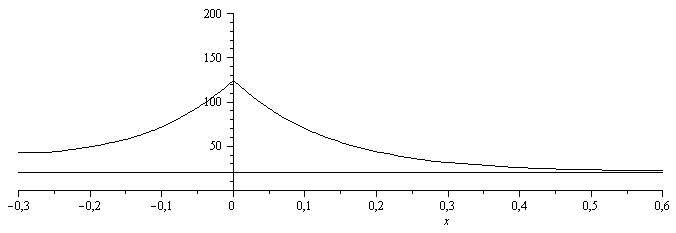Para comparación, se dibujan abajo la solución para el aluminio (4 veces más conductor), y para el acero inoxidable (3 veces menos conductor).

>