>	restart:#"m11_p67"

Un perfil de acero con forma de triángulo rectángulo cuyos catetos miden 2 y 4 cm, tiene 1 m de longitud, y una resistencia eléctrica de 20  y tamaño despreciable embebida a mitad de su longitud. Se quiere estudiar la transmisión de calor al ambiente, que está a 20 ºC y cuyo coeficiente convectivo se supone que es de 10 W/(m2•K), cuando se hace pasar una corriente eléctrica de 1 A por la resistencia (aislada eléctricamente). En particular, para el régimen estacionario, se pide:
a) Perfil esperado de temperatura a lo largo de la varilla.
b) Plantear el problema en forma diferencial (con las condiciones de contorno).
c) Temperaturas máxima y mínima.
d) Resolver el problema sabiendo que la solución para una varilla con temperatura fija en un extremo y libre en el otro es (TT)/(T0T)=cosh[m(Lx)]/cosh(mL).
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Acero":dat:=[Lt=1*m_,A=(0.02*0.04/2)*m_^2,p=(0.02+0.04+sqrt(0.02^2+0.04^2))*m_,Omega=20*ohm_,Tinf=(20+273.15)*K_,h=10*W_/(m_^2*K_),I=1*A_,Qt=20*W_];

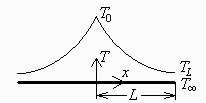
Eqs. const.:

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a) Perfil esperado de temperatura a lo largo de la varilla.

Basta resolver la mitad de la varilla, por simetría. Tomamos los ejes en el centro y llamamos L=Lt/2 (ver figura).

b) Plantear el problema en forma diferencial (con las condiciones de contorno).

Tomando un elemento genérico de longitud diferencial de varilla (desde x hasta x+dx), el balance energético es:

>	eq1:=subs(dA=0,epsilon=0,phi=0,eq11_12);eq1:=eq11_14;eqCC0:=Q0=-k*A*diff(T(x),x)[0];eqCCL:=diff(T(x),x)[L]=0;;eqm:=eq11_13;

La solución del problema es fácil, pero no es necesario hacerla porque viene en los libros de texto.

>	sol:=dsolve({subs(T[infinity]=Tinf,eq1),D(T)(0)=-Q0/(k*A),D(T)(L)=0},T(x));expand(convert(%,trig));

c) Temperaturas máxima y mínima.

La solución estacionaria con un flujo dado en un extremo y el otro libre es:

>

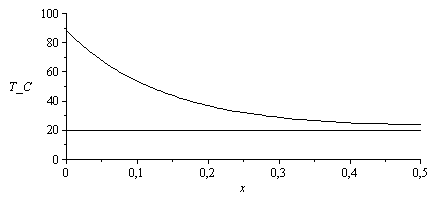
eq1:=T(x)=Tinf+(Q0/sqrt(p*h*k*A))*cosh(m*(L-x))/sinh(m*L);eqm_:=evalf(subs(dat,eqm));eq1_:=evalf(subs(Q0=Qt/2,L=Lt/2,eqm_,dat,SI0,eq1));T0_:=evalf(subs(x=0,rhs(eq1_)))*K_;'T0'=TKC(%);TL_:=evalf(subs(x=Lt/2,dat,SI0,rhs(eq1_)))*K_;'TL'=TKC(%);plot([subs(dat,SI0,Tinf)-273,rhs(eq1_)-273],x=0..subs(dat,SI0,Lt/2),T_C=0..100,color=black);

d) Resolver el problema sabiendo que la solución para una varilla con temperatura fija en un extremo y libre en el otro es (TT)/(T0T)=cosh[m(Lx)]/cosh(mL).

Si sólo se dispone de la solución de T0 dada, se haría así:

>	eq2:=T(x)=Tinf+(T0-Tinf)*cosh(m*(L-x))/cosh(m*L);eq0:=Q0=-k*A*diff(T(x),x)[0];eq0:=Q0=subs(x=0,-k*A*diff(rhs(eq2),x));T0_:=evalf(subs(eqm_,L=Lt/2,Q0=Qt/2,dat,SI0,solve(%,T0)))*K_;TL_:=evalf(subs(T0=T0_,x=L,L=Lt/2,eqm_,dat,SI0,rhs(eq2)))*K_;'TL'=TKC(%);

>