>	restart:#"m11_p65"

Se tiene un bloque de hierro de 5 cm de espesor, inicialmente en estado estacionario con una de sus caras a 50 ºC y la otra a 100 ºC. A partir de un cierto instante se aíslan térmicamente ambas caras, y se deja que el bloque se equilibre. Se pide:
a) Hacer un esquema del perfil de temperatura interior, en el instante inicial, en uno intermedio, y al final.
b) Calcular el calor que fluye por unidad de área en el instante inicial, y hacer un esquema del flujo de calor en un instante intermedio (i.e. variación espacial).
c) Estimar el tiempo de relajación, indicando en qué se basa.
d) Se va a modelizar el proceso de relajación por la función T(x,t)=T0+c1sin(x/L)exp(c2t); determinar las constantes T0, c1 y c2 que mejor se ajustan al problema.
e) Comparar el modelo anterior con el de variables separadas completo (i.e. T(x,t)=X(x)Y(t) con las ecuaciones diferenciales y condiciones iniciales y de contorno completas).

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(n,integer,N,integer,L>0):

>	su:="Hierro_fundido":dat:=[L=0.05*m_,T1=(100+273)*K_,T2=(50+273)*K_];

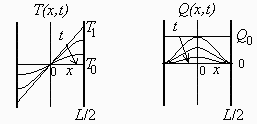
Eqs. const.:

>	dat:=op(dat),get_sol_data(su),Const,SI2,SI1:k=subs(dat,k);eqT:=T(x,t)=T0+c1*sin(Pi*x/L)*exp(-c2*t); dat:=op(subs(T0=T00,[dat])):

a) Hacer un esquema del perfil de temperatura interior, en el instante inicial, en uno intermedio, y al final.

(Ver figura)

b) Calcular el calor que fluye por unidad de área en el instante inicial, y hacer un esquema del flujo de calor en un instante intermedio (i.e. variación espacial).

Inicialmente el flujo de calor es uniforme en cada sección, i.e. q(x,0)=cte, y de valor:

>	eqQ:=Q/A=-k*(T1-T2)/L;eqQ_:=subs(dat,%);Tgrad:=(T1-T2)/L;Tgrad_:=subs(dat,%);

i.e. inicialmente fluyen 50 kW/m2 (el gradiente térmico es de 1 kW/m).

c) Estimar el tiempo de relajación.

Un análisis de órdenes de magnitud de la ecuación del calor enseña que:

>	eqC:=diff(T(x,t),t)/a=diff(T(x,t),x,x);eqt:=t[char]=L[char]^2/a;eqa:=a=k/(rho*c);eqa_:=subs(dat,%);eqt_:=subs(eqa_,L[char]=L/2,dat,eqt);

i.e., hacen falata unos 40 s para que la temperatura se aproxime al nuevo estado estacionario. Nótese que se ha tomado L/2 como longitud característica por ser el problema simétrico (o, lo que es lo mismo, el cociente entre el volumen y el área bañada).

d) Se va a modelizar el proceso de relajación por la función T(x,t)=T0+c1sin(x/L)exp(-c2t); determinar las constantes T0, c1 y c2 que mejor se ajustan al problema.

Como T(0,t)=T0, vemos que T0 es la temperatura en el origen, es decir, la media (por el balance energético). Vemos que se satisface automáticamente la condición de adiabaticidad en x=L/2, y que para t=infinito T(x,tinf)=T0, que es el estado final, así que hay que ajustar dos constantes para el problema. Como es imposible ajustar la condición inicial de perfil lineal de temperaturas, ajustamos sólo la ecuación del calor y la pendiente inicial en el origen (el flujo de calor inicial, y no la temperatura en el extremo, por ejemplo; ver figura comparativa).

>

eq0:=T(x,t)[x=0]=T0;eq0:=T0=(T1+T2)/2;subs(dat,%);plot(subs(T0=(T1+T2)/2-273,dat,SI0,[T0+(T1-T2)*x/L,T0+25*sin(Pi*x/L),T0+16*sin(Pi*x/L)]),x=-subs(dat,SI0,L/2)..subs(dat,SI0,L/2),T_C=50..100,color=black);eq1:=Diff(T(x,t),x)[x=L/2]=0;eq3:=Diff(T(x,t),x)[x=0,t=0]=Q/(k*A);eq3_:=eval(subs(x=0,t=0,diff(rhs(eqT),x)))=-rhs(eqQ)/k;c1_:=solve(%,c1);c1__:=evalf(subs(dat,%));eq4:=eqC;eq4_:=eval(subs(eqT,eq4));c2_:=solve(%,c2);c2__:=evalf(subs(eqa,dat,c2_));eqT_:=subs(c1=c1_,c2=c2_,eqT);

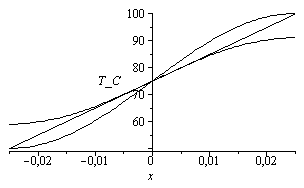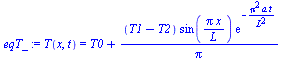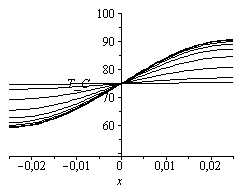
Puede verse el proceso de relajación en los diagramas siguientes: T(x,t),T(L/2,t),T'(0,t).

>	eqT_:=evalf(subs(c1=c1_,c2=c2__,T0=(T1+T2)/2,dat,SI0,eqT));plot([seq(subs(t=2^i,rhs(eqT_)-273),i=-2..6)],x=-subs(dat,SI0,L/2)..subs(dat,SI0,L/2),T_C=50..100,color=black);plot(subs(x=L/2,dat,SI0,rhs(eqT_)-273),t=0..100,T_C=75..100);

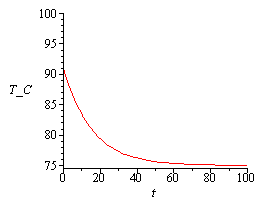Como se ve, a los 40 s, la cara que estaba a 100 ºC ha pasado a unos 76 ºC, prácticamente el valor final de 75 ºC.

e) Comparar el modelo anterior con el de variables separadas completo (i.e. T(x,t)=X(x)Y(t) con las ecuaciones diferenciales y condiciones iniciales y de contorno completas).

Sea DT=T(x,t)-Tfinal

>	pdeq:=subs(m=0,diff(DT(x,t),t)/a=diff(DT(x,t),x,x)-m^2*DT(x,t));sepvar:=DT(x,t)=X(x)*T(t);pdeq_:=expand(eval(subs(sepvar,pdeq/DT(x,t))));

Como hay simetría central (antisimetría), resolvemos 0<x<L/2 desarrollando en senos porque X(x=0)=0.

>	eqX:=X(x)=sin(an*x);eqT:=T(t)=exp(-bn*t);pdeq__:=eval(subs(eqX,eqT,pdeq_));eqb:=bn=solve(%,bn);sol1:=subs(eqX,eqT,eqb,sepvar);eqCheckPDE:=simplify(expand(subs(sol1,pdeq))):'eqCheckPDE'=rhs(%)-lhs(%);sgen:=subs(eqb,Sum(cn*rhs(eqX)*rhs(eqT),n=0..N));

Imponemos las condiciones iniciales y de contorno.

>	BC0:=DT[x=0]=0;BC1:=Diff(DT,x)[x=L/2]=0;BC0:=eval(subs(x=0,sgen))=0;BC1:=eval(subs(x=L/2,diff(sgen,x)))=0;

Para que se cumpla BC1 hace falta que an*L/2=Pi/2+n*Pi. Comprobamos que los términos son ortogonales, y construimos la condición inicial.

>

eqBC1:=an=(2*n+1)*Pi/L;eqX:=subs(eqBC1,eqX);eqOrt0:=Int(rhs(eqX)*subs(n=N,rhs(eqX)),x=0..L/2)=int(rhs(eqX)*subs(n=N,rhs(eqX)),x=0..L/2);eqOrt1:=Int(rhs(eqX)^2,x=0..L/2)=int(rhs(eqX)^2,x=0..L/2);IC:=DT[t=0]=DT1*x/(L/2);IC:=eval(subs(t=0,sgen))=DT1*x/(L/2);ICn:=cn*rhs(eqX)=DT1*x/(L/2);DT1_:=T[L/2]-T[0];DT1_:=subs(dat,T1-(T1+T2)/2);

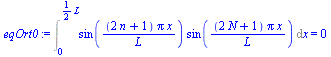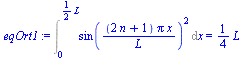Resolvemos la ecuación que determina cada coeficiente por separado (por ser ortogonales).

>	eqICn:=eval(int(lhs(ICn)*rhs(eqX),x=0..L/2))=int(rhs(eqX)*DT1*x/(L/2),x=0..L/2);cn_:=solve(%,cn);DT:=subs(cn=cn_,eqBC1,sgen);DT_1:=value(subs(N=0,DT));

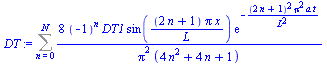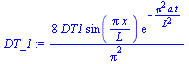Nótese que la única diferencia entre el modelo dado en el enunciado y el primer término del desarrollo, es que el coeficiente pasa de ser 1/Pi a ser 8/Pi^2.

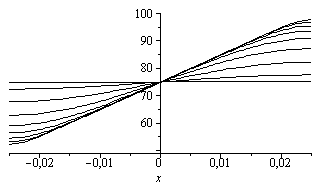
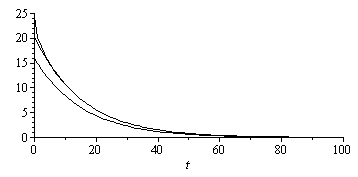
La representación gráfica para N=10 (11 términos) es:

>

DT_1_:=evalf(subs(DT1=DT1_,eqa,dat,SI0,DT_1));DT_10_:=evalf(subs(N=10,DT1=DT1_,eqa,dat,SI0,DT));plot([seq(subs(eq0,dat,SI0,t=2^i,T0+DT_10_-273),i=-2..6)],x=-subs(dat,SI0,L/2)..subs(dat,SI0,L/2),50..100,color=black);plot(subs(x=L/2,dat,SI0,[DT_1_,DT_10_,rhs(eqT_)-273-75]),t=0..1e2,0..25,color=black);plot(subs(x=0,[diff(DT_1_,x),diff(DT_10_,x),diff(rhs(eqT_),x)]),t=0..1e2,0..1000,color=black);

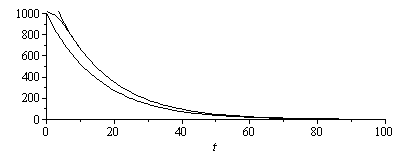Vemos, además, que el ajuste óptimo con un solo término no era con c1=16 ºC (ajuste de la pendiente en el origen) ni con c1=25 ºC (ajuste de la función en el extremo), sino con c1=20 ºC.

>