>	estart:#"m11_p62

Se trata de estimar la temperatura que tendrá una cubierta de caña que protege del sol en un área de descanso. Para ello, se va a suponer que el cañizo tiene un espesor medio de 3 mm y absorbe la mitad de la radiación solar, que a mediodía será del orden de 1 kW/m2, que el aire ambiente estará a unos 40 ºC y que el coeficiente convectivo será de unos 10 W/(m2•K). Se pide:
a) Hacer un esquema representativo de los flujos de calor involucrados, y resolver el problema despreciando las pérdidas radiativas y suponiendo que la temperatura del cañizo fuera uniforme.
b) Enumerar incógnitas y datos, y plantear las ecuaciones para resolver el problema térmico.
c) Resolver el problema anterior despreciando las pérdidas radiativas.
d) Incluir el efecto de las pérdidas radiativas.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	dat:=[alpha=0.5,E=1000*W_/m_^2,T0=(40+273.15)*K_,h=10*W_/(m_^2*K_),L=0.003*m_,k=0.1*W_/(m_*K_),epsilon=1];

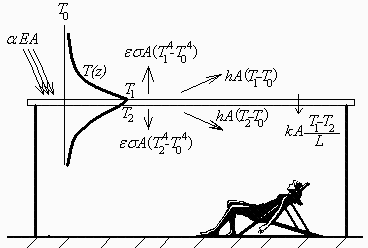
Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Hacer un esquema representativo de los flujos de calor involucrados, y resolver el problema despreciando las pérdidas radiativas y suponiendo que la temperatura del cañizo fuera uniforme.

El esquema de flujos y el perfil de temperaturas se han dibujado en la figura: hay una entrada (la solar) y unas salidas al entorno, por convección al aire y por radiación a elementos más lejanos (e.g. al suelo), además de una transmisión interna de la cara superior a la inferior.

Se supone que la temperatura del aire es la misma al sol que a la sombra, debido a que el aire se moverá si hay gradientes, que los habrá porque el suelo a la sombra estará menos caliente que el suelo al sol. De todas formas, se recuerda que la temperatura del aire siempre debe medirse con un termómetro protegido del sol y otras radiaciones (la temperatura en un ambiente que no esté en equilibrio depende de los mecanismos de transmisión de calor involucrados).

Sea T la temperatura buscada con el modelo de temperatura uniforme (que aproximaría el caso de poca resistencia térmica del cañizo).

>	eqBE0:=0=alpha*E-2*h*(T-T0)-2*epsilon*sigma*(T^4-T0^4);subs(epsilon=0,%);T_:=subs(dat,solve(subs(epsilon=0,dat,%),T));T=TKC(%);

i.e. el cañizo estaría a 65 ºC (con una temperatura del aire de 40 ºC).

Si, en lugar de despreciar la resistencia térmica del cañizo (por su pequeño espesor) la considerásemos infinita (por la baja conductividad térmica de la celulosa), el balance hubiera sido alpha*E-h*DT=0 y entonces el cañizo quedaría a 90 ºC por la parte de arriba y a 40 ºC por la de abajo.

>	eqBE0_:=0=alpha*E-h*(T-T0);T_:=subs(dat,solve(subs(epsilon=0,dat,%),T));T=TKC(%);

b) Enumerar incógnitas y datos, y plantear las ecuaciones para resolver el problema térmico.

Incógnitas: T1 y T2. Ecuaciones: los dos balances energéticos interfaciales.

La conductividad térmica representativa puede variar bastante según el tipo de cañizo, pues no se trata de un material leñoso macizo como la madera (k=0,15 W/(m·K)), sino que por el efecto de la porosidad del ensamblaje será algo menor. Tomemos k=0,1 W/(m·K) como órden de magnitud..

>	eqBE:=dE/dt=Qdot+Wdot;eqBE:=0=Qdot_net;eqBE1:=0=alpha*E-h*(T1-T0)-epsilon*sigma*(T1^4-T0^4)-k*(T1-T2)/L;eqBE2:=0=k*(T1-T2)/L-h*(T2-T0)-epsilon*sigma*(T2^4-T0^4);

c) Resolver el problema anterior despreciando las pérdidas radiativas.

Ahora será una variación lineal decreciente desde T1 a T2, que se determinan así:

>	eqs:=subs(epsilon=0,{eqBE1,eqBE2});sol_:=subs(dat,solve(eqs,{T1,T2}));

i.e., en lugar de los 65 ºC de media, la resistencia térmica del cañizo haría que hubiese 68 ºC por arriba y 61 ºC por abajo.

d) Incluir el efecto de las pérdidas radiativas.

Supondremos que el sombrajo intercambia calor por radiación con el suelo y el cielo, que los supondremos cuerpos negros a la temperatura ambiente. Tomamos también epsilon=1 para el sombrajo.

>	eqBE0;sol12_:=fsolve(subs(dat,SI0,%),T)[2]*K_;eqs:={eqBE1,eqBE2};sol_:=fsolve(subs(dat,SI0,%),{T1,T2})*K_;

i.e., teniendo en cuenta las pérdidas radiativas, queda en 57 ºC por arriba y 51 ºC por abajo.

Si no estuviera el sombrajo, la temperatura de lo que hay debajo aumentaría (la del suelo, si no hay otra cosa), y en lugar de ser de 40 ºC (algo mayor por la radiación que se recibe del sombrajo), sería casi la del sombrajo (por ejemplo, no se podría andar descalzo sin quemarse).

El sombrajo de cañizo, de caña entera o en tiras (que sería este caso, a la vista del pequeño espesor), ha sido el más usado en climas mediterráneos, aunque el sombrajo de brezo seco es más tupido y aisla más. La mejor sombra es la de un buen árbol (y es natural), pero es raro encontrar grandes árboles de sombra en esas regiones (y en medio estará el tronco), así que hay que hacer sombrajos artificiales, sea guiando arbustos vivos en un entramado artificial (emparrados y pérgolas), o disponiendo materia vegetal seca sobre un estructuras artificiales, que es hoy día lo más corriente.

>