>	restart:#"m11_p61"

Considérese una varilla de aluminio de 5 mm de radio y 0,5 m de longitud, por uno de cuyos extremos entra un flujo de calor de 5 W, en régimen estacionario, estando el resto rodeado de un fluido a 15 ºC con el que se estima un coeficiente convectivo de 10 W/(m2•K). Se quiere estudiar el efecto de ponerle una funda radial de 5 mm de espesor de corcho a toda la varilla. Se pide:
a) Hacer un esquema de los perfiles axial y radial de temperaturas esperadas.
b) Determinar las temperaturas extremas suponiendo que la funda fuese totalmente aislante.
c) Determinar las temperaturas extremas suponiendo que no hubiese funda.
d) Plantear la ecuación diferencial y las condiciones de contorno para el perfil de temperaturas en la varilla con su funda (despreciando la conducción axial en la funda)..
e) Calcular las temperaturas máxima y mínima en esa configuración.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):h:='h':

>	su1:="Aluminio_anodizado":su2:="Corcho":dat:=[R=0.005*m_,L=0.5*m_,Q0=5*W_,Tinf=(15+273)*K_,h=10*W_/(m_^2*K_),DR=5e-3*m_];

Eqs. const.:

>	sAdat:=get_sol_data(su1):sCdat:=get_sol_data(su2):dat:=op(dat),Const,SI2,SI1:k_Al=subs(sAdat,k);k_C=subs(sCdat,k);dat:=op(subs(T0=T[0],[dat])):

a) Hacer un esquema de los perfiles axial y radial de temperaturas esperadas.

(Hecho arriba)

b) Determinar las temperaturas extremas suponiendo que la funda fuese totalmente aislante.

Si no hubiese pérdidas laterales, en el régimen estacionario el perfíl axial de temperaturas sería lineal a lo largo de la varilla, y bastaría considerar la conducción a lo largo del alma de aluminio.

>

eqCalor:=diff(T(x),x,x)=0;eqCC1:=Q0=-k*A*diff(T(x),x)[x=0];eqCC2:=-k*A*diff(T(x),x)[x=L]=h*A*(T(x)-Tinf)[x=L];eqA:=A=Pi*R^2;eq0:=Q0=k*A*(T0-TL)/L;eqL:=k*A*(T0-TL)/L=h*A*(TL-Tinf);sol0:=expand(solve({eq0,eqL},{T0,TL}));DT:=expand(subs(%,T0-TL));sol0_:=subs(dat,evalf(subs(eqA,sAdat,dat,sol0)));DT_:=subs(%,T0-TL);

i.e. temperaturas inadmisiblemente altas. La explicación es que la convección al aire sólo por el extremo de la varilla de aluminio es muy poco eficiente, así que, pese a la baja conductividad del corcho, las pérdidas laterales son las importantes.

c) Determinar las temperaturas extremas suponiendo que no hubiese funda.

>

eqBE:=0=-k*A*diff(T(x),x)+k*A*(diff(T(x),x)+diff(T(x),x,x)*dx)+h*p*dx*(Tinf-T(x));eqDif:=diff(T(x),x,x)=m^2*(T(x)-Tinf);eqm:=m=sqrt(2*Pi*R*h/(k*Pi*R^2));evalf(subs(sAdat,dat,%));eqCC1:=Q0=-k*A*diff(T(x),x)[x=0];eqCC2:=0=-k*A*diff(T(x),x)[x=L];sol1:=dsolve({eqDif,D(T)(0)=-Q0/(k*A),D(T)(L)=0},T(x));sol1_:=evalf(subs(eqm,eqA,sAdat,dat,SI0,sol1));sol1book:=T(x)=Tinf+(Q0/sqrt(h*2*Pi*R*k*Pi*R^2))*cosh(m*(L-x))/sinh(m*L);[T0,TL]=evalf(subs(x=0,eqm,eqA,sAdat,dat,SI0,evalf([subs(x=0,rhs(sol1book)),subs(x=L,rhs(sol1book))])))*K_;

La solución sol1book viene directamente en algunos libros de Transmisión de Calor. También se podría haber usado la de la aleta canónica que viene en todos los libros (temperatura dada en la raiz, en vez del flujo), y obtener la temperatura en la raiz a partir del flujo en la raiz.

d) Plantear la ecuación diferencial y las condiciones de contorno para el perfil de temperaturas en la varilla con su funda (despreciando la conducción axial en la funda)..

>

eqBE_axial:=0=-k*A*diff(T(x),x)+k*A*(diff(T(x),x)+diff(T(x),x,x)*dx)+Q_L(x)*dx;Q_L(x):=h*p*(Tinf-Te(x));eqBE_radial:=2*Pi*kB*(T(x)-Te(x))/ln((R+DR)/R)=2*Pi*(R+DR)*h*(Te(x)-Tinf);Te_:=solve(eqBE_radial,Te(x));eqBE_axial:=diff(T(x),x,x)=simplify(m^2*(Te_-Tinf));eqm:=m=sqrt(h*p/(k*A));eqp:=p=2*Pi*(R+DR);eqA;evalf(subs(eqp,eqA,sAdat,dat,eqm));

e) Calcular las temperaturas máxima y mínima en esa configuración.

>	sol2_:=evalf(dsolve(evalf(subs(eqm,eqA,eqp,dat,sAdat,kB=k,sCdat,dat,SI0,{eqBE_axial,D(T)(0)=-Q0/(k*A),D(T)(L)=0})),T(x)));[T0,TL]=evalf([subs(x=0,rhs(sol2_)),subs(x=L,dat,SI0,rhs(sol2_))])*K_;

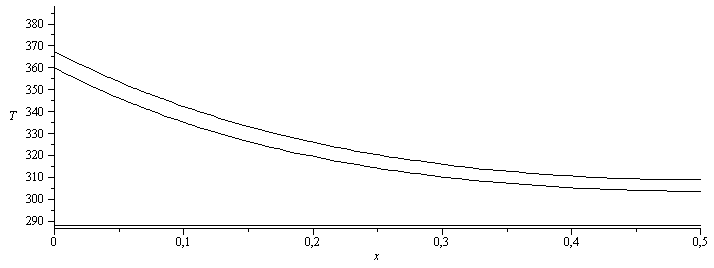
¡Vaya!, pues no era tan importante el aislante de corcho, y es que, el aire aisla tanto, que el corcho apenas influye. Incluso podría haber aumentado el enfriamiento si el radio de la varilla hubiese sido más pequeño (radio crítico rcr=k/h=0,05/10=5 mm).

>	plot(subs(eqm,dat,SI0,[[[0,Tinf],[L,Tinf]],rhs(sol2_),rhs(sol1_)]),x=0..subs(dat,SI0,L),T=288..388,color=black);

>