>	restart:#"m11_p60"

Considérese una lámina de cobre de 1•20•400 mm3 inicialmente a 300 K. A partir de un instante dado, se obliga a que las bases de 1•20 mm2 se mantengan a 400 K, mientras el resto sigue en contacto con aire ambiente a 300 K con el que puede suponerse un coeficiente convectivo de 20 W/(m2•K). Se pide:
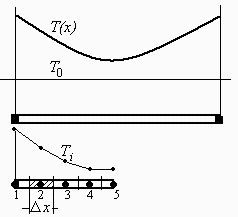
a) Hacer un esquema del campo de temperaturas esperado.
b) Plantear las ecuaciones diferenciales que determinan el perfil de temperatura en régimen estacionario.
c) Tómense elementos de 1•20•50 mm3 y, por el método de diferencias finitas, asígnense los nodos apropiados, estableciendo los balances energéticos nodales.
d) Determinar por diferencias finitas la evolución térmica.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="Cobre":dat:=[L1=0.001*m_,L2=0.02*m_,L3=0.4*m_,T1=400*K_,Tinf=300*K_,h=20*W_/(m_^2*K_),Dx=0.05*m_];

Eqs. const.:

>	dat:=op(dat),get_sol_data(su),Const,SI2,SI1:k=subs(dat,k);

a) Hacer un esquema del campo de temperaturas esperado.

Hecho arriba.

b) Plantear las ecuaciones diferenciales que determinan el perfil de temperatura en régimen estacionario.

Como el problema es simétrico, basta resolver una mitad, y elegimos la mitad izquierda.

>	eqL:=L=L3/2;deq:=diff(T(x),x,x)-m^2*(T(x)-Tinf)=0;eqm:=m=sqrt(h*p/(k*A));eqCC1:=T(0)=T0;eqCC2:=diff(T(x),x)[L]=0;

Se sabe que la solución de ese problema es:

>	Sol:=T(x)=Tinf+(T1-Tinf)*cosh(m*(L-x))/cosh(m*L);p=2*(L1+L2),A=L1*L2;eqm_:=evalf(subs(p=2*(L1+L2),A=L1*L2,dat,eqm));Tstdy_:=subs(eqL,eqm_,dat,SI0,rhs(Sol));plot(Tstdy_,x=0..subs(eqL,dat,SI0,L),T=subs(dat,SI0,Tinf)..subs(dat,SI0,T1));TL_:=evalf(subs(x=L,eqL,eqm_,dat,SI0,rhs(Sol)))*K_;

c) Tómense elementos de 1•20•50 mm3 y, por el método de diferencias finitas, asígnense los nodos apropiados, estableciendo los balances energéticos nodales.

Como L=L3/2=20 cm y dicen que tomemos elementos de 5 cm, habrá N=5 nodos, que numeramos i=1,2,3,4,5 (ver figura arriba).

El Dt apropiado se determina con el criterio de estabilidad, y el número de iteraciones necesarias con un criterio de convergencia ad hoc, o estimando previamente el tiempo de relajación.

>	deq:=diff(T(x,t),t)=a*(diff(T(x),x,x)-m^2*(T(x)-Tinf));deq_dis:=(T[j+1,i]-T[j,i])/Dt=a*((T[j,i-1]-2*T[j,i]+T[j,i+1])/Dx^2-m^2*(T[j,i]-Tinf));deq_dis:=T[j+1,i]-T[j,i]=a*Dt*(T[j,i-1]-2*T[j,i]+T[j,i+1])/Dx^2-a*Dt*m^2*(T[j,i]-Tinf);eqFo:=Fo=a*Dt/Dx^2;eqBi:=Bi=m^2*Dx^2;eqFo_max:=Fo*(1+Bi)=1/2;

>

Dx_:=subs(dat,Dx);N:=L/Dx+1;N_:=subs(eqL,dat,%);N_:=5;N:='N':eqm_;Bi_:=subs(eqm_,Dx=Dx_,rhs(eqBi));Fo_:=subs(Bi=Bi_,solve(eqFo_max,Fo));Dt_:=subs(dat,Fo_*rho*c*Dx_^2/k);eqNodo1:=T[j+1,i]=T1;eqNodo2ysucesivos:=T[j+1,i]=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])-Fo*'Bi'*(T[j,i]-Tinf);eqNodoN_aislado:=T[j+1,N]=T[j+1,N-1];M_:=20;T_:=array(1..M_,1..N_);for j from 1 to M_ do T_[j,1]:=subs(dat,SI0,T1);for i from 2 to N_ do T_[j,i]:=subs(dat,SI0,Tinf) end do:end do:#print(T_);

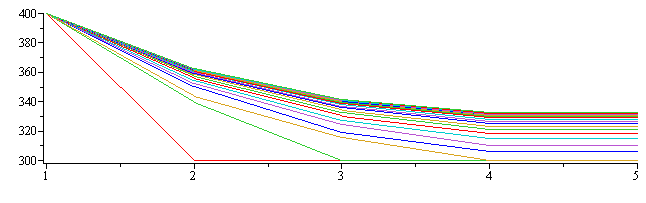
d) Determinar por diferencias finitas la evolución térmica.

Iterando:

>

for j from 1 to M_-1 do T_[j+1,1]:=T_[j,1];for i from 2 to N_-1 do  T_[j+1,i]:=T_[j,i]+Fo_*(T_[j,i-1]-2*T_[j,i]+T_[j,i+1])-Fo_*Bi_*(T_[j,i]-subs(dat,SI0,Tinf)) end do: i:=N_;T_[j+1,i]:=T_[j+1,i-1];end do:print(T_);l1:=[seq([seq([i,T_[j,i]],i=1..N_)],j=1..M_)]:plot(l1);l1_:=seq([seq([(i-1)*subs(SI0,Dx_),T_[j,i]],i=1..N_)],j=1..M_):plot({l1_[M_],Tstdy_},x=0..subs(eqL,dat,SI0,L),Temp=subs(dat,SI0,Tinf)..subs(dat,SI0,T1),color=black);l1_:=[seq(seq([j*subs(SI0,Dt_),T_[j,i]],i=N_..N_),j=1..M_)]:plot([[[0,subs(SI0,TL_)],[200,subs(SI0,TL_)]],l1_],Time_s=0..200);

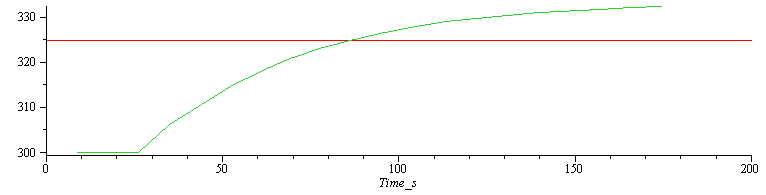No estaba mal esa aproximación, aunque la temperatura que se alcanza en el extremo es casi un 30% mayor que el salto esperado (la solución teórica estacionaria).

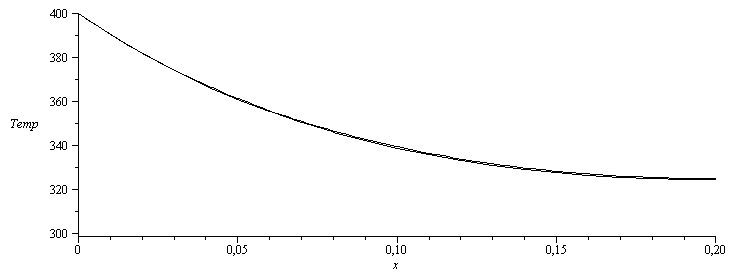
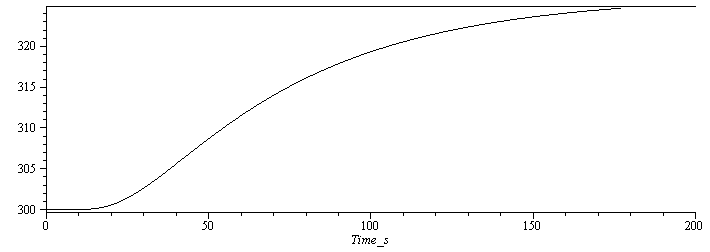
ADICIONAL. Si tomásemos elementos de 1 cm en vez de de 5 cm, la aproximación es ya excelente.

>

Dx_:=subs(dat,Dx/5);N_:=21;M_:=500;Fo_:=0.4;Dt_:=subs(dat,Fo_*rho*c*Dx_^2/k);Bi:=p*h*Dx^2/(k*A);Bi:=2*(L1+L2)*h*Dx_^2/(k*L1*L2);Bi_:=subs(N=N_,Fo=Fo_,dat,Bi);eqNodo1:=T[j+1,i]=T1;eqNodo2ysucesivos:=T[j+1,i]=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])-Fo*'Bi'*(T[j,i]-Tinf);eqNodoN_aislado:=T[j+1,N]=T[j+1,N-1];T_:=array(1..M_,1..N_);Digits:=10:for j from 1 to M_ do T_[j,1]:=subs(dat,SI0,T1);for i from 2 to N_ do T_[j,i]:=subs(dat,SI0,Tinf) end do:end do:for j from 1 to M_-1 do T_[j+1,1]:=T_[j,1];for i from 2 to N_-1 do  T_[j+1,i]:=T_[j,i]+Fo_*(T_[j,i-1]-2*T_[j,i]+T_[j,i+1])-Fo_*Bi_*(T_[j,i]-subs(dat,SI0,Tinf)) end do: i:=N_;T_[j+1,i]:=T_[j+1,i-1];end do:l1:=[seq([seq([i,T_[j,i]],i=1..N_)],j=1..M_)]:plot(l1);l1_:=seq([seq([(i-1)*subs(SI0,Dx_),T_[j,i]],i=1..N_)],j=1..M_):plot({l1_[M_],Tstdy_},x=0..subs(eqL,dat,SI0,L),Temp=subs(dat,SI0,Tinf)..subs(dat,SI0,T1),color=black);l1_:=[seq(seq([j*subs(SI0,Dt_),T_[j,i]],i=N_..N_),j=1..M_)]:plot([[[0,subs(SI0,TL_)],[200,subs(SI0,TL_)]],l1_],Time_s=0..200,color=black);

>