>	restart:#"m11_p59"

Una lámina de aluminio de 1•20•400 mm3 en régimen estacionario, tiene una de las bases de 1•20 mm2 mantenida a 300 ºC, la otra a 100 ºC, y el resto en contacto con aire ambiente a 15 ºC con el que puede suponerse un coeficiente convectivo de 20 W/(m2•K). Se pide:
a) Hacer un esquema del campo de temperaturas esperado.
b) Plantear las ecuaciones que determinan el perfil de temperatura.
c) Ajustar con una función cuadrática el perfil de temperatura, y determinar el valor mínimo.
d) Sabiendo que la solución con un extremo empotrado y el otro libre es =cosh(m(Lx))/cosh(mL), resolver el problema por yuxtaposición de dos soluciones.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="Aluminio_anodizado":dat:=[L1=0.001*m_,L2=0.02*m_,L=0.4*m_,T0=(300+273.15)*K_,TL=(100+273.15)*K_,Tinf=(15+273.15)*K_,h=20*W_/(m_^2*K_)];

Eqs. const.:

>	dat:=op(dat),get_sol_data(su),Const,SI2,SI1:

a) Hacer un esquema del campo de temperaturas esperado.

Hecho arriba.

b) Plantear las ecuaciones que determinan el perfil de temperatura.

>	deq:=diff(T(x),x,x)-m^2*(T(x)-Tinf)=0;eqm:=m=sqrt(h*p/(k*A));eqCC1:=T(0)=T0;eqCC2:=T(L)=TL;

Solución:

>	sol:=dsolve({deq,eqCC1,eqCC2},T(x)):collect(%,{T0,TL,Tinf});simplify(convert(%,trig)):collect(%,{T0,TL,Tinf});eqm_:=subs(p=2*(L1+L2),A=L1*L2,dat,eqm);sol_:=evalf(subs(eqm_,dat,SI0,sol));plot([15,rhs(sol_)-273],x=0..0.4,T=0..300);Tmin=(minimize(subs(sol_,SI0,rhs(sol_)),x=0..0.4)-273)*ºC;

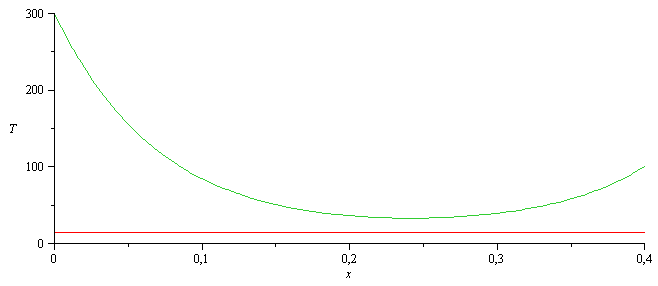c) Ajustar con una función cuadrática el perfil de temperatura, y determinar el valor mínimo.

Además de las dos condiciones de contorno, obligaremos a que se cumpla el balance energético global de la varilla: Qin=Qout.

>

Tc:=c0+c1*x+c2*x^2;eq1:=T0=subs(x=0,Tc);eq2:=TL=subs(x=L,Tc);eq3:=Qin=Qout;eq3:=-k*A*Diff('Tc',x)[x=0]+k*A*Diff('Tc',x)[x=L]=Int(h*p*(Tc-Tinf),x=0..L);eq3:=-subs(x=0,A=L1*L2,k*A*diff(Tc,x))+subs(x=L,A=L1*L2,k*A*diff(Tc,x))=int(h*2*(L1+L2)*(Tc-Tinf),x=0..L);solc:=solve({eq1,eq2,eq3},{c0,c1,c2});solc_:=subs(dat,solc);plot([rhs(sol_)-273,subs(solc_,eqm_,SI0,Tc)-273],x=0..0.4);Tcmin=(minimize(subs(solc_,SI0,Tc),x=0..0.4)-273)*ºC;

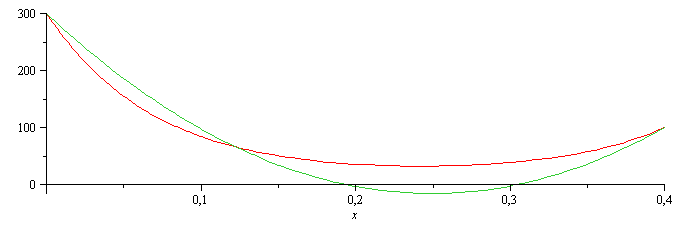Este ajuste no es aceptable porque daría una emperatura mínima inferior a la mínima del contorno (257<288). Probaremos con otro ajuste para el 3er coeficiente: que se verifique la equación del calor en el punto medio x=L/2.

>	Tn:=c0+c1*x+c2*x^2;eq1:=T0=subs(x=0,Tn);eq2:=TL=subs(x=L,Tn);eq3:=subs(x=L/2,diff(Tn,x,x)-m^2*(Tn-Tinf));soln:=solve({eq1,eq2,eq3},{c0,c1,c2});soln_:=subs(eqm_,dat,soln);plot([rhs(sol_)-273,subs(soln_,SI0,Tn)-273],x=0..0.4);Tnmin=(minimize(subs(soln_,SI0,Tn),x=0..0.4)-273)*ºC;

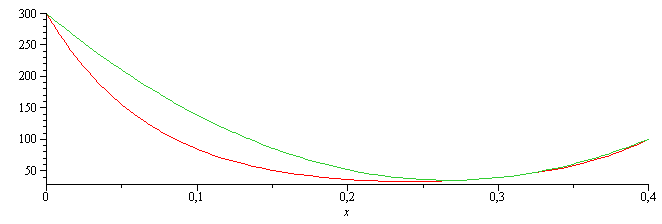i.e. la solución parece buena. Si no dispusiéramos de la solución exacta, podríamos compararla con un ajuste de más términos, e.g. 'colocando' la equación en x=0,L/3,2L/3,L:

>

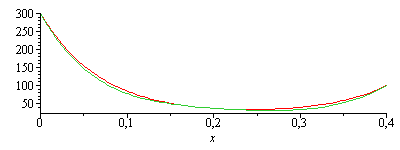
Tb:=c0+c1*x+c2*x^2+c3*x^3+c4*x^4+c5*x^5;eq1:=T0=subs(x=0,Tb);eq2:=TL=subs(x=L,Tb);eqC:=Diff('Tb',x,x)-m^2*('Tb'-Tinf)=0;eq3:=subs(x=0,value(eqC));eq4:=subs(x=L/3,value(eqC));eq5:=subs(x=2*L/3,value(eqC));eq6:=subs(x=L,value(eqC));solb_:=fsolve(subs(eqm_,dat,SI0,{eq1,eq2,eq3,eq4,eq5,eq6}),{c0,c1,c2,c3,c4,c5});plot([rhs(sol_)-273,subs(solb_,eqm_,SI0,Tb)-273],x=0..0.4);plot([diff(rhs(sol_),x,x),diff(subs(solb_,eqm_,SI0,Tb),x,x)],x=0..0.4);xTmin_:=fsolve(diff(subs(solb_,SI0,Tb),x)=0,x=0..0.4);Tmin_:=subs(x=xTmin_,solb_,SI0,Tb)*K_;Tbmin_=TKC(%);

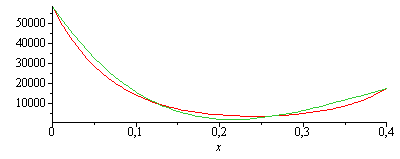luego, la aproximaciíon cuadrática anterior parece aceptable. Véanse las comparaciones con la solución exacta, así como el residuo de la ecuación del calor eneste último caso, para comprobar que se ha anulado en x=0,L/3,2L/3,L.

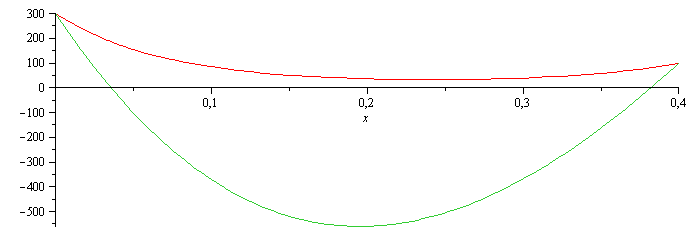
Hay que llevar cuidado con la elección de los puntos de ajuste, pues, si se hubiera ajustado sólo en los extremos, el resultado sería desastroso, como se ve a continuación:

>

Tb:=c0+c1*x+c2*x^2+c3*x^3;eq1:=T0=subs(x=0,Tb);eq2:=TL=subs(x=L,Tb);eqC:=Diff('Tb',x,x)-m^2*('Tb'-Tinf)=0;eq3:=subs(x=0,value(eqC));eq4:=subs(x=L,value(eqC));solb_:=fsolve(subs(eqm_,dat,SI0,{eq1,eq2,eq3,eq4}),{c0,c1,c2,c3});plot([rhs(sol_)-273,subs(solb_,eqm_,SI0,Tb)-273],x=0..0.4);plot([diff(rhs(sol_),x,x),diff(subs(solb_,eqm_,SI0,Tb),x,x)],x=0..0.4);Tbmin=(minimize(subs(solb_,SI0,Tb),x=0..0.4)-273)*ºC;

imposible, como se había anunciado.

d) Sabiendo que la solución con un extremo empotrado y el otro libre es =cosh(m(Lx))/cosh(mL), resolver el problema por yuxtaposición de dos soluciones.

Sea xm la posición del mínimo, de valor Tmin. Haciendo que ajuste por los dos lados:

>

eq11_15;eq:=T=Tinf+(T0-Tinf)*cosh(m*(L-x))/cosh(m*L);sol1:=subs(T=T1,L=xm,%);sol1_xm:=eval(subs(x=xm,%)):sol1_xm_:=evalf(subs(T1=Tmin,eqm_,dat,SI0,%)):sol2:=T2=Tinf+(TL-Tinf)*cosh(m*(L-xm-x))/cosh(m*(L-xm));sol2_xm:=eval(subs(x=L-xm,%)):sol2_xm_:=evalf(subs(T2=Tmin,eqm_,dat,SI0,%)):eqmatch:=rhs(sol1_xm_)=rhs(sol2_xm_);xm_:=fsolve(rhs(sol1_xm_)=rhs(sol2_xm_),xm=0..0.4);Tmin_:=(evalf(subs(xm=xm_,rhs(sol1_xm_)))-273)*ºC;plot([rhs(sol_)-273,subs(xm=xm_,eqm_,dat,SI0,rhs(sol1))-273,15],x=0..0.4,T=0..300,color=black);

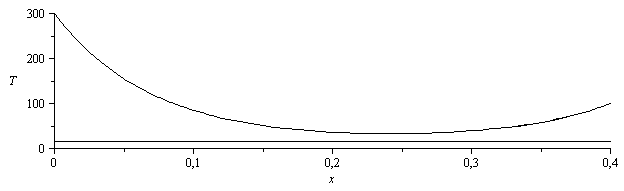Perfecto (nótese que basta con una función, pues es la misma por un lado que por el otro.

>