>	restart:#"m11_p58"

Considérese una plancha de madera de pino de 12 mm de espesor, expuesta al aire ambiente a 300 K con coeficiente convectivo h=15 W/(m2•K), que a partir de un cierto instante recibe una irradiancia de 1 kW/m2 por la cara superior.Se pide:

a) Determinar el estado térmico al que tiende.

b) Estimar el tiempo de relajación.

c) Calcular el proceso transitorio.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(Nx_,integer,Ny_,integer):

>	su:="Madera_de_pino":dat:=[L=0.012*m_,Tinf=300*K_,E=1e3*W_/m_^2,h=15*W_/(m_^2*K_)];

Eqs. const.:  

>	Sdat:=[get_sol_data(su)]:dat:=op(dat),Sdat,a=subs(Sdat,k/(rho*c)),Const,SI2,SI1:

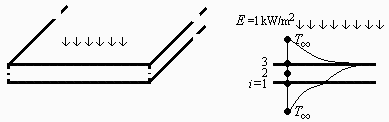
a) Determinar el estado térmico al que tiende.

En régimen estacionario, los balances energéticos en las interfases son:

>	eqBE1:=k*A*(T2-T1)/L=h*A*(T1-Tinf);eqBE2:=E*A=k*A*(T2-T1)/L+h*A*(T2-Tinf);sol:=subs(dat,solve({eqBE1,eqBE2},{T1,T2}));

i.e. la cara irradiada se calienta 45 ºC y la opuesta 20 ºC.

b) Estimar el tiempo de relajación.

Dependerá del número de Biot, i.e. si domina la conducción o la convección (aunque aquí el efecto forzador es radiativo

>	eqBi:=Bi=h*L/k;subs(dat,%);eqt_hinf:=t[r]=L^2/a;subs(dat,%);eqt_h0:=t[r]=rho*c*L/h;subs(dat,%);

i.e., si Bi>>1 (e.g. si se metiese en un baño agitado) tardaría unos 1100 s en reducir a la mitad su diferencia de temperatura, mientras que si Bi<<1 (e.g. si el sólido fuese muy buen conductor) tardaría unos 930 s. En este último caso, toda la madera estaría prácticamente a temperatura uniforme, y se podría calcular el régimen transitorio de una manera sencilla:

>	eqBEglobal:=rho*A*L*c*diff(Tg(t),t)=E*A-2*h*A*(Tg(t)-Tinf);sol:=dsolve({eqBEglobal,Tg(0)=Tinf},Tg(t));sol_:=subs(dat,SI0,%);Tg_stdy:=limit(%,t=+infinity):plot([rhs(Tg_stdy),rhs(sol_)],t=0..2000);

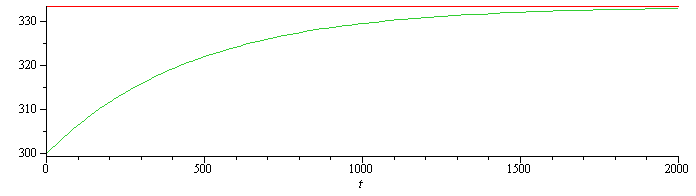pero no es de esperar que la madera, que tiene baja conductividad térmica, quede bien modelizada suponiendo Bi=hL/k<<1, así que habrá que usar al menos dos nodos (uno en cada cara). Usaremos el método de diferencias finitas, por ser el más sencillo.

c) Calcular el proceso transitorio.

Método de diferencias finitas con pocos nodos, para hacerlo a mano.

Aunque con dos nodos (uno en cada cara) ya tendríamos bien representado el problema, usaremos otro nodo intermedio para poder luego generalizar y añadir más.

>	eqDz:=Dz=L/2;subs(dat,%);eqBi:=Bi=h*Dz/k;subs(eqDz,dat,%);eqStab:=Fo*(1+Bi)<1/2;Fo_:=subs(eqBi,eqDz,dat,1/(2*(1+Bi)));Dt_:=subs(eqDz,dat,Fo_*Dz^2/a);FoBi_:=subs(eqBi,eqDz,dat,Fo_*Bi);N:=L/Dz+1;N_:=subs(eqDz,dat,%);M_:=2*N_^2;Tn:=array(1..M_,1..N_,[seq([seq(subs(dat,SI0,Tinf),i=1..N_)],j=1..M_)]):

Nodo 1.

>	eqBE1:=rho*A*(Dz/2)*c*(Tn[j+1,1]-Tn[j,1])/Dt=k*A*(Tn[j,2]-Tn[j,1])/Dz-h*A*(Tn[j,1]-Tinf);eqBE1:=Tn[j+1,1]=Tn[j,1]+2*Fo*(Tn[j,2]-Tn[j,1])-2*FoBi*(Tn[j,1]-Tinf);

Nodo 2 (genérico).

>	eqBE2:=rho*A*Dz*c*(Tn[j+1,i]-Tn[j,i])/Dt=k*A*(Tn[j,i+1]-Tn[j,i])/Dz;eqBE2:=Tn[j+1,i]=Tn[j,i]+Fo*(Tn[j,i-1]-2*Tn[j,1]+Tn[j,i+1]);

Nodo 3 (N).

>	N:='N':eqBE3:=rho*A*(Dz/2)*c*(Tn[j+1,N]-Tn[j,N])/Dt=k*A*(Tn[j,N-1]-T[nj,N])/Dz-h*A*(Tn[j,N]-Tinf-E/h);eqBE3:=Tn[j+1,N_]=Tn[j,N_]+2*Fo*(Tn[j,N_-1]-Tn[j,N_])-2*FoBi*(Tn[j,N_]-Tinf-E/h);

Iteraciones:

>

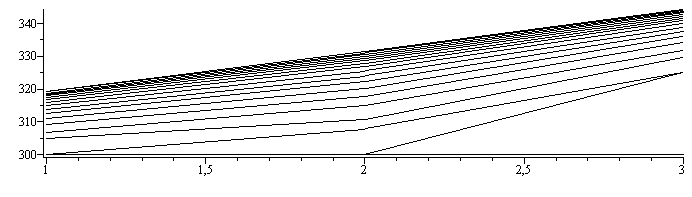
for j from 1 to M_-1 do j;Tn[j+1,N_]:=subs(N=N_,Fo=Fo_,FoBi=FoBi_,dat,SI0,Tn[j,N_]+2*Fo*(Tn[j,N_-1]-Tn[j,N_])-2*FoBi*(Tn[j,N_]-Tinf-E/h));for i from 2 to N_-1 do i,i;Tn[j+1,i]:=subs(N=N_,Fo=Fo_,FoBi=FoBi_,dat,SI0,Tn[j,i]+Fo*(Tn[j,i-1]-2*Tn[j,i]+Tn[j,i+1]));end do;Tn[j+1,1]:=subs(N=N_,Fo=Fo_,FoBi=FoBi_,dat,SI0,Tn[j,1]+2*Fo*(Tn[j,2]-Tn[j,1])-2*FoBi*(Tn[j,1]-Tinf));end do:s:=[seq([seq([i,Tn[j,i]],i=1..N_)],j=1..M_)]:plot(s,color=black);print(Tn);t[r]=Dt_*M_;

Con más elementos:

>

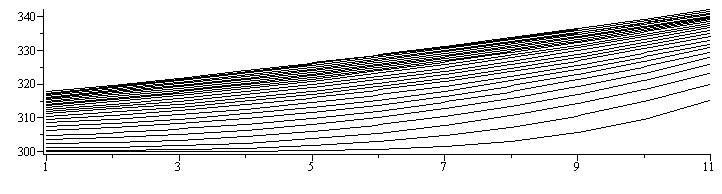
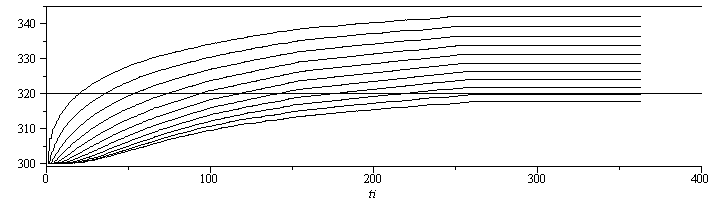
Nele:=10:eqDz:=Dz=L/Nele;subs(dat,%);eqBi:=Bi=h*Dz/k;subs(eqDz,dat,%);eqStab:=Fo*(1+Bi)<1/2;Fo_:=subs(eqBi,eqDz,dat,1/(2*(1+Bi)));Dt_:=subs(eqDz,dat,Fo_*Dz^2/a);FoBi_:=subs(eqBi,eqDz,dat,Fo_*Bi);N:=L/Dz+1;N_:=subs(eqDz,dat,%);M_:=3*N_^2;Tn:=array(1..M_,1..N_,[seq([seq(subs(dat,SI0,Tinf),i=1..N_)],j=1..M_)]):for j from 1 to M_-1 do j;Tn[j+1,N_]:=subs(N=N_,Fo=Fo_,FoBi=FoBi_,dat,SI0,Tn[j,N_]+2*Fo*(Tn[j,N_-1]-Tn[j,N_])-2*FoBi*(Tn[j,N_]-Tinf-E/h));for i from 2 to N_-1 do i,i;Tn[j+1,i]:=subs(N=N_,Fo=Fo_,FoBi=FoBi_,dat,SI0,Tn[j,i]+Fo*(Tn[j,i-1]-2*Tn[j,i]+Tn[j,i+1]));end do;Tn[j+1,1]:=subs(N=N_,Fo=Fo_,FoBi=FoBi_,dat,SI0,Tn[j,1]+2*Fo*(Tn[j,2]-Tn[j,1])-2*FoBi*(Tn[j,1]-Tinf));end do:s:=[seq([seq([i,Tn[jj*10,i]],i=1..N_)],jj=1..M_/10)]:plot(s,color=black);s:=[seq([seq([j,Tn[j,i]],j=1..M_)],i=1..N_)]:plot([320,345,op(s)],ti=0..400,color=black);t[r]=evalf(Dt_*M_,2);

>