>	restart:#"m11_p56"

Estimar el tiempo que tardaría en disolverse una burbuja de CO2 de 1 mm de diámetro en agua pura a presión atmosférica y 0 ºC (y a 50 ºC), sabiendo que la difusividad del CO2 en agua a 25 ºC es de 2,4109 m2/s y la solubilidad es ci,liq/ci,gas=1,8 a 0 ºC y 0,5 a 50 ºC.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="CO2":su2:="H2O":dat:=[D=1e-3*m_,T1=(0+273)*K_,T2=(50+273)*K_,Di25=2.4e-9*m_^2/s_,Kcc0=1.8,Kcc50=0.5];

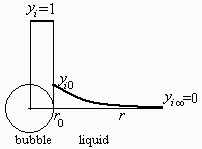
Eqs. const.:

>	Gdat:=get_gas_data(su1):Wdat:=get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:

>	eqmu:=eq12_7;eqFick:=eq11_34;eqDi:=D[i]=Di25*mu[water,25]/mu[water,T];eqSol:=c[i,liq]/c[i,gas]=Kcc;eqKcc:=Kcc=Kcc25*(mu[water,T]/mu[water,25])^1.5;

Variación de las propiedades con la T.

>	plot(subs(mu[water,T]=rhs(eqmu),mu[water,25]=subs(T=T25,rhs(eqmu)),dat,SI0,Kcc25=0.8,[rhs(eqDi)*1e9,rhs(eqKcc)]),T=273..323);

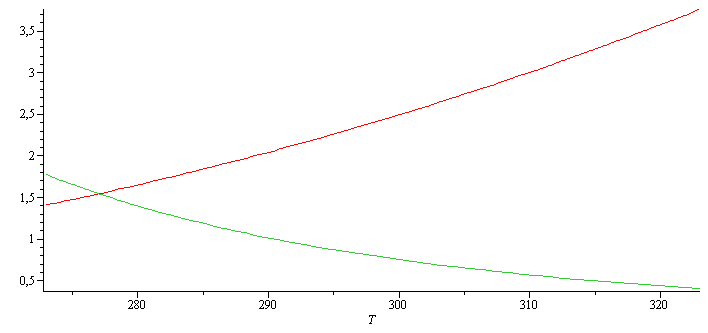a) Estimar el tiempo que tardaría en disolverse.

Una estimación de orden de magnitud sería t=L2/(Div*Dy) para la difusión de una gota de un líquido en otro líquido, y multiplicado por rho_gas/rho_liq sería para una 'gota de gas' en un líquido.

>

eqt1:=t[evap]=(r[0]^2/(Di*Dyi))*(rho[gas]/rho[liq]);eqETgas:=rho[gas]=subs(Gdat,dat,p0/(R*T0));eqETliq:=rho[liq]=subs(Wdat,rho);eqyi:=yi0=rho[i,liq]/rho[water];eqyi:=yi0=c[i,gas]*Kcc*M[i]/rho[water];eqyi:=yi0=(x[i,gas]*p/(R[u]*T))*Kcc*M/rho[water];T1=subs(dat,T1);eqyi_T1:=subs(x[i,gas]=1,Kcc=Kcc0,p=p0,T=T1,dat,Gdat,rho[water]=rho,Wdat,dat,eqyi);eqDi_T1:=Di=evalf(subs(mu[water,T]=subs(T=T1,rhs(eqmu)),mu[water,25]=subs(T=T25,rhs(eqmu)),dat,rhs(eqDi)));eqt_T1:=subs(r[0]=D/2,eqDi_T1,Dyi=rhs(eqyi_T1),eqETliq,eqETgas,eqyi,dat,eqt1);T2=subs(dat,T2);eqyi_T2:=subs(x[i,gas]=1,Kcc=Kcc0,p=p0,T=T2,dat,Gdat,rho[water]=rho,Wdat,dat,eqyi);eqDi_T2:=Di=evalf(subs(mu[water,T]=subs(T=T2,rhs(eqmu)),mu[water,25]=subs(T=T25,rhs(eqmu)),dat,rhs(eqDi)));eqt_T2:=subs(r[0]=D/2,eqDi_T2,Dyi=rhs(eqyi_T2),eqETliq,eqETgas,eqyi,dat,eqt1):evalf(%,2);

i.e., a 0 ºC tardaría unos 90 s y a 50 ºC unos 40 s.

Una estimación más precisa, sería aplicar la fórmula siguiente, lo que daría tiemopos mitad de los anteriores.

>

eqt2:=t[evap]=(r[0]^2/(2*Di*Dyi))*(rho[gas]/rho[liq]);eqyi_T:=subs(x[i,gas]=1,Kcc=Kcc0,p=p0,dat,Gdat,rho[water]=rho,Wdat,dat,eqyi);eqDi_T:=Di=evalf(subs(mu[water,T]=subs(T=T,rhs(eqmu)),mu[water,25]=subs(T=T25,rhs(eqmu)),dat,rhs(eqDi)));eqt_T:=subs(r[0]=D/2,eqDi_T,Dyi=rhs(eqyi_T),eqETliq,eqETgas,eqyi,dat,eqt2);plot(subs(SI0,rhs(%)),T=273..323,t=0..100);

>
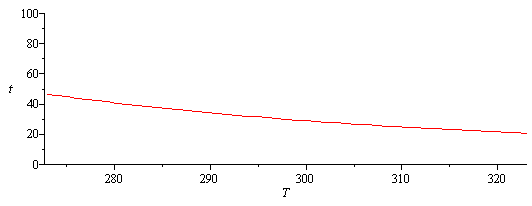