>	restart:#"m11_p50"

Un pequeño soporte tronco-cónico de cobre de 5 cm de longitud, une dos superficies metálicas, una a 300 K en contacto con la cara pequeña, que tiene 1 cm de diámetro, y la otra a 400 K en contacto con la cara grande, que tiene 3 cm de diámetro. Suponiendo flujo unidimensional, estacionario, y despreciando las pérdidas laterales, se pide:
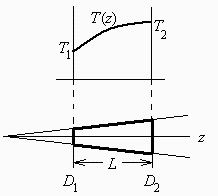
a) Hacer un esquema del perfil de temperatura esperado.
b) Plantear el balance energético de una rodaja infinitesimal de soporte.
c) Determinar la temperatura en la sección intermedia.
d) Determinar el flujo de calor a través del soporte.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0):

>	su:="Cobre":dat:=[L=0.05*m_,T1=300*K_,D1=0.01*m_,T2=400*K_,D2=0.03*m_];

>	dat:=op(dat),get_sol_data(su),Const,SI2,SI1:

a) Hacer un esquema del perfil de temperatura esperado.

Sería recto si fuese transmisión plana, pero como cada vez hay más área y el flujo total ha de mantenerse, la densidad de flujo irá disminuyendo, y por tanto la pendiente del perfil de temperaturas.

b) Plantear el balance energético de una rodaja infinitesimal de soporte.

>	eq11_4_1;eqBE:=0=Q(z)-Q(z+dz);eqFou:=Q(z)=-k*A(z)*diff(T(z),z);eqBE:=0=-k*A(z)*diff(T(z),z)+k*(A(z)+diff(A(z),z)*dz)*(diff(T(z),z)+diff(T(z),z,z)*dz);eqBE:=0=diff(A(z),z)*diff(T(z),z)+A(z)*diff(T(z),z,z);

c) Determinar la temperatura en la sección intermedia.

Tomando el origen de z como se indica en la figura, la ley de áreas es A(z)=K*z^2, luego la pendiente va como 1/z^2 y el perfil de T como 1/z.

>	eqA:=A(z)=Pi*(D1+(D2-D1)*z/L)^2/4;dsol:=dsolve([subs(eqA,eqBE),T(0)=T1,T(L)=T2],T(z));dsol_:=subs(dat,%);evalf(subs(z=L/2,dat,%));

Nótese que sale más de la media, como ya se había razonado.

d) Determinar el flujo de calor a través del soporte.

>	eqFou;eqFou:=simplify(subs(eval(subs(eqA,dsol,%))));subs(dat,evalf(subs(dat,%)));

i.e. fluyen 185 W hacia las z decrecientes. Nótese que no ha habido que particularizar la ecuación de Fourier porque Q no depende de z.

>

>