>	restart:#"m11_p49"

Una varilla de aluminio de sección cuadrada de 5 mm de lado y 1 m de longitud se mantiene con sus extremos a 600 K y 400 K respectivamente. La varilla tiene perfectamente aislados exteriormente los 25 cm finales del extremo más caliente, estando el resto de la varilla desnudo. El coeficiente convectivo con el aire circundante, que está a 300 K, se estima en 20 W/(m2•K). Asumiendo condiciones de flujo de calor unidimensional y régimen permanente, se pide:
a) Hacer y explicar un esquema del perfil de temperaturas esperado.
b) Calcular la temperatura de la sección transversal central del tramo aislado.
c) Calcular la temperatura de la sección transversal central de la varilla.
d) Calcular la temperatura superficial mínima de la varilla y la posición en que se produce.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Aluminio_anodizado":dat:=[A=25e-6*m_^2,L=1*m_,T1=600*K_,T2=400*K_,La=0.25*m_,T0=300*K_,h=20*W_/(m_^2*K_)];

Eqs. const.:

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

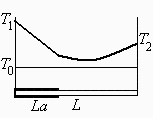
a) Hacer y explicar un esquema del perfil de temperaturas esperado.

La T máxima será 600 K, y la mínima entre 300 K y 400 K. Donde no hay convección, el perfil ha de ser recto, y donde sí la hay cóncavo.

b) Calcular la temperatura de la sección transversal central del tramo aislado.

Hay que resolver el problema coompleto. Sea Ta la temperatura al final de la funda (en x=La).

>

eqBE:=eq11_12;eqm:=eq11_13;eqBE1:=subs(m=0,eq11_14);T1x:=dsolve(eqBE1,T(x));eqBE2:=eq11_14;T2x:=dsolve(subs(T[infinity]=T0,eqBE2),T(x));eq0:='T1x(0)'=T1;eq1:='T1x(La)=T2x(La)';eq3:='-k*A*Diff(T1x,x)[La]=-k*A*Diff(T2x,x)[La]';eq4:='T2x(L)'=T2;T1x:=rhs(dsolve({eqBE1,T(0)=T1,T(La)=Ta},T(x)));T2x:=rhs(dsolve({subs(T[infinity]=T0,eqBE2),T(L)=T2,T(La)=Ta},T(x)));eq:=subs(x=La,eval(-k*A*diff(T1x,x)=-k*A*diff(T2x,x)));Ta_:=solve(%,Ta);eqm_:=evalf(subs(p=4*sqrt(A),dat,eqm));Ta__:=evalf(subs(eqm_,dat,SI0,Ta_))*K_;eqsol1:=T(La/2)=(T1+Ta)/2;subs(dat,T(La/2)=(T1+Ta__)/2);

c) Calcular la temperatura de la sección transversal central de la varilla.

Corresponde al tramo no aislado. El perfil de temperatura es:

>	plot(subs(eqm_,dat,SI0,{[x,subs(Ta=Ta__,T1x),x=0..La],[x,subs(Ta=Ta__,T2x),x=La..1]}),x=0..1,T=0..600,color=black,axes=BOXED,thickness=2);eqsol_c:=T(L/2)=evalf(subs(x=L/2,Ta=Ta__,eqm_,dat,SI0,T2x))*K_;

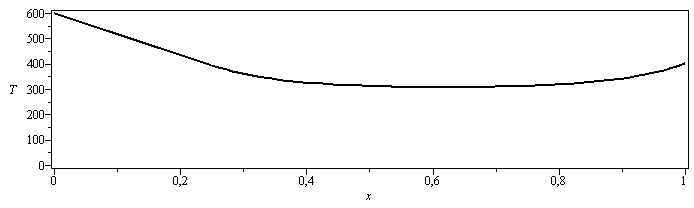d) Calcular la temperatura superficial mínima de la varilla y la posición en que se produce.

>	Q:=-k*A*diff(T(x),x);Q_:=simplify(subs(eqm_,Ta=Ta__,dat,SI0,-k*A*diff(T2x,x)));xQnull_:=solve(Q_=0,x)*m_;TQ0_:=evalf(subs(x=xQnull_,eqm_,Ta=Ta__,dat,SI0,T2x))*K_;

i.e., el mínimo tiene lugar a x=0,62 m y vale 307 K.

>