>	restart:#"m11_p48"

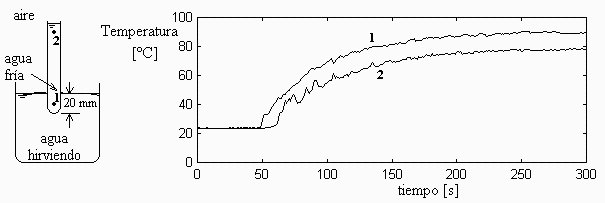
En la Fig. 1 se muestra el esquema de la instalación y el resultado del experimento siguiente. En un baño de agua hirviendo, se sumerge 2 cm un tubo de ensayo de 10 cm de altura, 10 mm de diámetro interior y 1 mm de espesor, de vidrio pyrex, lleno de agua del tiempo (dejando un par de milímetros libres para evitar el rebose en la dilatación). Se desea predecir dicho resultado esperimental con un modelo sencillo, para lo cual se pide:
a) A la vista del resultado, justificar las diferencias entre T1 y T2: a1) por qué arranca T2 después de T1, a2) por qué T1 no alcanza el punto de ebullición; a3) por qué el agua más caliente (que debería flotar) es la del fondo del tubo y no la de arriba.

b) Establecer el balance energético del agua del tubo en régimen transitorio y en estacionario, considerando que toda el agua del tubo tiene la misma temperatura (una media entre T1 y T2 en la figura) y despreciando el efecto de la superficie libre.
c) Representar esquemáticamente los flujos de calor de entrada y de salida del tubo, y calcular el flujo de calor por unidad de área a través del vidrio al principio. Para ello, tómense los valores orientativos: 20 W/(m2·K) para la convección natural en aire, 500 W/(m2·K) para la convección natural en el agua del tubo y 3000 W/(m2·K) para el agua hirviendo.

d) Establecer la transmisión de calor estacionaria a través de todo el vidrio (despréciese el efecto de la superficie libre), para determinar la temperatura media del agua del tubo.
e) Estimar el tiempo que tardaría en alcanzarse el régimen estacionario como cociente entre el calor necesario y el flujo de calor inicial, y compararlo con el resultado experimental.

Fig. 1. Perfil de temperaturas durante el ensayo de inmersión parcial del tubo con agua.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":su2:="Vidrio_pyrex":dat:=[Lw=0.020*m_,L=0.10*m_,D=0.01*m_,Le=1e-3*m_,T0=(24+273)*K_,ha=20*W_/(m_^2*K_),hw=500*W_/(m_^2*K_),hb=3000*W_/(m_^2*K_)];

Esquema:

>

Eqs. const.:

>	dat:=op(dat),get_liq_data(su1),Const,SI2,SI1:Vdat:=get_sol_data(su2);

a) A la vista del resultado, justificar las diferencias entre T1 y T2: a1) por qué arranca T2 después de T1, a2) por qué T1 no alcanza el punto de ebullición; a3) por qué el agua más caliente (que debería flotar) es la del fondo del tubo y no la de arriba.

a1) Arranca después porque tarda más tiempo en llegar el calor.

a2) El punto 1 no puede llegar a la temperatura del agua de fuera porque tiene un sumidero térmico hacia arriba, que está más frío. Por otra parte, hemos tomado la temperatura de ebullición igual a 100 ºC y el ensayo fue hecho en Madrid con agua hirviendo a 97 ºC, pero esto no es tan importante.

a3( El agua más caliente del fondo sí tiene flotabilidad y efectivamente se moverá hacia arriba, pero como se calienta por abajo y se enfría por arriba ha de ser T1>T2 para que se trasmita el calor.

b) Establecer el balance energético del agua del tubo en régimen transitorio y en estacionario, considerando que toda el agua del tubo tiene la misma temperatura (una media entre T1 y T2 en la figura) y despreciando el efecto de la superficie libre.

El agua del tubo recibe calor por abajo y cede calor por arriba.

>	eqBE:=DE=Q+W;eqBE:=m*c*dT/dt=Qin-Qout;eqBEstdy:=0=Qin-Qout;Q:=K*A*DT;K=1/(1/h[ext]+Le/kv+1/h[int]);eqBEstdy:=0=(1/(1/hb+Le/kv+1/hw))*A[wet]*(T[b]-T)-(1/(1/ha+Le/kv+1/hw))*A[dry]*(T-T0);

c) Representar esquemáticamente los flujos de calor de entrada y de salida del tubo, y calcular el flujo de calor por unidad de área a través del vidrio al principio. Para ello, tómense los valores orientativos: 20 W/(m2·K) para la convección natural en aire, 500 W/(m2·K) para la convección natural en el agua del tubo y 3000 W/(m2·K) para el agua hirviendo.

Tomamos T0=24 ºC a partir de la figura; si no, supondríamos T0=15 ºC.

>

qin_ini:=(1/(1/hb+Le/kv+1/hw))*(T[b]-T0);'1/hb,Le/kv,1/hw'=subs(dat,kv=k,Vdat,SI0,[1/hb,Le/kv,1/hw]);qout_ini:=0;qin_ini_:=subs(dat,kv=k,Vdat,dat,qin_ini):'qin_ini'=evalf(%,2);Qin_ini:=qin_ini*A[wet];A[wet]:=Pi*D^2/4+Lw*Pi*D;Awet_:=evalf(subs(dat,%)):'A[wet]'=evalf(%);Qin_ini_:=subs(dat,evalf(subs(kv=k,Vdat,Qin_ini)));

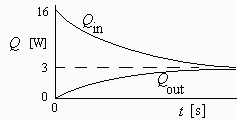
Se ve que la máxima resistencia térmica para la entrada de calor se da en el agua del tubo. Si sólo se hubiera considerado la resistencia en el vidrio el resultado sería unas 3 veces mayor. El efecto de la temperatura inicial del agua no es tan grande.

d) Establecer la transmisión de calor estacionaria a través de todo el vidrio (despréciese el efecto de la superficie libre), para determinar la temperatura media del agua del tubo.

>	A[dry]:=(L-Lw)*Pi*D;Adry_:=evalf(subs(dat,%)):'A[dry]'=evalf(%);eqBEstdy;eqBEstdy_:=(evalf(subs(dat,kv=k,Vdat,dat,eqBEstdy))):Tstdy_:=solve(%,T);'Tstdy'=evalf(TKC(Tstdy_));Qin_out:=subs(T=Tstdy_,dat,op(1,op(2,eqBEstdy_)));

i.e. el agua del tubo tenderá a alcanzar una temperatura media de unos 86 ºC, entrando 3 W por abajo y saliendo 3 W por arriba. Según los resultados experimentales se alcanzan unos 82 ºC de media, por lo que el modelo es razonablemente bueno para los coeficientes convectivos supuestos.

Nótese la pequeña influencia del vidrio en el estado estacionario, ya que si hacemos tender a 0 su espesor, la temperatura media del agua pasaría de 86 ºC a 89 ºC, transmitiéndose 3,2 W en vez de 3,0 W. En el caso límite de perfecta transmisión de calor en el vidrio y en el egua, i.e. sustituyendo el tubo con agua por una varilla de plata, se transmitirían 3,8 W (con la varilla a la temperatura de ebullición).

>

eqBEstdy__:=subs(Le=0,eqBEstdy);eqBEstdy_:=(evalf(subs(dat,kv=k,Vdat,dat,%))):Tstdy_:=solve(%,T);'Tstdy'=evalf(TKC(Tstdy_));Qin_out_:=subs(T=Tstdy_,dat,op(1,op(2,eqBEstdy_)));eqBEstdy__:=subs(Le=0,hb=1e9*hb,hw=1e9*hw,eqBEstdy);eqBEstdy_:=(evalf(subs(dat,kv=k,Vdat,dat,%))):Tstdy_:=solve(%,T);'Tstdy'=evalf(TKC(Tstdy_));Qin_out_:=subs(T=Tstdy_,dat,-op(2,op(2,eqBEstdy_)));

e) Estimar el tiempo que tardaría en alcanzarse el régimen estacionario como cociente entre el calor necesario y el flujo de calor inicial, y compararlo con el resultado experimental.
Suponemos que el agua del tubo se calentará casi hasta la temperatura de ebullición.

>	tc:=Qtotal/'Qin_ini';Qtotal:=mw*cw*(T[b]-T0);mw:=rho*L*Pi*D^2/4;mw_:=evalf(subs(dat,%)):'mw'=evalf(%,2);Qtotal_:=subs(cw=c,dat,mw_*cw*(T[b]-T0));tc_:=subs(dat,Qtotal_/Qin_ini_);

i.e. unos 150 s, que, pese a las grandes simplificaciones introducidas, se compara muy bien con el resultado experimental, que es lo que tarda en disminuir la diferencia hasta, digamos, un 5%, unos 200 s, o bien como el doble de lo que tarda en disminuir la diferencia hasta la mitad, 2x50=100 s, etc.

El haber despreciado la inercia térmica del vidrio es adecuado pese a que su masa es casi igual a la del agua, ya que su capacidad térmica es menor, y el contacto térmico mejor.

>	mv:=rho*Le*(Pi*D^2/4+L*Pi*D);mv_:=evalf(subs(Vdat,dat,%)):'mv'=evalf(%,2);eqCheck:=''mv*cv/(mw*cw)''=subs(cw=c,dat,cv=c,Vdat,dat,mv_*cv/(mw_*cw)):evalf(%,2);

i.e. el efecto del vidrio es aumentar un 20% la inercia térmica del conjunto.

En resumen, resulta bastante buena la suposición de temperatura uniforme en el agua del tubo, pues aunque ello signifique una resistencia térmica interna despreciable y en realidad sea finita, los efectos se compensan. Lo que habría sido un modelo inadecuado es suponer que la transmisión de calor en el agua del tubo era por conducción

COMENTARIOS ADICIONALES

Puede calcularse las temperaturas en las caras del vidrio en régimen estacionario.

Por la parte de abajo:

>	eq1:='Qin_out'=hb*Awet*(T[b]-Tv1);Tv1_:=subs(Awet=Awet_,dat,solve(eq1,Tv1));'Tv1_'=TKC(Tv1_);eq2:='Qin_out'=kv*Awet*(Tv1-Tv2)/Le;Tv2_:=subs(Tv1=Tv1_,Awet=Awet_,kv=k,Vdat,dat,solve(%,Tv2));'Tv2_'=TKC(Tv2_);

y por la parte de arriba:

>	eq4:='Qin_out'=ha*Adry_*(Tv4-T0);Tv4_:=subs(Adry=Adry_,dat,solve(%,Tv4));'Tv4_'=TKC(Tv4_);eq5:='Qin_out'=kv*Adry*(Tv3-Tv4)/Le;Tv3_:=subs(Tv4=Tv4_,Adry=Adry_,kv=k,Vdat,dat,solve(%,Tv3));'Tv3_'=TKC(Tv3_);

i.e. por abajo las 4 temperaturas del modelo son, hacia adentro: 100 ºC, 98,4 ºC, 94,2 ºC y los 86 ºC del agua por el interior, y por arriba son, hacia afuera: los 86 ºC del agua interior, 83,6 ºC, 82,4 ºC y los 24 ºC del aire exterior.

La variación longitudinal de temperatura en el vidrio, desde una media de (98,4 ºC+94,2 ºC)/2 abajo, hasta una media de (83,6 ºC+82,4 ºC)/2 arriba, apenas contribuiría a la transmisión de calor, pues el vidrio no es buen conductor y la sección de paso es pequeña. De todas formas, en la realidad la temperatura del vidrio variaría suavemente y no bruscamente de 96,3 ºC abajo a 83,0 ºC arriba.

>