>	restart:#"m11_p46"

Considérese el estado casi-estacionario de la transmisión de calor en un vaso cilíndrico de 30 mm de radio exterior, 2 mm de espesor de vidrio, y 160 mm de altura, conteniendo 200 cm3 de agua a 85 ºC en aire a 25 ºC. Se pide:
a) Determinar las temperaturas interior y exterior del vidrio tomando unos coeficientes convectivos de 500 W/(m2∙K) y 10 W/(m2∙K), respectivamente.
b) Determinar el flujo de calor total a través de la pared lateral bañada.
c) Determinar la temperatura en el borde superior, aplicando la teoría de aletas a la lámina de vidrio no mojada, suponiendo un valor de 80 ºC en la raiz y el coeficiente convectivo dado anteriormente para el aire.
d) Determinar el flujo de calor total hacia la parte superior por el vidrio.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":su2:="Vidrio_crown":su3:="Aire":dat:=[r1=28e-3*m_,r2=30e-3*m_,L=0.160*m_,Vliq=200e-6*m_^3,T0=(85+273.15)*K_,T3=(25+273.15)*K_,h1=500*W_/(m_^2*K_),h2=10*W_/(m_^2*K_),Troot=(80+273)*K_];

Eqs. const.:

>	Wdat:=get_liq_data(su1):Sdat:=get_sol_data(su2):Adat:=get_gas_data(su3):dat:=op(dat),Const,SI2,SI1:'k'=subs(Sdat,k);

a) Determinar las temperaturas interior y exterior del vidrio tomando unos coeficientes convectivos de 500 W/(m2∙K) y 10 W/(m2∙K), respectivamente.

El problema es unidimensional, y puede suponerse plano debido al pequeño espesor.

>	eq1:=q=h1*(T0-T1);eq2:=q=k*(T1-T2)/(r2-r1);eq3:=q=h2*(T2-T3);eq123:=q=(T0-T3)/(1/h1+(r2-r1)/k+1/h2);sol1_:=subs(Sdat,dat,solve({eq1,eq2,eq3},{q,T1,T2}));T0=TKC(subs(dat,T0));'T1'=TKC(subs(sol1_,T1));'T2'=TKC(subs(sol1_,T2));T3=TKC(subs(dat,T3));

b) Determinar el flujo de calor total a través de la pared lateral bañada.

>	Alatwet:=2*Pi*r1*Lliq;Lliq:=Vliq/(Pi*r1^2);Lliq_:=subs(dat,Lliq);Alatwet_:=subs(dat,Alatwet);Qlatwet:='q*Alatwet';Qlatwet_:=subs(sol1_,dat,Qlatwet);

c) Determinar la temperatura en el borde superior, aplicando la teoría de aletas a la lámina de vidrio no mojada, suponiendo un valor de 80 ºC en la raiz y el coeficiente convectivo dado anteriormente para el aire.

>

eqAletas:=(T-Tinf)/(Troot-Tinf)=cosh(m*(L-z))/cosh(m*L);eqm:=m=sqrt(h*p/(k*A));h:=h2;p:=2*Pi*r1+2*Pi*r2;A:=2*Pi*r1*(r2-r1);eqm_:=evalf(subs(Sdat,dat,eqm));Ttip:=Tinf+(Troot-Tinf)/cosh(m*L);L=Ltot-Lliq;L_:=evalf(subs(dat,L-Lliq_));Tinf:=T3;Ttip_:=evalf(subs(eqm,L=L_,Sdat,dat,SI0,Ttip))*K_;'Ttip'=TKC(Ttip_);

>	plot([25,subs(L=L_,eqm,Sdat,dat,SI0,solve(eqAletas,T))-273],z=0..L_/m_,T_C=0..100,color=black);

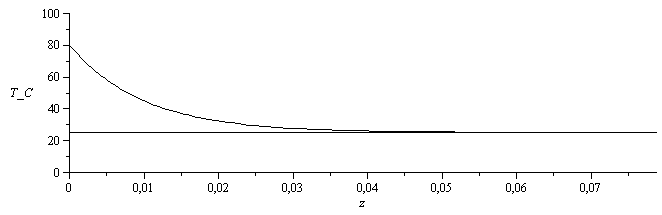d) Determinar el flujo de calor total hacia la parte superior por el vidrio.

>	eqAletas:=Qroot='m*k*A*(Troot-Tinf)*tanh(m*L)';eqAletas_:=Qroot=evalf(subs(L=L_,eqm,Sdat,dat,SI0,rhs(eqAletas)))*W_;

En resumen, salen 8 W por la pared lateral mojada (i.e. horizontalmente), y 2 W verticalmente hacia arriba por el vidrio. La pérdida de calor total sería la suma de esas dos más la del fondo más la de la superficie libre.

Se podría estimar el tiempo que tarda en enfriarse el agua (e.g. disminuir a la mitad los 60 ºC de diferencia con el ambiente), dividiendo la diferencia de energía interna por el flujo de calor:

>	tcool:=DH/Qdot;tcool:='m*c*(T0-T3)/(Qlatwet+Qroot)';tcool:=subs(dat,evalf(subs(eqAletas_,Wdat,dat,rho*Vliq*c*(T0-T3)/(Qlatwet_+Qroot))));

que resulta demasiado tiempo en la práctica.

La razón de esta discrepancia, y de otras, como la temperatura en el borde, que es mayor en la práctica, estriba en haber despreciado las pérdidas por arriba, y en la mala modelización de la transmisión en esa zona (parte interior del vaso no bañada por el agua). En realidad, el agua caliente genera vapor que se sobresatura y condensa en las paredes frías y en el aire frío, liberando bastante energía, así que el aire húmedo interior no está a la temperatura ambiente sino mucho más caliente (más cerca de la temperatura del agua que de la del aire exterior, en este caso de nivel profundo).

Un experimento de laboratorio en estas condiciones dio tcool=900 s hasta Tagua=55 ºC, y una Ttip=34 ºC (y si se tapa el vaso se llega a alcanzar 60 ºC en el borde).

>