>	restart:#"m11_p43"

Una varilla maciza de aluminio de 5 mm de diámetro y 25 cm de longitud, se ha doblado en U como se indica en la figura, quedando los extremos iguales de 5 cm de longitud, los cuales se sumergen en sendos baños de agua hirviendo y hielo fundente. La parte horizontal de la varilla se ha recubierto de una lámina de plástico de 1 mm de espesor y de conductividad 0,1 W/(m K), y se estima que el coeficiente de convección con el aire ambiente es de 10 W/(m2 K). Se pide:
a) Hacer sendos esquemas (axial y radial) de los perfiles de temperatura esperados, a lo largo de la varilla y transversalmente.
b) Para un elemento diferencial axial genérico de varilla de espesor dx, plantear el balance energético no estacionario.
c) Plantear la ecuación diferencial y las condiciones de contorno del problema estacionario, e indicar la solución.
d) Suponiendo despreciables las pérdidas al aire, calcular el gasto de hielo que irá fundiendo (se recogería para medirlo a través de una abertura no mostrada en la figura).  
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aluminio_anodizado":su2:="H2O":dat:=[D=0.005*m_,L=0.15*m_,T100=(100+273)*K_,T0=(0+273)*K_,Tinf=(15+273)*K_,DR=1e-3*m_,ka=0.1*W_/(m_*K_),h=10*W_/(m_^2*K_)];

Eqs. const.:

>	sdat:=get_sol_data(su1):dat:=op(dat),sdat,Const,SI2,SI1:Wdat:=get_liq_data(su2):

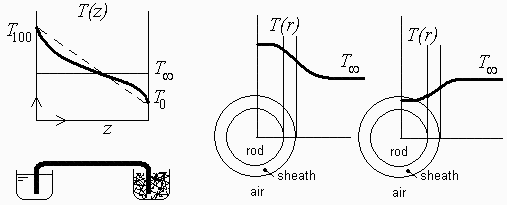
a) Hacer sendos esquemas (axial y radial) de los perfiles de temperatura esperados, a lo largo de la varilla y transversalmente.

Puede suponerse que los tramos sumergidos adquieren rápidamente la temperatura del baño porque la transmisin de calor es muy efectiva. El tiempo característico es t=rho*c*(D/4)/h=2700*900*(0,005/4)/1000=3 s.

Si no hubiese pérdidas laterales, en el régimen estacionario el perfíl axial de temperaturas sería lineal, y si hay transmisión lateral éste se rebajará un poco donde T>Tinf y subirá un poco donde T<Tinf.

El detalle de los perfiles radiales depende de si hay pérdidas o si hay ganancias laterales, pero en la práctica, la geometría hace que el problema pueda considerarse sólo axial (con fuentes o sumideros), i.e. T(x).

El tiempo caracterstico para que la varilla alcance el régimen, despreciando las pérdidas laterales) es t=rho*c*(L/2)^2/k=2700*900*(0,15/2)^2/200=70 s.

b) Para un elemento diferencial axial genérico de varilla de espesor dx, plantear el balance energético no estacionario.

Con el modelo unidimensional:

>	eqBE:=rho*A*dz*c*diff(T(z,t),t)=-k*A*diff(T(z,t),z)+k*A*(diff(T(z,t),z)+diff(T(z,t),z,z)*dz)+phi*dz;phi:=hm*pm*(T[inf]-T(z,t));eqBE:=collect(expand(eqBE),{dz,hm,pm});

donde hm y pm son los coeficientes h y p modificados por el efecto del aislante (aunque no interviene en los valores numéricos, al final se da su expresión explícita).

c) Plantear la ecuacin diferencial y las condiciones de contorno del problema estacionario, e indicar la solucin.

>	eqm:=m=sqrt(h*p/(k*A));A_:=subs(dat,Pi*D^2/4);p:=Pi*D;p_:=evalf(subs(dat,p));eqm_:=evalf(subs(p=p_,A=A_,dat,eqm));eqBEest:=0=diff(T(z),z,z)-m^2*(T(z)-Tinf);;eqCC1:=T(0)=T100;eqCC2:=T(L)=T0;

Esa ecuación diferencial tiene soluciones exponenciales (o hiperbólicas).

(Se ha representado la solución despreciando el efecto del aislante, i.e. con hm=h y pm=p).

>	sol:=collect(expand(convert(dsolve({eqBEest,eqCC1,eqCC2},T(z)),trig)),T100);plot(subs(eqm_,dat,SI0,[[[L,0],[L,100]],0,15,100,100*(1-z/L),rhs(sol)-273]),z=0..subs(dat,SI0,L),T=0..100,color=black);

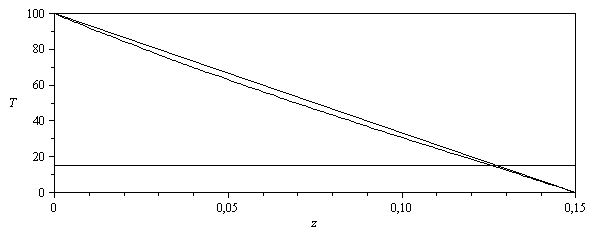¡Qué curioso!, cerca del extremo frío el perfil no sube sobre la solución lineal, como se había pensado. La explicación es que la Tinf está muy cercana; si estubiese a mitad (Tinf=50 ºC) el perfil deformado habría de ser antisimétrico respecto al punto medio.

d) Suponiendo despreciables las prdidas al aire, calcular el gasto de hielo que ir fundiendo (se recogera para medirlo a travs de una abertura no mostrada en la figura).  

Entonces el perfil de temperaturas es lineal, y el flujo de calor:

>	Qdot:=k*A*(T100-T0)/L;Qdot_:=subs(dat,evalf(subs(A=A_,dat,Qdot)));eqBEhielo:=mdot*hsl=Qdot;mdot_:=subs(Wdat,dat,Qdot_/h[sl0]);'mdot'=evalf(3600*mdot_*s_/h_);

i.e., en el estado estacionario se derritirían sólo 29 gramos/hora, que es muy poco y quedara enmascarado con la imperfección de los aislamientos.

Nota sobre los valores de hm y pm.

Del balance estacionario de energía a través del aislante:

>

eqQdot_trans:=Qdot=2*Pi*Rext*dz*hm*(Tinf-T(z));eqQdot_trans:=2*Pi*dx*ka*(T(z)-Te)/ln(Rext/Rint)=2*Pi*Rext*dz*h*(Te-Tinf);eq1:=1/hm=1/h+Rext*ln(Rext/Rint)/ka;eq2:=pm=2*Pi*Rext;Rext:=D/2+DR;hm_:=solve(subs(subs(Rint=D/2,dat,eq1)),hm);eq2_:=subs(dat,eq2):evalf(%,2);mm:='sqrt(pm*hm/(k*A))';mm_:=evalf(subs(dat,sqrt(((Pi*D+2*Pi*DR)*hm_)/(k*Pi*D^2/4))));

i.e. el efecto del aislante de plástico es disminuir el coeficiente de convección aparente de 10 W/(m2 K) a 8.9 W/(m2 K) (un 11%), pero aumentando el perímetro bañado de 16 a 22 mm (un 37), con lo que en total se aumentan las pérdidas pese a poner el aislante (el coeficiente m pasa del valor sin aislante de m=6.2 1/m al valor 7.0 1/m).

>