>	restart:#"m11_p42"

Considérese un cable eléctrico de aluminio, de 300 mm2 de sección, con una disipación térmica por efecto Joule uniforme en toda su sección. El cable esta protegido con un aislante de 4,5 mm de espesor y 0,05 W/(m·K) de conductividad térmica, cuyas temperaturas interior y exterior, en régimen estacionario, se miden y son de 90 ºC y 30 ºC. Se pide:

a) Hacer un esquema del perfil de temperaturas esperado.
b) Establecer el balance energético para un elemento tubular genérico de aislante (de espesor diferencial y longitud unitaria).
c) Establecer el balance energético para un elemento tubular genérico del cable de aluminio (de espesor diferencial y longitud unitaria).
d) Potencia disipada por unidad de longitud y temperatura en el eje.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(r>0,R1>0,R2>0):

>	su:="Aluminio_pulido":dat:=[A=300e-6*m_^2,DRais=4.5e-3*m_,kais=0.05*W_/(m_*K_),T1=(90+273)*K_,T2=(30+273)*K_];

Eqs. const.:

>	Sdat:=get_sol_data(su):dat:=op(dat),Sdat,Const,SI2,SI1:

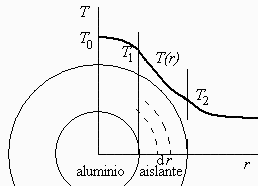
a) Hacer un esquema del perfil de temperaturas esperado.

En el eje ha de ser simétrico y sin gradiente (por no haber fuentes singulares en r=0). Ver arriba.

b) Establecer el balance energético para un elemento tubular genérico de aislante (de espesor diferencial y longitud unitaria)

>

eqBE:=dH/dt=Qdot_net;eqBE:=m*c*dT/dt=Q(r)-Q(r+dr);eqBE:=rho*2*Pi*r*dr*c*Diff(T,t)=-k*2*Pi*r*Diff(T,r)+k*2*Pi*(r+dr)*(Diff(T,r)+Diff(T,r,r)*dr);eqBE:=0=r*diff(T(r),r,r)+diff(T(r),r);eqT:=dsolve(eqBE,T(r));C1:=solve(T1=subs(r=R1,rhs(eqT)),_C1):C2:=solve(T2=subs(r=R2,_C1=C1,rhs(eqT)),_C2):eqT_:=simplify(subs(_C1=C1,_C2=C2,eqT));Q:=-k*2*Pi*r*diff(T(r),r);Q_:=eval(subs(eqT,_C2=C2,Q));R1:=sqrt(A/Pi);R1_:=evalf(subs(dat,SI0,R1))*m_:'R1'=evalf(%,2);R2='R1+DRais';R2_:=subs(dat,R1_+DRais);Q__:=evalf(subs(dat,-2*Pi*kais*(T2-T1)/ln(R2_/R1_))):'Q'=evalf(subs(SI0,%))*W_/m_;

i.e. en el aislante la temperatura disminuye hiperbólicamente. A su través fluyen 50 W/m.

c) Establecer el balance energético para un elemento tubular genérico del cable de aluminio (de espesor diferencial y longitud unitaria).

>

eqBE:=dH/dt=Qdot_net;eqBE:=m*c*dT/dt=Q(r)-Q(r+dr)+phi*V;eqBE:=rho*2*Pi*r*dr*c*Diff(T,t)=-k*2*Pi*r*Diff(T,r)+k*2*Pi*(r+dr)*(Diff(T,r)+Diff(T,r,r)*dr)+phi*2*Pi*r*dr;eqBE:=0=r*diff(T(r),r,r)+diff(T(r),r)+phi*r/k;eqT:=dsolve(eqBE,T(r));eqT0:=0=subs(r=R0,diff(rhs(eqT),r));eqT1:=T1=subs(_C1=0,r=R1,rhs(eqT));eqT_:=subs(_C1=0,_C2=solve(%,_C2),eqT);

i.e. la temperatura disminuye parabólicamente con el radio

d) Potencia disipada por unidad de longitud y temperatura en el eje.

Por continuidad del flujo de calor en r=R1:

>

eqQ1:=Qais=Qalu;eqQ1:=Qais='-k*2*Pi*R1*diff(T(r),r)';eqQ1_:=Qais=subs(_C1=0,r=R1,-k*2*Pi*R1*diff(rhs(eqT_),r));eqQs:=phi=solve(%,phi);eqQs_:=evalf(subs(Qais=Q__,dat,%)):'phi'=evalf(rhs(subs(SI0,%)),2)*W_/m_^3;eqT0:=evalf(subs(r=0,eqQs_,dat,eqT_)):evalf(%,4);DT01:=T1-T0;DT01_:=subs(dat,T1-rhs(eqT0));

i.e. la temperatura en el cable de aluminio puede considerarse uniforme en toda su sección.

>